目录
3777. 砖块 - 递推
1208. 翻硬币 - 递推
95. 费解的开关 - 递推 + 位运算
3777. 砖块 - 递推
3777. 砖块 - AcWing题库
题目:
思路:
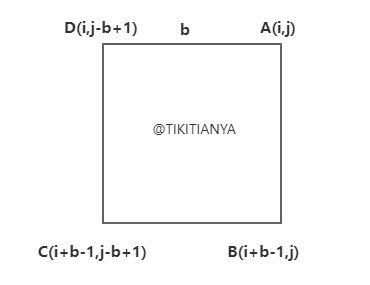
要使所有砖块颜色一致,则要不全B,要不全W
则分情况讨论:全为白色和全为黑色
- 全W:遍历1——n-1个砖块,如果遇到黑色砖块i,则将i和i+1的砖块颜色翻转
- 全B:遍历1——n-1个砖块,如果遇到白色砖块i,则将i和i+1的砖块颜色翻转
- 如果第n个砖块在全W情况不是白色且在全B情况不是黑色,说明无法使所有砖块颜色一致,输出-1
- 如果全W情况,最后一个砖块是白色,说明可以
- 如果全B情况,最后一个砖块是黑色,说明可以
import java.util.*;
class Main
{
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in);
int q=sc.nextInt();
while(q-->0)
{
int n=sc.nextInt();
String ss=sc.next();
char[] s=ss.toCharArray();
String tt=ss;
char[] t=tt.toCharArray();
int wres=0,bres=0;
List<Integer> res1=new ArrayList<>(),res2=new ArrayList<>();
for(int i=0;i<n-1;i++)
{
//变成全为白的情况
if(s[i]=='B')
{
s[i]='W';
if(s[i+1]=='B') s[i+1]='W';
else s[i+1]='B';
res1.add(i+1);
wres++;
}
//变成全为黑的情况
if(t[i]=='W')
{
t[i]='B';
if(t[i+1]=='W') t[i+1]='B';
else t[i+1]='W';
res2.add(i+1);
bres++;
}
}
if(s[n-1]=='B'&&t[n-1]=='W') System.out.println(-1);
else if(s[n-1]=='W')
{
System.out.println(wres);
for(int x:res1) System.out.print(x+" ");
if(wres!=0) System.out.println();
}else if(t[n-1]=='B')
{
System.out.println(bres);
for(int x:res2) System.out.print(x+" ");
if(bres!=0) System.out.println();
}
}
}
}
1208. 翻硬币 - 递推
活动 - AcWing
题目:
每次可以翻转两枚硬币
给出初始状态s1和需要达到的状态s2
求最少要多少次才能翻转成目标转态
思路:
因为题目保证一定有解
如果s1和s2在相同下标下正反不同,则翻转i和i+1的硬币,res+1
实际上,结果只要求输出最小翻转次数,因此每次只要翻转下一个硬币就可以了
import java.util.*;
class Main
{
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in);
String s=sc.next();
String t=sc.next();
char[] s1=s.toCharArray();
char[] s2=t.toCharArray();
int cnt=0;
for(int i=0;i<s.length()-1;i++)
{
if(s1[i]!=s2[i])
{
if(s1[i+1]=='*') s1[i+1]='o';
else s1[i+1]='*';
cnt++;
}
}
System.out.print(cnt);
}
}
95. 费解的开关 - 递推 + 位运算
活动 - AcWing
题目:
25盏灯排成一个 5×5 的方形。
每一个灯都有一个开关,游戏者可以改变它的状态。
每一步,游戏者可以改变某一个灯的状态。
游戏者改变一个灯会产生连锁反应:和这个灯上下左右相邻的灯也要相应地改变其状态。
我们用数字 1 表示一盏开着的灯,用数字 0 表示关着的灯。
给定一些游戏的初始状态,判断游戏者是否可能在 6 步以内使所有的灯都变亮
- 如果在6步以内可以完成,输出最小步数
- 如果无法在6步内完成,输出-1
思路:
枚举第0行的灯泡开关情况,00000~11111一共
种情况
通过第0行可以递归推出第1、第2……第4行的情况
也就是说一共有32种方案,在这些方案里求最小操作数即可
- 如果当前行状态已经确定,如果存在位置【i,j】开关为0,则要使这个开关为1,需要按下一行【i+1,j】的开关
- 注意:枚举32种情况时,都是对原方阵进行操作,所以需要用一个矩阵把原矩阵储存下来
- 当递推完0~3行开关后,若最后一行开关全为1,则表示成功,更新最小操作数
import java.util.*;
class Main
{
static int N=6;
static int[][] reg=new int[N][N];
static int[][] g=new int[N][N];
static int[] dx={0,-1,1,0,0},dy={0,0,0,-1,1};
public static void turn(int x,int y)
{
for(int i=0;i<5;i++)
{
int a=x+dx[i],b=y+dy[i];
if(a>=0&&a<=4&&b>=0&&b<=4) g[a][b]^=1;
}
}
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in);
int t=sc.nextInt();
while(t-->0)
{
int res=10;
//将测试样例原方阵存下来 因为要枚举32种情况 每次枚举的必须是原图
for(int i=0;i<5;i++)
{
String s=sc.next();
for(int j=0;j<5;j++)
reg[i][j]=s.charAt(j)-'0';
}
//枚举所有32种情况(00000~11111共2^5种情况)
for(int op=0;op<1<<5;op++)
{
int cnt=0; //记录翻转次数
//取出原矩阵
for(int i=0;i<5;i++)
for(int j=0;j<5;j++) g[i][j]=reg[i][j];
//对第0行开关进行操作(这里按1开关或按0都可以)
for(int i=0;i<5;i++)
if((op>>i&1)==0)
{
turn(0,i);
cnt++;
}
//递推出第1行到第4行的状态
//如果第i行为0,则需要通过按第i+1行的相应位置将其变成1
for(int i=0;i<4;i++)
for(int j=0;j<5;j++)
if(g[i][j]==0)
{
turn(i+1,j);
cnt++;
}
//检查最后一行看是否全亮
boolean f=true;
for(int i=0;i<5;i++)
if(g[4][i]==0) f=false;
if(f) res=Math.min(res,cnt);
}
if(res>6) res=-1;
System.out.println(res);
}
}
}




VRPTW常见求解算法--代码解析](https://img-blog.csdnimg.cn/7090a12c5a7e4083a2afc20e6a70d459.png)