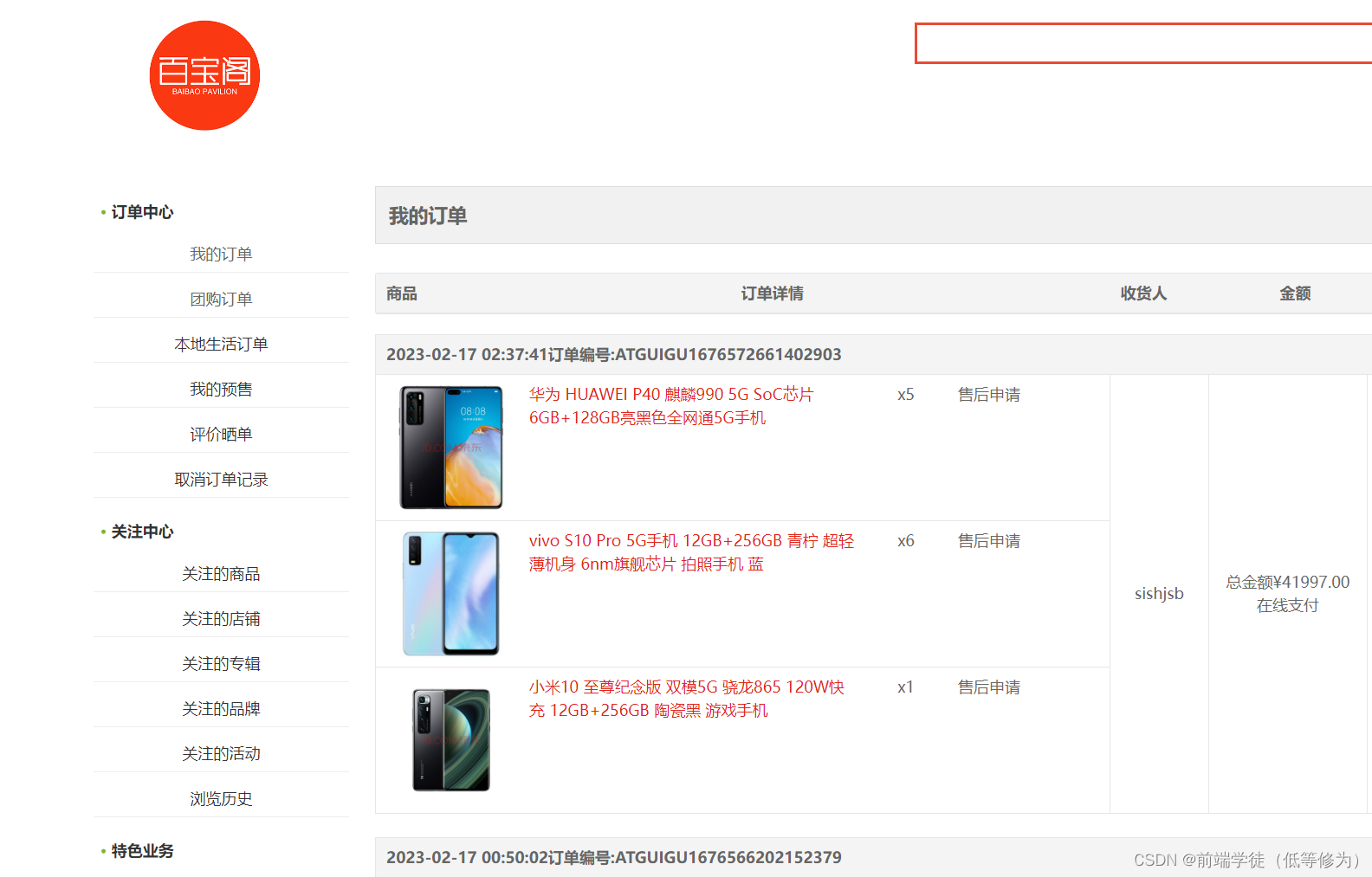
概念:
协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。协方差就是衡量两个变量相关性的变量。当协方差为正时,两个变量呈正相关关系(同增同减);当协方差为负时,两个变量呈负相关关系(一增一减)。
协方差性质:
协方差与方差之间有如下关系:
D(X+Y)=D(X)+D(Y)+2Cov(X,Y)
D(X-Y)=D(X)+D(Y)-2Cov(X,Y)
协方差与期望值有如下关系:
Cov(X,Y)=E(XY)-E(X)E(Y)。
协方差的性质:
(1)Cov(X,Y)=Cov(Y,X);
(2)Cov(aX,bY)=abCov(X,Y),(a,b是常数);
(3)Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)。
(4)Cov(a+X,b+Y)=Cov(X,Y)
由协方差定义,可以看出Cov(X,X)=D(X),Cov(Y,Y)=D(Y)。
举例:
Xi | 1.1 | 1.9 | 3 |
Yi | 5.0 | 10.4 | 14.6 |
E(X) = (1.1+1.9+3)/3=2
E(Y) = (5.0+10.4+14.6)/3=10
E(XY)=(1.1×5.0+1.9×10.4+3×14.6)/3=23.02
Cov(X,Y)=E(XY)-E(X)E(Y)=23.02-2×10=3.02


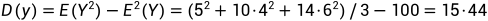

XY的相关系数:
r(X,Y)=Cov(X,Y)/(σxσy)=3.02/(0.77×3.93) = 0.9979
协方差矩阵:分别求出COV(XX),COV(YY),COV(XY)
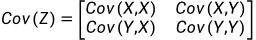
PCA求解过程:
主成分分析(Principal components analysis,以下简称PCA)是最重要的降维方法之一
PCA顾名思义,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。具体的,假如我们的数据集是n维的,共有m个数据(x(1),x(2),...,x(m))。我们希望将这m个数据的维度从n维降到n'维,希望这m个n'维的数据集尽可能的代表原始数据集。我们知道数据从n维降到n'维肯定会有损失,但是我们希望损失尽可能的小。
举例:
假设我们的数据集有10个二维数据(2.5,2.4), (0.5,0.7), (2.2,2.9), (1.9,2.2), (3.1,3.0), (2.3, 2.7), (2, 1.6), (1, 1.1), (1.5, 1.6), (1.1, 0.9),需要用PCA降到1维特征。
首先我们对样本中心化,这里样本的均值为(1.81, 1.91),所有的样本减去这个均值向量后,即中心化后的数据集为(0.69, 0.49), (-1.31, -1.21), (0.39, 0.99), (0.09, 0.29), (1.29, 1.09), (0.49, 0.79), (0.19, -0.31), (-0.81, -0.81), (-0.31, -0.31), (-0.71, -1.01)。
现在我们开始求样本的协方差矩阵,由于我们是二维的,则协方差矩阵为:

求出的协方差矩阵为:

接下来我们求特征值:

求它的行列式:|A-入E|=0
(0.6165-入)(0.7165-入)-0.61544*0.61544=0;
求解入的值为特征值(0.0490833989, 1.28402771)
求解特征值对应的特征向量:
把特征入1值带入计算:
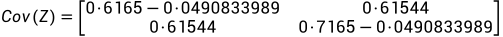
转化成行最简型:
可求出入1对应的特征向量为:
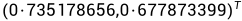
入2带入可求:

可求出入1对应的特征向量为:

我们原始数据集是二维的,降到1维,所以我们只需要找到最大的一个特征值对应的特征向量,就是我们所需要求解的w,最大特征值=1.28402771,特征向量w为
投影方程:
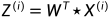
得到PCA降维后的10个一维数据集为:(-0.827970186, 1.77758033, -0.992197494, -0.274210416, -1.67580142, -0.912949103, 0.0991094375, 1.14457216, 0.438046137, 1.22382056)