全局空间自相关

空间自相关（spatial autocorrelation）是指一些变量在同一个分布区内的观测数据之间潜在的相互依赖性。Tobler(1970)曾指出“地理学第一定律：任何东西与别的东西之间都是相关的，但近处的东西比远处的东西相关性更强”

全局莫兰指数（Global Moran’s I）是最常用的空间自相关指数，用来反映全局的空间相关性，其计算公式为：

$$\begin{gathered} I= \\ fracNW \\ frac \\ sum\_i \\ sum\_j{w}_{ij}(x\_i- \\ barx)(x\_j- \\ barx) \\ sum\_i(x\_i- \\ barx{)}^2 \end{gathered}$$

式中，$N$表示空间单元的数量，$i$和$j$表示空间单元的位置索引，$x$为分析的变量，$barx$表示分析变量的均值，$w_{ij}$表示空间权重矩阵，$W$表示空间权重矩阵的和

Moran’s I大于0时，表示数据呈现空间正相关，其值越大空间相关性越明显；Moran’s I小于0时，表示数据呈现空间负相关，其值越小空间差异越大；Moran’s I为0时，空间呈随机性

解读莫兰指数的时候，需要有P值和Z得分来判定，P值小于0.05（通过95%置信度检验），且Z得分超过临界值1.65（拒绝零假设设定的阈值）

工具介绍

• PySAL是一个基于Python进行探索性空间数据分析的开放源码库，是由亚利桑那州立大学GeoDa Center for Geospatial Analysis and Computation赞助的社区项目

• libpysal：是Python空间分析库核心库，它提供了四个模块，构成了PySAL系列的空间分析工具：

  • 空间权重： libpysal.weights

  • 输入和输出：libpysal.io

  • 计算几何学：libpysal.cg

  • 内置示例数据集 libpysal.examples

• esda 是一个用于空间数据探索性分析的开放源码 Python 库，它是 PySAL (Python Spatial Analysis Library)的一个子包，包括全局和局部空间自相关分析的方法。

import esda  
import pandas as pd
import geopandas as gpd
from geopandas import GeoDataFrame
import libpysal as lps
import numpy as np
import matplotlib.pyplot as plt
from shapely.geometry import Point
import contextily as ctx
from pylab import figure, scatter, show
%matplotlib inline

root_dir="/root/learning/pysal/实验1/"
gdf = gpd.read_file(root_dir+'data/econ90040212.shp') # 读取数据

数据概况

gdf.columns.values  #字段名

array(['CODE', 'COUNT', 'SUM_AREA', 'FIRST_ANAM', 'OID_', 'CODE_1',
       'DATAFLAG', 'TOTPOP', 'TOTPOP_10K', 'RURPOP_10K', 'TOWNPOP_10',
       'AGRPRODUCT', 'AGRLBR_10K', 'AGRSTOTGDP', 'FSTGDPRATE',
       'SCNDGDPRAT', 'THRDGDPRAT', 'Province', 'geometry'], dtype=object)

gdf.head(1) # 查看一条记录

计算全局空间自相关指数Moran’s I

• 第一产业占GDP比重FSTGDPRATE为变量

ax=gdf.plot(figsize=(8,8),column="FSTGDPRATE")
ax.set_axis_off()

可以看出有一定的空间聚集性，但聚集性程度的大小需要通过Moran’s I的计算进一步衡量

计算空间权重矩阵

df = gdf
wq =  lps.weights.Queen.from_dataframe(df)# 使用Quuen式邻接矩阵
wq.transform = 'r' # 标准化矩阵

('WARNING: ', 98, ' is an island (no neighbors)')
('WARNING: ', 108, ' is an island (no neighbors)')
('WARNING: ', 137, ' is an island (no neighbors)')
('WARNING: ', 138, ' is an island (no neighbors)')
('WARNING: ', 139, ' is an island (no neighbors)')


/usr/local/lib/python3.6/dist-packages/libpysal/weights/weights.py:172: UserWarning: The weights matrix is not fully connected: 
 There are 6 disconnected components.
 There are 5 islands with ids: 98, 108, 137, 138, 139.
  warnings.warn(message)

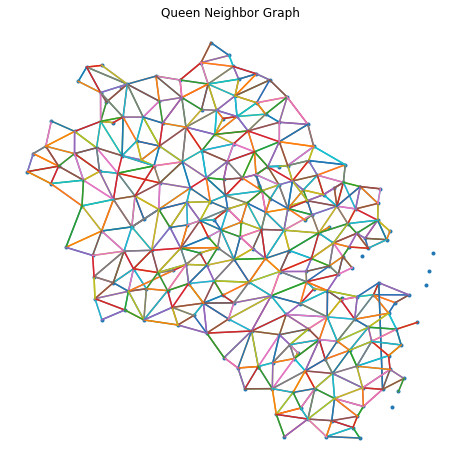
可以看到有5个单元没有邻接对象

接下来将计算得到的权重矩阵绘制出来进行观察

centroids = gdf.geometry.centroid # 计算多边形几何中心

fig = figure(figsize=(8,8))

plt.plot(centroids.x, centroids.y,'.')
for k,neighs in wq.neighbors.items():
    #print(k,neighs)
    origin = centroids[k]
    for neigh in neighs:
        segment = centroids[[k,neigh]]
        plt.plot(segment.x, segment.y, '-')
plt.title('Queen Neighbor Graph')
plt.axis('off')
plt.show()

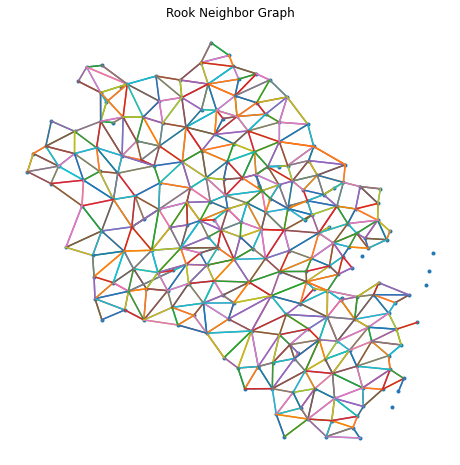
wr =  lps.weights.Rook.from_dataframe(df) # 使用Rook式邻接矩阵
# wr.transform = 'r' # 标准化矩阵

fig = figure(figsize=(8,8))

plt.plot(centroids.x, centroids.y,'.')
for k,neighs in wr.neighbors.items():
    #print(k,neighs)
    origin = centroids[k]
    for neigh in neighs:
        segment = centroids[[k,neigh]]
        plt.plot(segment.x, segment.y, '-')
plt.title('Rook Neighbor Graph')
plt.axis('off')
plt.show()

计算Moran’I

y=gdf["FSTGDPRATE"]
mi = esda.moran.Moran(y, wq)

print("Moran's I 值为：",mi.I)
print("随机分布假设下Z检验值为：",mi.z_rand)
print("随机分布假设下Z检验的P值为：",mi.p_rand)
print("正态分布假设下Z检验值为：",mi.z_norm)
print("正态分布假设下Z检验的P值为：",mi.p_norm)

Moran's I 值为： 0.7133088262106428
随机分布假设下Z检验值为： 16.7858372659958
随机分布假设下Z检验的P值为： 0.0
正态分布假设下Z检验值为： 16.826039087303325
正态分布假设下Z检验的P值为： 0.0

p<0.001，说明能够在99.9%的置信度下证明GDP中第一产业占比存在空间聚集性，空间相关性显著

绘制Moran’s I散点图

Moran散点图分为四个象限，分别表示四种局部空间相关关系:

• 第一象限（HH）：高值区被高值包围
• 第二象限（LH）：低值区被高值包围
• 第三象限（LL）：低值区被低值包围
• 第四象限（HL）：高值区被低值包围

from splot.esda import plot_moran
plot_moran(mi, zstandard=True, figsize=(10,4))
plt.show()

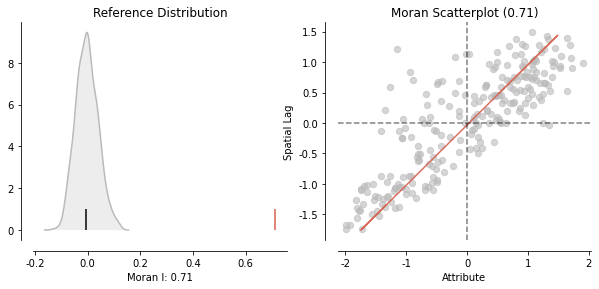
根据概率分布图，可以看出莫兰指数的值远大于大于随机正态分布的期望，这表明空间现象并不是随机分布的，而是具有一定相关性

根据散点图结果，可以看出全局Moran’s I 指数为0.708，并且大于0.5，因此其空间相关性较高

参考链接

• https://pysal.org/libpysal/
• https://pysal.org/esda/index.html
• https://github.com/pysal/esda
• http://pysal.org/notebooks/viz/splot/esda_morans_viz.html
• http://darribas.org/gds_scipy16/ipynb_md/04_esda.html
• https://splot.readthedocs.io/en/stable/users/tutorials/autocorrelation.html