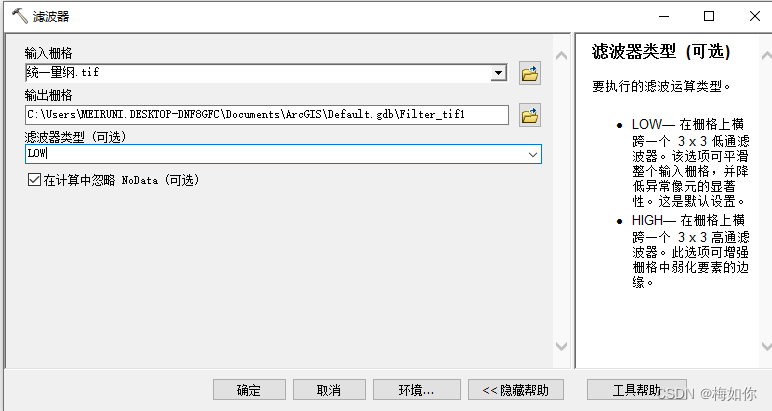
HMM模型 :

from hmmlearn.hmm import GaussianHMM
model= GaussianHMM(n_components=3,n_iter=100000, covariance_type = 'diag')
model.fit(X)

---

1、马尔科夫链

有向图模型（贝叶斯网络）：用有向图表示变量间的依赖关系；
无向图模型（马尔可夫网）：用无向图表示变量间的相关关系。
HMM 就是贝叶斯网络的一种--虽然它的名字里有和"马尔可夫网"一样的马尔可夫。
对变量序列建模的贝叶斯网络又叫动态贝叶斯网络。HMM 就是最简单的动态贝叶斯网络。
注意，马尔可夫过程其原始模型是马尔可夫链。该过程具有如下特性：在已知系统当前状态的条件下，它未来的演变不依赖于过去的演变。
也就是说，一个马尔可夫过程可以表示为系统在状态转移过程中，第 T+1 次结果只受第 T 次结果的影响，即只与当前状态有关，而与过去状态，即与系统的初始状态和此次转移前的所有状态无关。

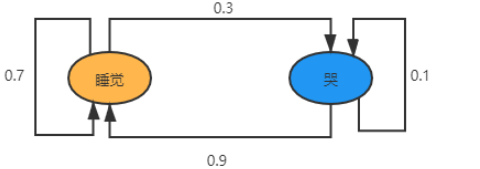
上图就是一个非常简单的马尔可夫链。两个节点分别表示睡和哭。边表示节点之间的转移概率。
睡之后，0.7 的可能又接着睡，只有 0.3 的可能变成哭。而哭之后，0.9 的可能是睡，也就有 0.1 的可能接着哭。
假设这是某个孩子的预报模型（这个孩子就只有哭和睡），则下一个状态只和上一个状态有关。和之前是在哭还是睡的状态没有关系。那么我们只要知道现在的状态，就可以推测接下来是睡还是哭的可能性了。
由马尔科夫链演化而成了隐含马尔可夫模型（Hidden Markov Model, HMM）！

2、HMM概述

2.1、HMM模型介绍

隐马尔科夫模型（Hidden Markov Model，以下简称HMM）是比较经典的机器学习模型了，它在语言识别，自然语言处理，模式识别等领域得到广泛的应用。
当然，随着目前深度学习的崛起，尤其是RNN，LSTM等神经网络序列模型的火热，HMM的地位有所下降。但是作为一个经典的模型，学习HMM的模型和对应算法，对我们解决问题建模的能力提高以及算法思路的拓展还是很好的。

2.2、HMM模型应用

首先我们来看看什么样的问题解决可以用HMM模型。
使用HMM模型时我们的问题一般有这两个特征：

• 我们的问题是基于序列的，比如时间序列，或者状态序列。
• 我们的问题中有两类数据，一类序列数据是可以观测到的，即观测序列；而另一类数据是不能观察到的，即隐藏状态序列，简称状态序列。

有了这两个特征，那么这个问题一般可以用HMM模型来尝试解决。这样的问题在实际生活中是很多的。比如：我现在在打字写博客，我在键盘上敲出来的一系列字符就是观测序列，而我实际想写的一段话就是隐藏序列，输入法的任务就是从敲入的一系列字符尽可能的猜测我要写的一段话，并把最可能的词语放在最前面让我选择，这就可以看做一个HMM模型了。再举一个，我在和你说话，我发出的一串连续的声音就是观测序列，而我实际要表达的一段话就是状态序列，你大脑的任务，就是从这一串连续的声音中判断出我最可能要表达的话的内容。

8、代码演练

8.1、参数估计问题

参数估计问题，也叫学习问题。已知观察序列，来对HMM模型的参数进行估计。

import numpy as np
# pip install hmmlearn
import hmmlearn.hmm as hmm

# 首先定义变量
status = ['盒子1', '盒子2', '盒子3']   # 隐藏的状态集合
obs = ['红球', '白球']     # 观察值集合，0==红球，1==白球
n_status = len(status)    # 隐藏状态的长度
# 初始概率分布： π 表示初次抽时，抽到1盒子的概率是0.2，抽到2盒子的概率是0.4，抽到3盒子的概率是0.4
pi = np.array([0.2, 0.4, 0.4])   

# 状态转移概率矩阵 A[0][0]=0.5 表示当前我抽到1盒子，下次还抽到1盒子的概率是0.5
A = np.array([[0.5, 0.2, 0.3],
              [0.3, 0.5, 0.2],
              [0.2, 0.3, 0.5]])
# 观测概率矩阵 B：B[2][0]=0.7,表示第三个盒子抽到红球概率0.7，B[2][1]=0.3，表示第三个盒子抽到白球概率0.3
B = np.array([[0.5, 0.5],
             [0.4, 0.6],
             [0.7, 0.3]])
# 下面开始定义模型
'''
hmmlearn中主要有两种模型，分布为：GaussianHMM和MultinomialHMM；
如果观测值是连续的，那么建议使用GaussianHMM，否则使用MultinomialHMM
参数：
初始的隐藏状态概率π参数为: startprob；
状态转移矩阵A参数为: transmat;
状态和观测值之间的转移矩阵B参数为: 
emissionprob_(MultinomialHMM模型中)或者在GaussianHMM模型中直接给定均值(means)和方差/协方差矩阵(covars)
'''
model = hmm.MultinomialHMM(n_components=n_status) # 隐藏状态长度
model.startprob_ = pi # 初始概率
model.transmat_ = A # 状态概率矩阵
model.emissionprob_ = B # 观测概率矩阵
# 观测序列[红、白、红]
se = np.array([[0,1,0]]).T

# 对数概率，index索引
logprob,box_index = model.decode(se,algorithm = 'viterbi')
print('隐藏状态盒子：')
print('  '.join(map(lambda t:status[t],box_index)))
print('最终计算的概率是：')
print(np.round(np.exp(logprob),4))

8.2、参数估计（训练问题）

已知观察序列，求什么样的隐藏状态序列最可能生成一个给定的观察序列

import numpy as np
# pip install hmmlearn
import hmmlearn.hmm as hmm

# 首先定义变量
status = ['盒子1', '盒子2', '盒子3']   # 隐藏的状态集合
obs = ['红球', '白球']     # 观察值集合，0==红球，1==白球
n_status = len(status)    # 隐藏状态的长度

# 观测数据
X_train = np.array([[0,1,0,1,0],# 第一次观测得到结果：红、白、红、白、红
                    [0,0,1,1,0],
                    [1,1,1,1,0],
                    [0,1,1,1,0],
                    [1,0,1,0,1]])

# 状态转移矩阵A？观察概率矩阵 B? 初始概率 Pi？
model = hmm.MultinomialHMM(n_components=n_status,n_iter=10,tol = 0.0001,
                           algorithm='viterbi')
model.fit(X_train)

# 查看模型估计的参数
# 概率问题，答案不是唯一的
print('初始概率是：',model.startprob_.round(5))
print('状态转移概率A：\n',model.transmat_.round(5))
print('观察概率矩阵B：\n',model.emissionprob_.round(5))

8.3、股票走势预测

8.3.1、加载数据

import numpy as np
import pandas as pd

from hmmlearn.hmm import GaussianHMM   # 股票的交易，数据每天都不一样，变化，连续数值
data = pd.read_csv('./apple_stock.csv') # 苹果公司，股票情况
print(data.shape)

data.head()

3.2  日期转换

data['Date'] = pd.to_datetime(data['Date'],format = '%Y/%m/%d',errors = 'ignore')
data.info()

3.3  数据提取

# 去除第一天的数据
volume = data['Volume'].values[1:] # 去除了交易额第一天的数据

close_v = data['Close'].values

# 前后两天股价数值的差值
diff = np.diff(close_v) # 涨、跌、平

X = np.column_stack([diff,volume])
X.shape

3.4  HMM算法建模

model= GaussianHMM(n_components=3,n_iter=100000, covariance_type = 'diag')

model.fit(X)

for i in range(model.n_components):# 模型的隐含状态：涨跌平
    print('第{0}个隐含状态'.format(i))
    print('平均值是：',model.means_[i])
    print('方差是：',np.diag(model.covars_[i]))
    print('------------------------------')

3.5  状态转移

print(model.transmat_.round(3))
'''
Transition matrix
[[0.898 0. 0.102]
[0. 0.915 0.085]
[0.083 0.043 0.874]]
'''

• 第一行最大的数值是0.915，因此跌倾向于保持自己的状态，即第二天仍旧为跌。
• 第二行最大的数值是0.898，得知涨后第二天倾向于变为涨。
• 根据第三行转变状态最大数值0.874，平后第二天仍旧倾向于平。