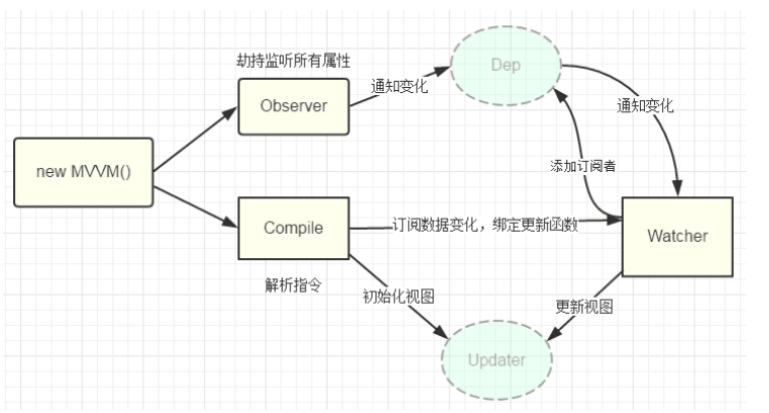
一、流程图

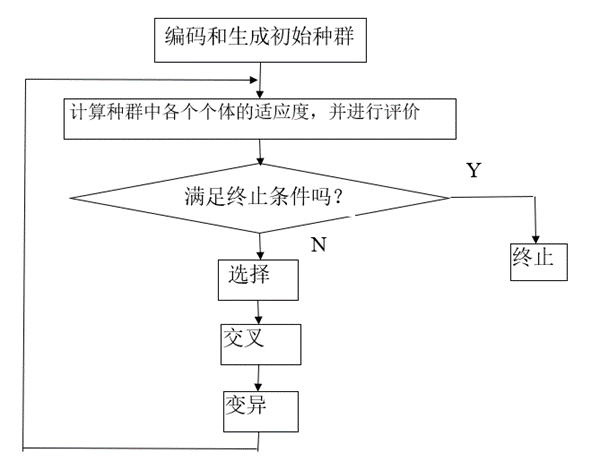
二、遗传编码

常用的遗传编码算法有霍兰德二进制码、格雷码、实数编码和字符编码等。我们这里只讲解二进制编码：

二进制编码是将原问题的结构变换为染色体的位串结构。在二进制编码中，首先要确定二进制字符串的长度 ，该长度与变量的定义域和所求问题的计算精度有关。

三、适应度函数

适应度函数是一个用于对个体的适应性进行度量的函数。通常，一个个体的适应度值越大，它被遗传到下一代种群中的概率也就越大。

3.1 常见的适应度函数

在遗传算吗中，有许多计算适应度的方法，其中最常用的适应度函数有以下两种：

3.1.1 原始适应度函数

采用原始适应度函数的优点是能够直接反映出待求解问题的最初求解目标，其缺点是有可能出现适应度值为负的情况。

3.1.2 标准适应度函数

四、基本遗传操作

遗传算法中的基本遗传操作包括选择、交叉和变异 种，而每种操作又包括多种不同的方法，下面分别对它们进行介绍。

4.1 选择操作

选择操作是指根据选择概率按照某种策略从当前种群中挑选出一定数目的个体，使它们能够有更多的机会被遗传到下一代中。常用的选择策略可分为比例选择、排序选择和竞技选择三种类型。

4.1.1 比例选择

比例选择方法的基本思想是：各个个体被选中的概率与其适应度大小成正比。

常用的比例选择策略包括轮盘赌选择和繁殖池选择。

4.1.2 轮盘赌选择

轮盘赌选择法又被称为转盘赌选择法或轮盘选择法。在这种方法中，个体被选中的概率取决于该个体的相对适应度。而相对适应度的定义为：

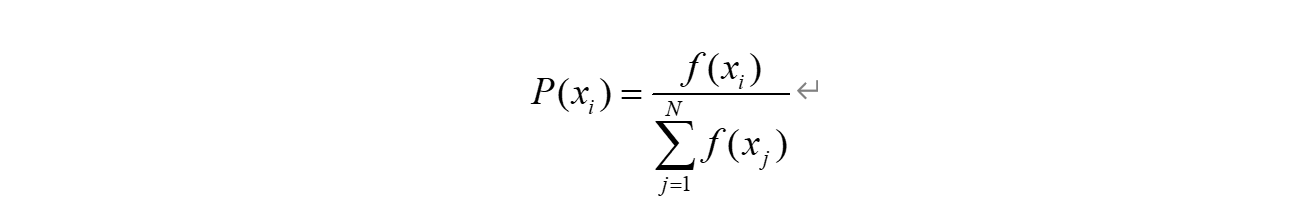
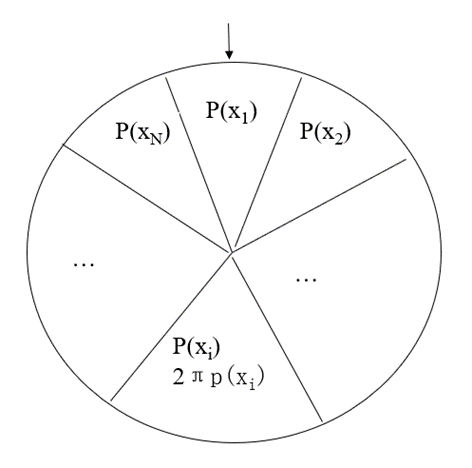
从统计角度看，个体的适应度值越大，其对应的扇区的面积越大，被选中的可能性也越大。这种方法有点类似于发放奖品使用的轮盘，并带有某种赌博的意思，因此亦被称为轮盘赌选择。

4.2 交叉操作

交叉操作是指按照某种方式对选择的父代个体的染色体的部分基因进行交配重组，从而形成新的个体。交配重组是自然界中生物遗传进化的一个主要环节，也是遗传算法中产生新的个体的最主要方法。根据个体编码方法的不同，遗传算法中的交叉操作可分为二进制交叉和实值交叉两种类型。

4.2.1 二进制交叉

二进制交叉是指二进制编码情况下所采用的交叉操作，它主要包括单点交叉、两点交叉、多点交叉和均匀交叉等方法。

4.2.2 单点交叉

单点交叉也称简单交叉，它是先在两个父代个体的编码串中随机设定一个交叉点，然后对这两个父代个体交叉点前面或后面部分的基因进行交换，并生成子代中的两个新的个体。假设两个父代的个体串分别是：

4.2.3 两点交叉

两点交叉是指先在两个父代个体的编码串中随机设定两个交叉点，然后再按这两个交叉点进行部分基因交换，生成子代中的两个新的个体。

假设两个父代的个体串分别是：

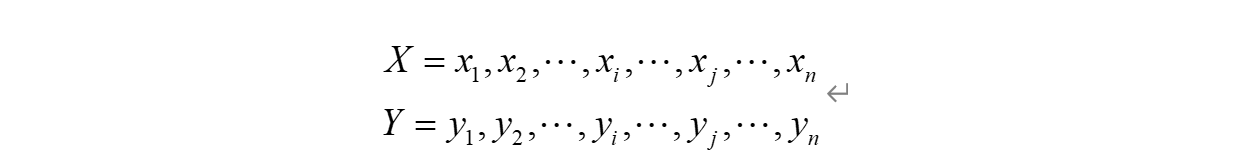
4.2.4 多点交叉

多点交叉是指先随机生成多个交叉点，然后再按这些交叉点分段地进行部分基因交换，生成子代中的两个新的个体。

这里不再赘述！

4.3 变异操作

变异是指对选中个体的染色体中的某些基因进行变动，以形成新的个体。变异也是生物遗传和自然进化中的一种基本现象，它可增强种群的多样性。遗传算法中的变异操作增加了算法的局部随机搜索能力，从而可以维持种群的多样性。根据个体编码方式的不同，变异操作可分为二进制变异和实值变异两种类型。

4.3.1 二进制变异

当个体的染色体采用二进制编码表示时，其变异操作应采用二进制变异方法。该变异方法是先随机地产生一个变异位，然后将该变异位置上的基因值由“0”变为“1”，或由“1”变为“0”，产生一个新的个体。

例：设变异前的个体为 0 0 1 1 0 1，若随机产生的变异位置是2，则该个体的第2位由“0”变为“1”。

三、遗传算法示例

按照遗传算法，求求解过程如下：

3.1 编码

3.2 生成初始种群

3.3 适应度函数

遗传算法中以个体适应度的大小来评定各个个体的优劣程度，从而决定其遗传机会的大小。

要计算个体的适应度，首先应该定义适应度函数。由于本例是求$f(x)$的最大值，因此可直接用$f(x)$来作为适应度函数。即：
$$f(s)=f(x)$$

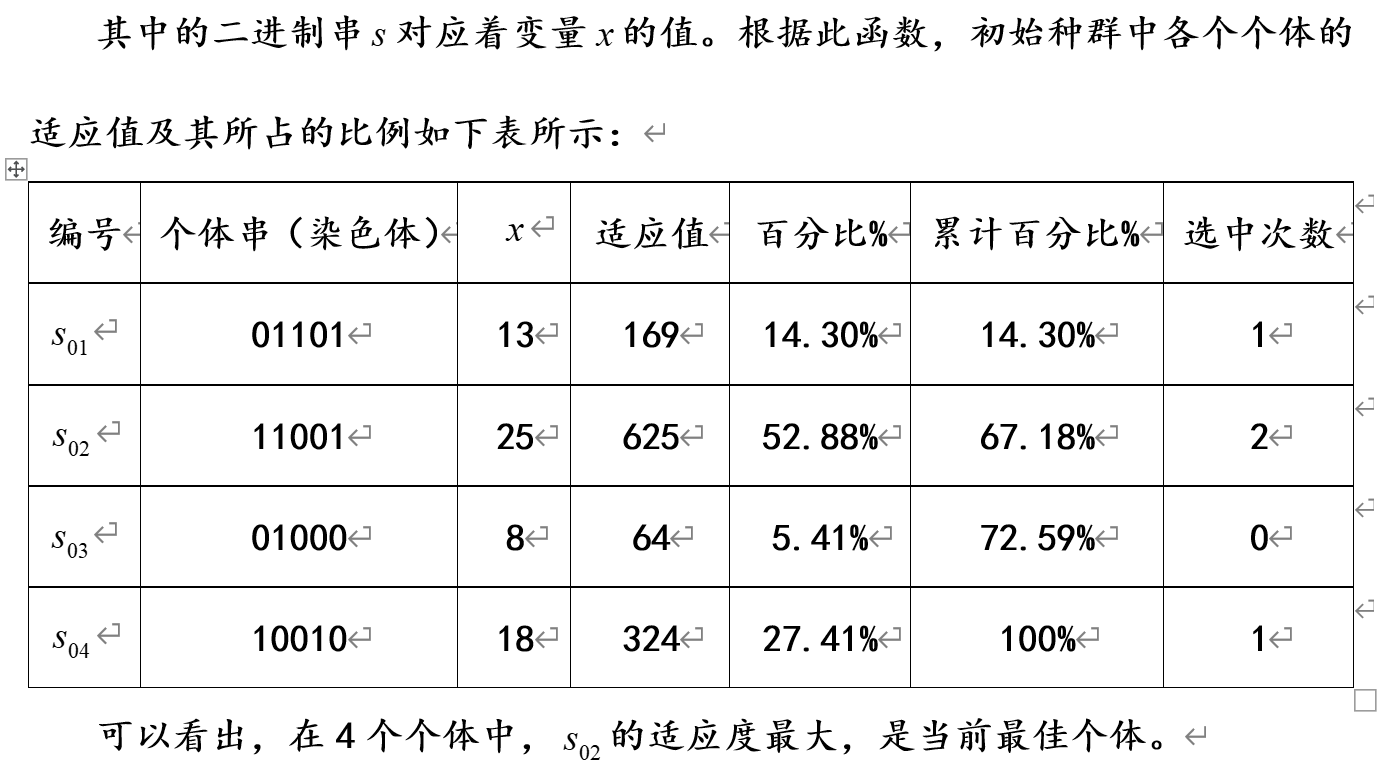
我总结为以下的几步：

3.4 选择操作

假设采用轮盘赌的方式选择个体，且依次生成的4个随机数（相当于轮盘上指针所指的数）为0.85、0.32、0.12、0.46，经选择后得到的新的种群为：

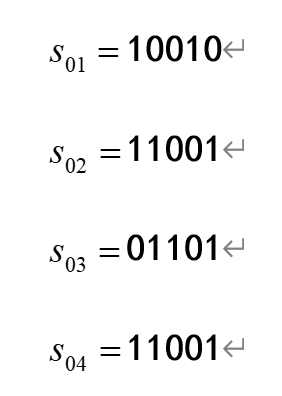
其中，染色体11001在种群中出现了2次，而原染色体01000则因适应值太小而被淘汰。

3.5 交叉

交叉运算是遗传算法中产生新个体的主要操作过程，它以某一概率相互交换某两个个体之间的部分染色体。

我总结为以下几步：

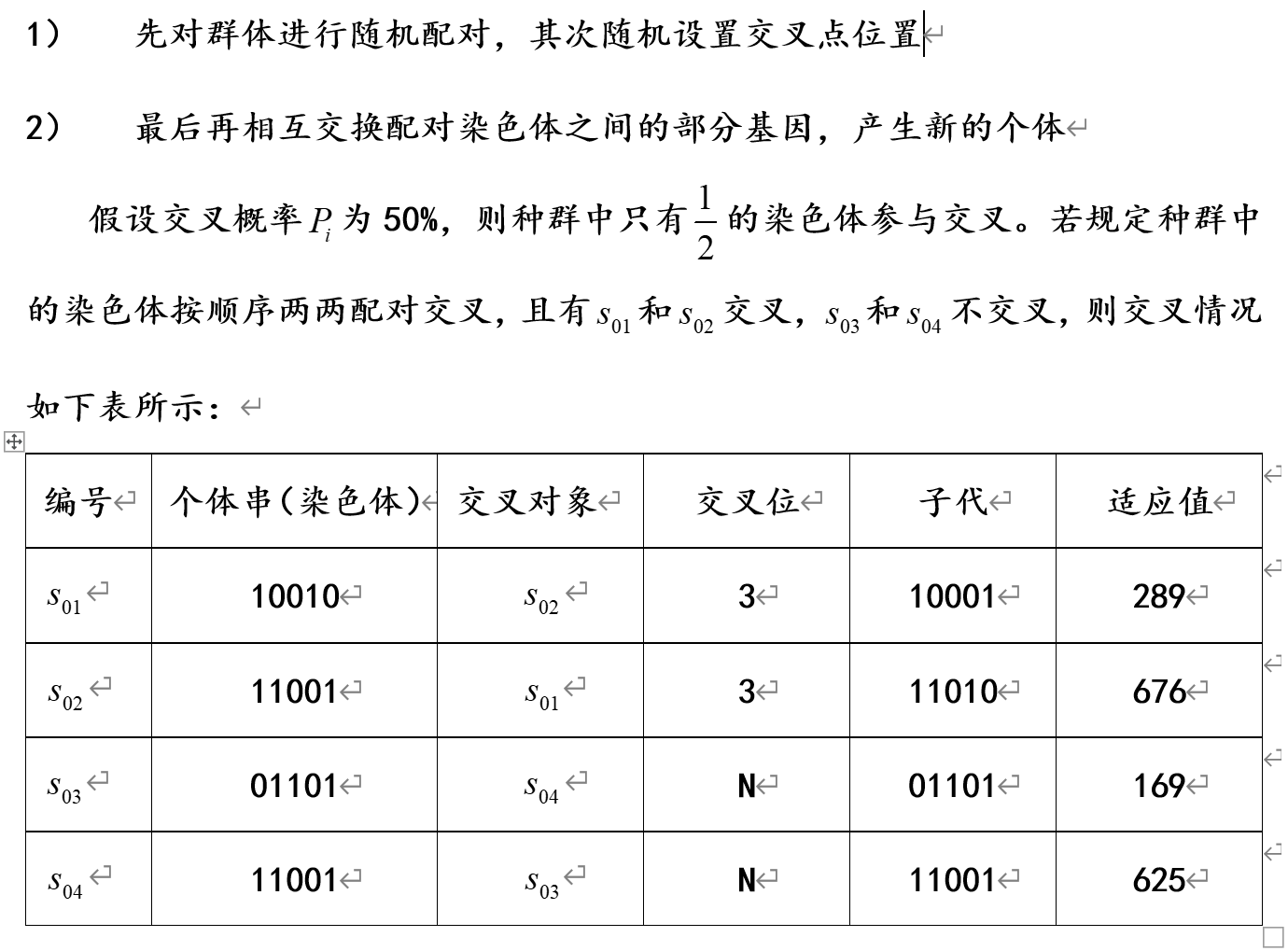
可见，经交叉后得到的新的种群为：

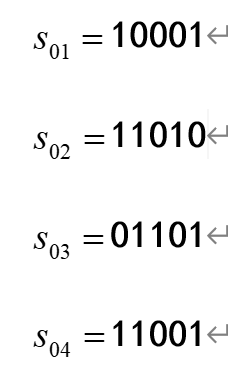
3.6 变异

变异运算是对个体的某一个或某一些基因座上的基因值按某一较小的概率进行改变，它也是产生新个体的一种操作方法。

总结：

然后，对第1代种群重复上述（4）—（6）的操作。

对第1代种群，同样重复上述（4）—（6）的操作，其选择情况如下所示：

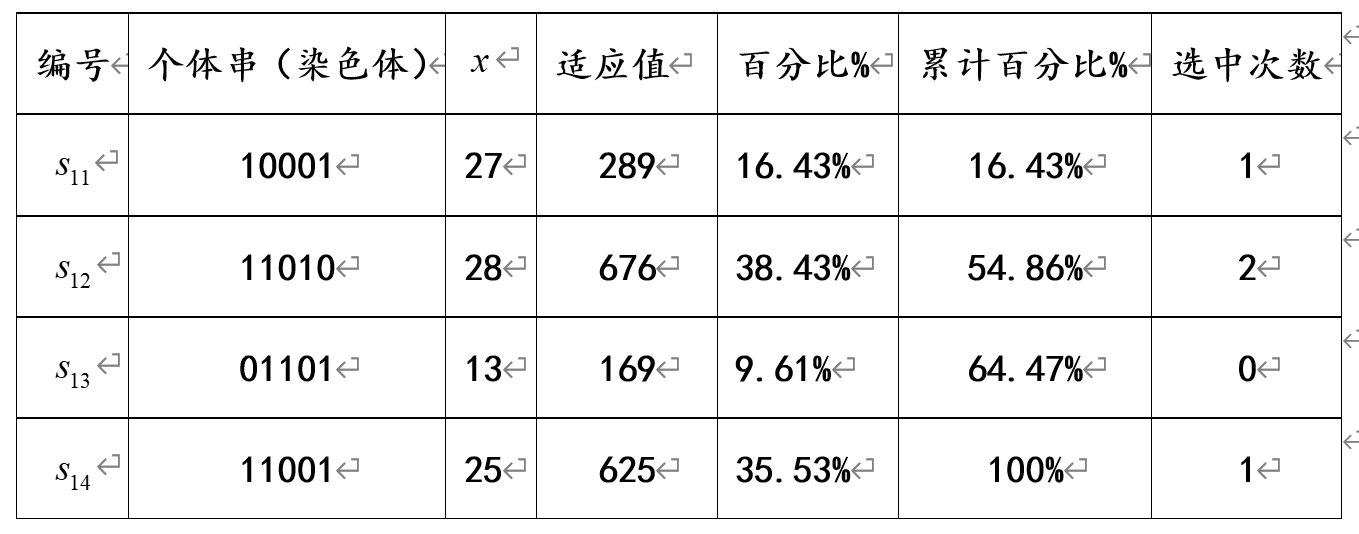
其中若假设按轮盘赌选择时依次生成的4个随机数为0.14、0.51、0.24和0.84，经选择后得到的新的种群为：

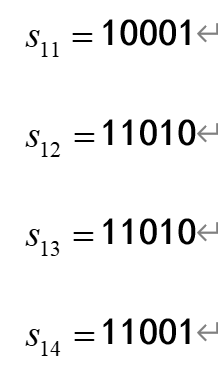
可以看出，染色体11010被选择了2次，而原染色体01101则因适应值太小而被淘汰。

对于第1代种群，其交叉情况如下表所示：

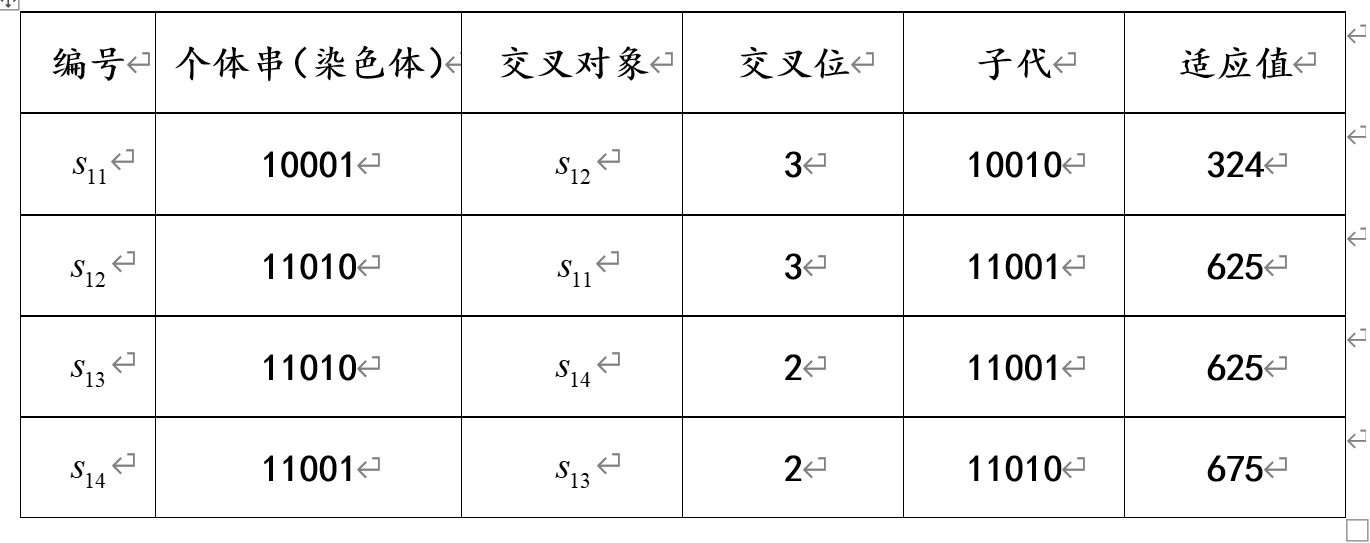
可见，经杂交后得到的新的种群为：

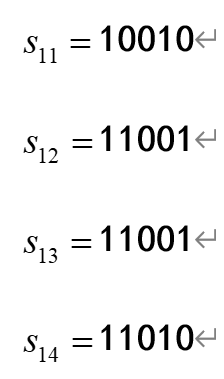
可以看出，第3位基因均为0，已经不可能通过交配达到最优解。这种过早陷入局部最优解的现象称为早熟。为解决这一问题，需要采用变异操作。

对于第一代种群，其变异情况如下表所示：

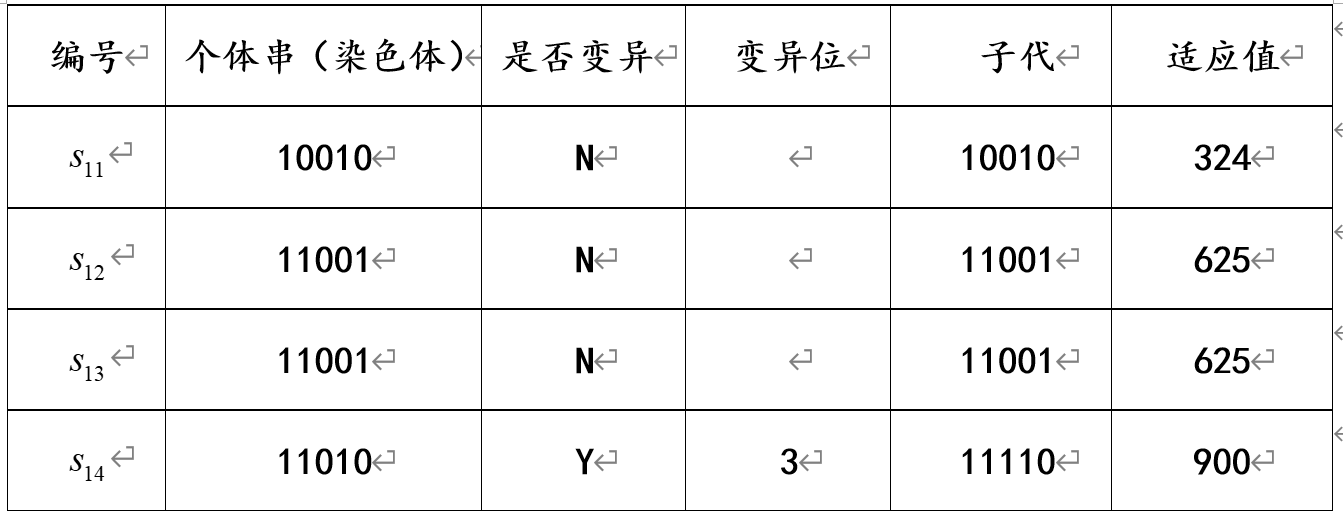
接着，再对第2代种群同样重复上述（4）—（6）的操作：

对第2代种群，同样重复上述(4)-(6)的操作。其选择情况如表所示：

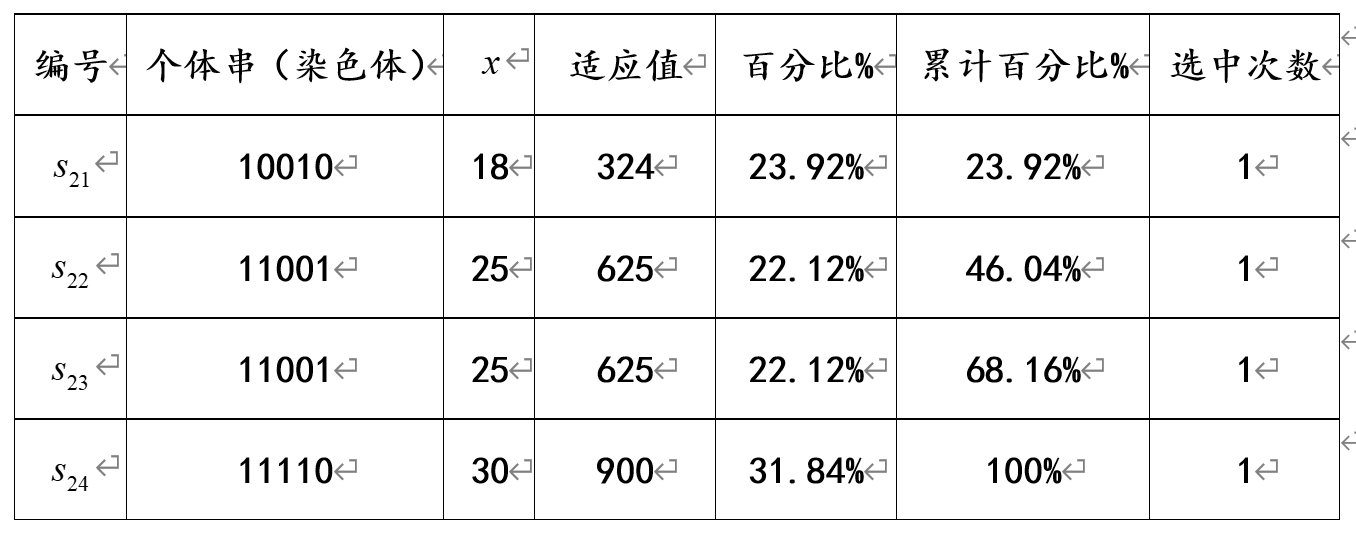
其中若假设按轮盘赌选择时依次生成的4个随机数为0.42、0.15、0.59和0.91，经选择后得到的新的种群为：

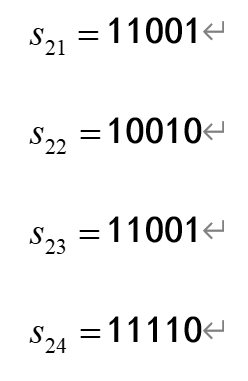
对第二代种群，其交叉情况如下表：

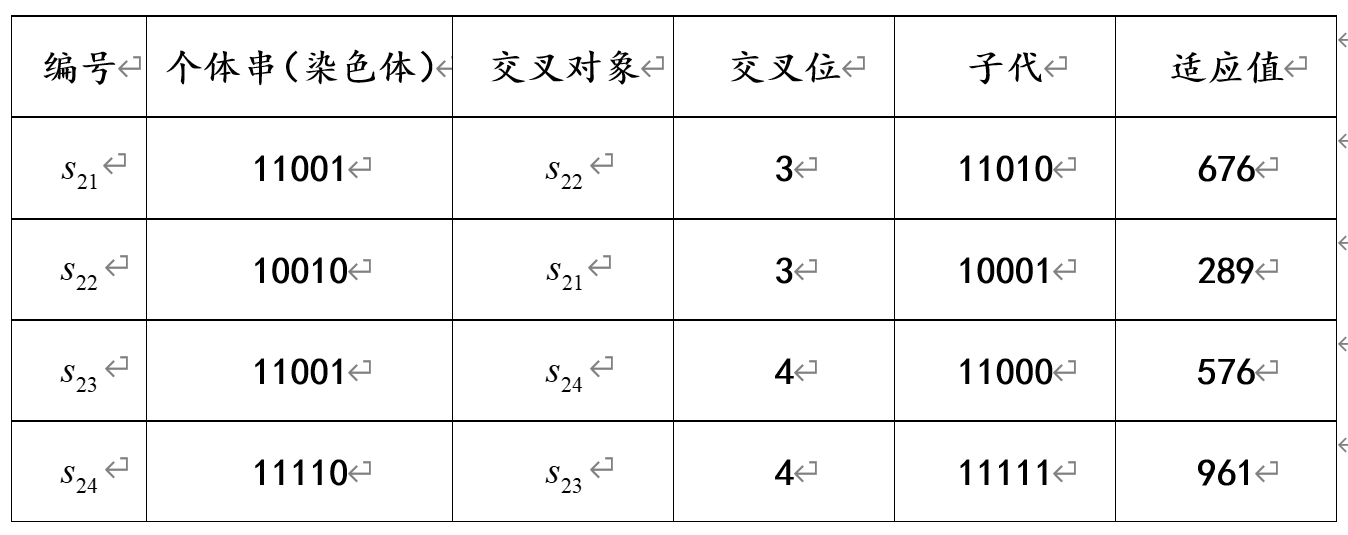
这时，函数的最大值已经出现，其对应的染色体为11111，经解码后可知问题的最优解是在点$x=31$处。