缩写：

SQP(Sequential Quadratic Programming)序列二次规划
NLP 非线性规划问题

matlab代码
matlab中求解器
SQP的认识
《最优化方法及其Matlab程序设计》 书 马昌凤

SQP 知乎

基础知识点

I.Jacobian矩阵
Def: 一阶偏导

II.Hessian矩阵
Def: 二阶偏导

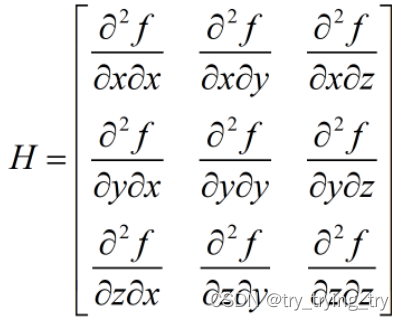
图 三阶的Hessian矩阵

意义:
二阶导数表示导数的变化规律，如果函数是一条曲线，且曲线存在二阶导数，那么二阶导数表示的是曲线的曲率，曲率越大，曲线越弯曲。以此类推，多维空间中的一个点的二阶导数就表示该点梯度下降的快慢。
e.g:$以二维图像为例，一阶导数是图像灰度的变化即灰度梯度，二阶导数就是灰度梯度变化程度，二阶导数越大灰度变化越不具有线性。（即灰度改变越大，不是线性的梯度。$ ）

0.前提知识-Newton method

牛顿法（Newton method）和拟牛顿法（quasi Newton method）是求解无约束最优化问题的常用方法，有收敛速度快的优点。
牛顿法是迭代算法，每一步都需求解目标函数的海塞矩阵（Hessian Matrix），计算比较复杂。
拟牛顿法通过正定矩阵近似海塞矩阵的逆矩阵或海塞矩阵，简化了这一计算过程。

I.求解方程的零值
原理

II.求解方程的极小值/最优化问题

III.小结
缺点：
1.Newton method迭代公式(*)没有步长因子，是定步长迭代.

2.

拟牛顿法：
基本思想是：不用二阶偏导数而构造出可以近似海塞矩阵（或海塞矩阵的逆）的正定对称阵。不同的构造方法就产生了不同的拟牛顿法。

reference：
知乎 牛顿法和拟牛顿法

1.SQP概念/理论

概念

非线性规划问题(NLP)
是目标函数或约束条件中包含非线性函数的规划问题。
一般说来，求解非线性规划问题比求解线性规划问题困难得多。而且，不像线性规划有单纯形法这一通用方法，非线性规划目前还没有适用于各种问题的一般算法，已有的各种方法都有其特定的适用范围。

序列二次规划算法(SQP)
是目前公认的求解约束非线性优化问题最有效的方法之一。
与其他算法相比，序列二次规划法的优点是收敛性好、计算效率高、边界搜索能力强，因此受到了广泛的重视及应用。
**思想：**在序列二次规划法的迭代过程中，每一步都需要求解一个或多个二次规划（QP）子问题。

二次规划问题(QP)
就是目标函数为二次函数，约束函数为线性函数的最优化问题。

缺点：
一般地，由于二次规划子问题的求解难以利用原问题的稀疏性、对称性等良好特性，随着问题规模的扩大，其计算工作量和所需存储量是非常大的。因此，目前的序列二次规划算法一般只适用与中小规模问题。

推导

SQP求解思想
将复杂的非线性约束最优化问题转化为比较简单的二次规划（QP）问题求解的算法。
QP求解思想
根据约束条件的不同，二次规划可分为等式约束二次规划问题和不等式约束二次规划问题。
[等式约束常见的解法有直接消去法、广义消去法、拉格朗日(Lagrange)法；
不等式约束基本思想是把不等式约束转化为等式约束再求解，常见解法有有效集(active set)方法，有效集方法在每步迭代中把有效约束作为等式约束，然后可以用拉格朗日法求解，重复直到求得最优解。]
PS:

数学过程：

Reference
SJTU分享 知乎
概念的辨析 详细

2.SQP matlab中工具

I.脚本命令
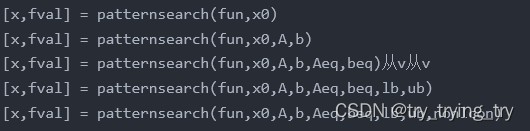
MathWorks -patternsearch
命令解释

参数解释：
％x为所求得的最小值点，而不是最小值
％fval为对应最小值点x处的最小值
％fun为目标函数。注：若有趣为m文件，要用通过句柄@进行引用
％x0 x0为给出进行搜索的初始向量
％A线性约束条件：不等式中的系数
％b线性约束条件：不等式右端的值
％Aeq线性约束条件：等式中的系数
％beq线性约束条件：等式右端的值
％lb x的下界
％ub x的上界

some说明：
模式搜索法（又称Hooke-Jeeves的算法）是一种直接搜索的算法，它并不依赖于导数，因此可以使用直接搜索来解决目标函数不可微分或甚至不连续的问题。
需要给定一个初始点.
MATLAB提供了三种直接搜索算法，称为广义模式搜索（GPS）法，生成集搜索（GSS）法和网格自适应搜索（MADS）法。它们的不同之处在于用于搜索的方向向量不同。

$\cdot$ example
①无约束

% function y = psobj(x)
% y = exp(-x(1)^2-x(2)^2)*(1+5*x(1) + 6*x(2) + 12*x(1)*cos(x(2)));
%存为psobj.m
fun=@psobj;
x0=[10,-10];
x=patternsearch(fun,x0)

②线性不等式约束

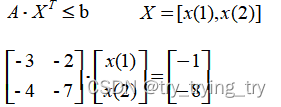
fun=@psobj;

A = [-3,-2;
    -4,-7];
b = [-1;-8];
x0 = [0.5,-0.5];
[x,fval] = patternsearch(fun,x0,A,b)

note:
A*x0 - b≥0, 初值要设在activate set区域

③边界限制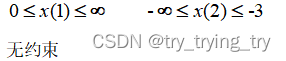

fun=@psobj;

lb = [0,-Inf];
ub = [Inf,-3];
A = [];
b = [];
Aeq = [];
beq = [];
x0 = [1,-5];
[x,fval] = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub)

④非线性约束

nonlinear inequalities c(x) or equalities ceq(x) defined in nonlcon.
patternsearch optimizes fun such that c(x) ≤ 0 and ceq(x) = 0.

function [c,ceq] = ellipsetilt(x)
% ceq = [];
% c = x(1)*x(2)/2 + (x(1)+2)^2 + (x(2)-2)^2/2 - 2;
%存为ellipsetilt.m

x0 = [-2,-2];
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = @ellipsetilt;
x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)

note:
c(x0)≥0 =8, 初值要设在activate set区域

===
命令的一些设置

① Different patternsearch Algorithms

x0 = 12*randn(1,2);
lb = [-15,-26];
ub = [26,15];
fun = @(x)sawtoothxy(x(1),x(2));

optsc = optimoptions("patternsearch",Algorithm="classic");%"nups"  "nups-mads"
[sol,fval,eflag,output] = patternsearch(fun,...
    x0,[],[],[],[],lb,ub,[],optsc)

②with Nondefault Options

fun=@psobj;

options = optimoptions('patternsearch','Display','iter','PlotFcn',@psplotbestf);  %酷，显示迭代细节
x0 = [0,0];
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
x = patternsearch(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

③Obtain All Outputs

[x,fval,exitflag,output] = patternsearch(fun,x0) 

缺点： 约束条件，多个方程时matrix提炼

===

II.GUI输入

缺点： 能否多个方程计算

意外收获
matlab 句柄函数求值

syms x y    %不能x(1) x(2)
f=@(x,y) x*y/2 + (x+2)^2 + (y-2)^2/2 - 2;
feval(f,-2,-2)