神经网络

题目背景

人工神经网络（Artificial Neural Network）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

题目描述

在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经元之间至多有一条边相连，下图是一个神经元的例子：

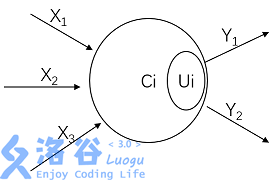
神经元〔编号为 $i$）

图中，$X_1\sim X_3$ 是信息输入渠道，$Y_1\sim Y_2$ 是信息输出渠道，$C_i$ 表示神经元目前的状态，$U_i$ 是阈值，可视为神经元的一个内在参数。

神经元按一定的顺序排列，构成整个神经网络。在兰兰的模型之中，神经网络中的神经元分为几层；称为输入层、输出层，和若干个中间层。每层神经元只向下一层的神经元输出信息，只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。

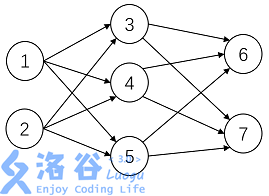
兰兰规定，$C_i$ 服从公式：（其中 $n$ 是网络中所有神经元的数目）

$$C_i=\left(\sum _{(j,i)\in E}{W}_{ji}{C}_j\right)-U_i$$

公式中的 $W_{ji}$（可能为负值）表示连接 $j$ 号神经元和 $i$ 号神经元的边的权值。当 $C_i$ 大于 $0$ 时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为 $C_i$。

如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。现在，给定一个神经网络，及当前输入层神经元的状态（$C_i$），要求你的程序运算出最后网络输出层的状态。

输入格式

输入文件第一行是两个整数 $n$（$1\le n\le 100$）和 $p$。接下来 $n$ 行，每行 $2$ 个整数，第 $i+1$ 行是神经元 $i$ 最初状态和其阈值（$U_i$），非输入层的神经元开始时状态必然为 $0$。再下面 $P$ 行，每行由 $2$ 个整数 $i,j$ 及 $1$ 个整数 $W_{ij}$，表示连接神经元 $i,j$ 的边权值为 $W_{ij}$。

输出格式

输出文件包含若干行，每行有 $2$ 个整数，分别对应一个神经元的编号，及其最后的状态，$2$ 个整数间以空格分隔。仅输出最后状态大于 $0$ 的输出层神经元状态，并且按照编号由小到大顺序输出。

若输出层的神经元最后状态均为 $0$，则输出 NULL。

样例

样例输入

5 6
1 0
1 0
0 1
0 1
0 1
1 3 1
1 4 1
1 5 1
2 3 1
2 4 1
2 5 1

样例输出

3 1
4 1
5 1

思路

这种结构就是拓扑排序，但有几个不会的点，需要记录边的权重，之前没用链接表存储边权。

代码实现

import java.util.*;

public class Main{
    static class edge{
        int to;
        // 边权
        int weight;
        // next指向下一个起始点当前i的边。
        int next;
        edge(int to, int weight, int next){
            this.to = to;
            this.weight = weight;
            this.next = next;
        }
    }
    static edge[] e = new edge[220];
    static int cnt = 0;
    static boolean[] vis = new boolean[105], out = new boolean[105];
    static int[] head = new int[105], in = new int[105], c = new int[105];

    static void add(int x, int y, int val){
        ++cnt;
        /
        e[cnt] = new edge(y, val, head[x]);
        head[x] = cnt;
    }

    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(), m = sc.nextInt();
        Queue<Integer> queue = new ArrayDeque<>();
        int u;
        for(int i = 1; i <= n; i++){
            c[i] = sc.nextInt();
            u = sc.nextInt();
            if(c[i] != 0){
                queue.offer(i);
                vis[i] = true;
            }else c[i] -= u;
        }
        int cur, next, val;
        for(int i = 1; i <= m; i++) {
            cur = sc.nextInt();
            next = sc.nextInt();
            val = sc.nextInt();
            add(cur, next, val);
            in[next]++;
            out[cur] = true;
        }
        while(!queue.isEmpty()){
            int x = queue.poll();
            if(c[x] < 0) continue;;
            for(int i = head[x]; i > 0; i = e[i].next){
                int y = e[i].to;
                --in[y];
                if(!vis[y] && in[y] == 0){
                    queue.offer(y);
                    vis[y] = false;
                }
                c[y] += c[x] * e[i].weight;
            }
        }
        boolean juege = true;
        for (int i = 1; i <= n; i++) {
            if(c[i] > 0 && !out[i]){
                System.out.println(i+" "+c[i]);
                juege =  false;
            }
        }
        if(juege) System.out.println("NULL");
        sc.close();
    }
}

统计特殊子序列的数目

题目描述

特殊序列 是由 正整数 个 0 ，紧接着 正整数 个 1 ，最后 正整数 个 2 组成的序列。

• 比方说，[0,1,2] 和 [0,0,1,1,1,2] 是特殊序列。
• 相反，[2,1,0] ，[1] 和 [0,1,2,0] 就不是特殊序列。
  给你一个数组 nums （仅 包含整数 0，1 和 2），请你返回 不同特殊子序列的数目 。由于答案可能很大，请你将它对 109 + 7 取余 后返回。

一个数组的 子序列 是从原数组中删除零个或者若干个元素后，剩下元素不改变顺序得到的序列。如果两个子序列的 下标集合 不同，那么这两个子序列是 不同的 。

样例

样例输入

nums = [0,1,2,2]
nums = [2,2,0,0]
nums = [0,1,2,0,1,2]

样例输出

3
解释：特殊子序列为 [0,1,2,2]，[0,1,2,2] 和 [0,1,2,2] 。

0
解释：数组 [2,2,0,0] 中没有特殊子序列。

7
解释：特殊子序列包括：
[0,1,2,0,1,2]
[0,1,2,0,1,2]
[0,1,2,0,1,2]
[0,1,2,0,1,2]
[0,1,2,0,1,2]
[0,1,2,0,1,2]
[0,1,2,0,1,2]

提示

• $1<=nums.length<=10^5$
• $0<=nums[i]<=2$

思路

还是动态规划，这个需要回答的大问题，可以化作多个相同类型的子问题进行回答，即可以使用动态规划。
思考动态规划时，还是可以先思考如何写出递归的解决方案。然后就能发现,状态转移方程式。

代码实现

class Solution {
    public int countSpecialSubsequences(int[] nums) {
        int MOD = (int)1e9 + 7;
        long[] dp = new long[3];
        for(int num : nums){
            if(num == 0) dp[0] = (2 * dp[0] + 1) % MOD;
            else if(num == 1) dp[1] = (dp[1] * 2 + dp[0]) % MOD;
            else dp[2] = (dp[2] * 2 + dp[1]) % MOD;
        }
        return (int)dp[2];
    }
}

矩阵中和能被 K 整除的路径

题目描述

给你一个下标从 0 开始的 m x n 整数矩阵 grid 和一个整数 k 。你从起点 (0, 0) 出发，每一步只能往 下 或者往 右 ，你想要到达终点 (m - 1, n - 1) 。

请你返回路径和能被 k 整除的路径数目，由于答案可能很大，返回答案对 109 + 7 取余 的结果。

样例

样例输入

grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3
grid = [[0,0]], k = 5
grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1

样例输出

2
解释：有两条路径满足路径上元素的和能被 k 整除。
第一条路径为上图中用红色标注的路径，和为 5 + 2 + 4 + 5 + 2 = 18 ，能被 3 整除。
第二条路径为上图中用蓝色标注的路径，和为 5 + 3 + 0 + 5 + 2 = 15 ，能被 3 整除。

1
解释：红色标注的路径和为 0 + 0 = 0 ，能被 5 整除。

10
解释：每个数字都能被 1 整除，所以每一条路径的和都能被 k 整除。

提示

• $m==grid.length$
• $n==grid[i].length$
• $1<=m,n<=5\ast 10^4$
• $1<=m\ast n<=5\ast 10^4$
• $0<=grid[i][j]<=100$
• $1<=k<=50$

思路

还是动态规划。

代码实现

class Solution {
    public int numberOfPaths(int[][] grid, int k) {
        int MOD = (int)1e9+7;
        int n = grid.length, m = grid[0].length;
        int[][][] dp = new int[n+1][m+1][k];
        // 初始化起点
        dp[0][1][0] = 1;
        for(int i = 0; i < n; i++)
            for(int j = 0; j < m; j++)
                for(int l = 0; l < k; l++)
                    dp[i+1][j+1][(l + grid[i][j]) % k] = (dp[i+1][j][l] + dp[i][j+1][l]) % MOD;
        return dp[n][m][0];
    }
}