论文题目
Learning Entity and Relation Embeddings for Knowledge Graph Completion
论文链接
TransR
文中指出,不管是TransE还是TransH都是将实体和关系映射同一空间,但是,一个实体可能具有多个层面的信息,不同的关系可能关注实体的不同层面。实体和关系表达的最佳维度并不一定是一致的,因此,映射到同一个空间可能会限制模型效果。
作者认为,两个实体在具有相似的意思时应该在实体空间中距离相近,在意思不相近时距离较远,比如(苹果,华为)都代表科技产品时候应该距离相近,在苹果表示水果是距离较远。
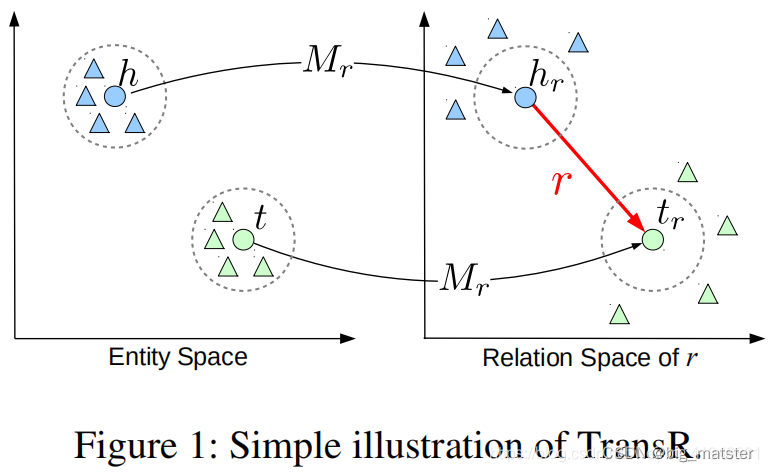
实体
h
h
h和
t
t
t通过
M
r
Mr
Mr矩阵映射到关系空间,分别为
h
r
hr
hr和
t
r
tr
tr,目标为
h
r
+
r
=
t
r
hr + r = tr
hr+r=tr
通过这个映射,与具有
r
r
r关系的实体变近,与不具有
r
r
r关系的实体距离变远。
文中还指出具有同一种关系的实体可能具有多种模式,对于位置包含关系,可能有可能有(国家,城市),(国家,大学)…各种,因此文中提出将具有同一种关系的实体对进行聚类
c
T
r
a
n
s
R
cTransR
cTransR模型
TransR
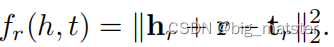
- 将其映射到不同空间,与TransE基本类似。
cTransR
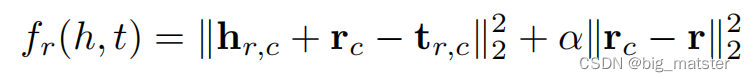

核心不同点,将实体和关系映射到不同空间。
论文中的讲解
Lin 等人[43]提出了 TransR,该方法在不同的空间(实体空间和关系空间)中对实体和关系进行建模,并在关系空间中进行翻译。
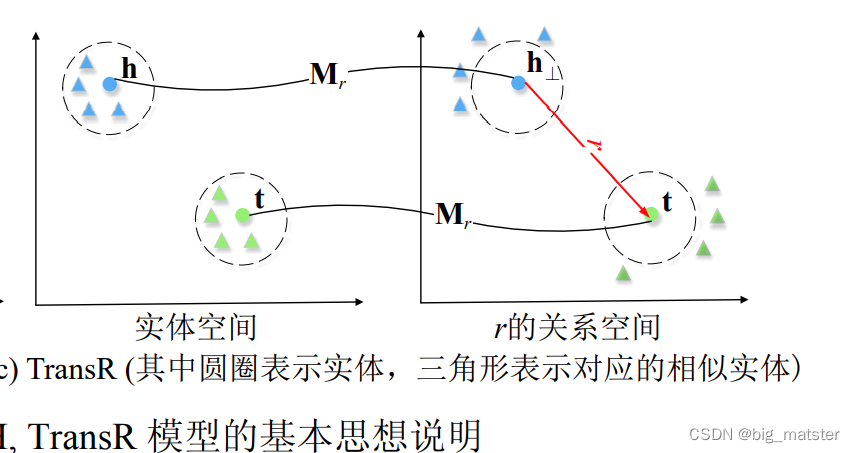
对于每个三元组
(
h
,
r
,
t
)
(h,r,t)
(h,r,t),首先将头尾实体向量,向关系
r
r
r空间投影。使得源来在实体空间中头、尾实体相似的实体在关系
r
r
r空间中被区分开。
- 对于每个关系
r
r
r,TransR设置一个投影矩阵
M
r
∈
R
k
×
d
M_r \in R^{k \times d}
Mr∈Rk×d,将实体
h
,
t
∈
R
d
h,t \in R^d
h,t∈Rd从实体空间投影到关系空间
r
∈
R
k
r \in R^k
r∈Rk空间,利用投影矩阵,实体的投影向量定义如下:
h ⊥ = M r h , t ⊥ = M r t h_{⊥} = M_rh,t_{⊥} = M_rt h⊥=Mrh,t⊥=Mrt

- TransH,沿法线进行投影
- TransR沿着投影矩阵进行投影。
经验
- 只有掌握深刻的数学知识,才能明白其中的含义,写出优秀的论文,慢慢自己学会积累都行啦的样子与打算。