Lecture 04: Pruning and Sparsity (Part II)

（笔记一）

Title	Pruning and Sparsity (Part II)
Lecturer	Song Han
Date	09/20/2022
Note Author	Saaketh Vedantam (saakethv)
Description	Discussing how to select the pruning ratio and how to fine-tune, introducing the Lottery Ticket Hypothesis, and describing system support for sparsity.

剪枝率

问：我们应该如何找到每层修剪比率？

• 浅层发现低层特征
• 更深的层发现抽象特征

问：哪些层的冗余度最高？

• 非均匀修剪比均匀缩放性能更好
• 更深的层具有更多的冗余（更多的通道，更多的重用功能），因此可以更积极地对其进行修剪

分析每层的敏感度

• 敏感度：修剪该层时精度下降多少

• 敏感度越高的层应减少修剪，敏感度越低表示冗余

敏感度分析：

• 挑选模型的 $L_i$ 层

  • 用不同的裁剪率裁剪 $L_i$ ，例如 r ∈ { 0.1 , 0.2 , … , 0.9 } r\in \{0.1,0.2,\dots,0.9\} r∈{0.1,0.2,…,0.9}
  • 观察每个比率 $r$ 下的精度下降， $\Delta {\text{Acc}}_i^r$

• 在所有的层上重复上述步骤

• 选择降级阈值 $T$，以使修剪比率达到所需的精度

优势：

• 很容易看到哪一层对修剪最不敏感，可以看到最后哪个的精度最高。
• 寻找压缩率的简单算法

劣势：

• 忽略层之间的交互-如果同时修剪两个层，精度会如何降低？
• 忽略层的大小-稍微修剪大层比大量修剪小层要好

自动剪枝

给定总体压缩比，我们如何选择每层修剪比率？

• 传统上需要大量的人力监督-我们如何实现自动化？

AMC (AutoML for Model Compression) [He et al., ECCV 2018]

• 将修剪视为强化学习问题

  • Reward: -错误率-大尺寸的惩罚

    • 受限于 #FLOPS 或延迟

  • Action: 按某种稀疏比压缩层（$[0,1)$ 中的连续数）

  • Embedding: 神经网络结构（通道数、内核大小等）

  • 使用 DDPG 代理完成学习

• AutoML 可以比人类更有效地进行修剪

• 自动学习删除冗余卷积的良好策略

NetAdapt [Yang et al., ECCV 2018]: 基于规则的迭代剪枝方法

• 查找每层修剪比率以满足全局资源约束

• 例如，延迟约束

  • 在每次迭代中，将延迟减少 $\Delta R$

  • 使用预先构建的查找表进行层修剪/延迟度量

  • 对于每层

    • 根据查找表将该层修剪 $\Delta R$
    • 微调一点，测量精度

  • 以最高精度修剪该层

• 重复此操作，直到总延迟减少满足约束

• 返回一系列延迟不断减少的模型

微调和训练稀疏网络

目标：在修剪模型后恢复网络的准确性。

• 学习率应为原始学习率的1%-10%，因为模型已经训练过

Iterative Pruning [Han et al., NeurIPS 2015]

• 一次迭代中修剪然后微调
• 根据需要重复多次
• 可能比一次修剪效果更好，因为模型会随着稀疏度的增加而逐渐学习

正则化技术：

• L1: $L^{\prime }=L(x;W)+\lambda |W|$
• L2: $L^{\prime }=L(x;W)+\lambda ||W|{|}^2$
• 适合修剪，因为它惩罚非零权重并鼓励较小的参数

彩票假说

问题：我们可以从头开始训练稀疏的神经网络吗？

• LTH: Yes!
• 目前，我们训练一个完整的模型，并在
• 从一开始训练的修剪网络实现了较低的精度

Lottery Ticket Hypothesis [Frankle et al., ICLR 2019]: 一个随机初始化的密集 NN 包含一个子网络，该子网络可以在训练最多与原始网络相同的迭代次数后，进行训练以匹配原始网络的测试精度。

• 想法：迭代幅度修剪
  • 训练完整模型，然后按大小进行修剪
  • 将修剪后的网络的权重重置为初始初始化-给出“中奖票”
  • 问题：仍然需要训练完整模型
• 相反，将权重重置为少量迭代后的权重 [Frankle et al., arXiv 2019]
  • 可以通过实验找到 #iterations (k)

稀疏度的系统支持

因为神经网络是非凸的，所以我们过度参数化它们，以便训练它们收敛

• 不利于推理，尤其是在内存受限的情况下
• 因此，我们需要模型压缩以实现更快和更高效的推理

EIE (Efficient Inference Engine) [Han et al., ISCA 2016]: 稀疏 DNN 模型的第一个加速器

• 每当乘数为 0 时，通过将输出设置为 0 跳过零步乘法
  • Weights: 静态 稀疏性
  • Activations 动态 稀疏性
• Quantization: 近似权重为 4 位，而不是 32 位
• 与专用处理元素（PE）和额外元数据（非零元素索引）并行

与传统压缩技术相比，EIE 实现了显著的加速和能效

• 现在，它在 NVIDIA GPU 中实现了商业化

不均衡负载

问题：我们可以共同设计剪枝算法和高效推理吗？

• 负载不平衡：由于矩阵的每个部分中的非零项不平衡，某些 PE 可能比其他 PE 有更多的工作
• *平衡 *修剪意味着在 PE 之间更均匀地分布稀疏度 [Han et al., FPGA 2017]
  • 不会降低精度
  • 比负载不平衡网络更快

M:N 稀疏度

• 在每组 N 个元素中，至少 M 必须为0

• 常见用例：2:4 稀疏度 [Mishra et al., arXiv 2021]

  • 将所有非零元素向左推，将矩阵压缩一半
  • 为每个元素存储 2 位索引

• M:N 稀疏度在 NVIDIA 张量核上实现矩阵乘法

（笔记二）

Title	Pruning and Sparsity (Part II)
Lecturer	Song Han
Date	09/20/2022
Note Author	Alex Gu (gua)
Description	Introduce and motivate pruning; outline the pruning process and granularities; overview pruning criteria

本讲座提纲

• 解释修剪，介绍如何选择修剪比例和如何微调
• 介绍彩票假说
• 介绍系统如何支持修剪神经网络中的稀疏性

章节 1：剪枝率

本节的目标是了解如何查找每层修剪比率。回想上一次的经验，非均匀修剪比均匀收缩效果更好。

然而，我们应该如何找到每一层的修剪比率？

分析每层的敏感度

第一种方法背后的想法是，不同的层对修剪的敏感性不同。在高级别上，我们分析每个单独层的敏感度（保持其他层不变），然后根据敏感度按比例修剪每个层。更具体地说：

• 首先，对于每个层 $L_i$，用不同的修剪比率修剪该层，并观察每个修剪比率的精度降低 $\Delta Ac{c}_r^i$。
• 可以使用不同的修剪率，比如 r ∈ { 0 , 0.1 , ⋯   , 0.9 } r \in \{0, 0.1, \cdots, 0.9\} r∈{0,0.1,⋯,0.9}.
• 然后，选择降级阈值 $T$。对于每一层，尽可能地进行修剪，而精度不会低于 $T$。

这种方法不是最优的，因为它独立地处理层，并且不考虑它们的交互，但是这种方法非常健壮，并且易于在实践中实现。

AMC: AutoML for Model Compression [He et al., 2018]

我们看到，以前的方法有一个主要的警告，即不能考虑不同层之间的交互。下一种方法 AMC（AutoML for Model Compression）将修剪视为强化学习问题。

State: 该状态使用 11 个特征表示，包括层索引、通道数、内核大小和 FLOP。

Actions: 我们使用 $a\in [0,1)$ 中的连续动作空间来指示该层的修剪比率。

Agent: 我们使用 DDPG（off-policy，actor-critic）代理，如下所示：在每个时间步，代理接收表示环境层 $t$ 的状态 $s_t$。代理输出动作 $a_t\in [0，1）$，并使用某种算法（如信道修剪）将层压缩为稀疏比 $a_t$。然后，代理移动到具有新状态 $s_{t+1}$ 的层 $t+1$。在最后一层之后，在验证集上评估模型，代理收到奖励。

Reward: 一个可能的奖励是 $R_{err}=-Error$，这鼓励模型减少验证损失。然而，这并不能激励模型尺寸的减小。因此，实现这种减少的一种方法是限制动作空间：允许前几层的任意动作，然后约束后几层的 $a_t$。其他可能的奖励包括 $R_{\text{FLOPs}}=-Error\cdot \log (\text{FLOPs})$ 或 $R_{\text{Param}}=-Error\cdot \log (\text{Number of Params})$.

作者表明，AMC可以将生成的模型修剪到比人类专家更低的密度，精度损失可以忽略不计。

有趣的是，该代理还了解到 $3\times 3$ 卷积层可以被修剪多于 $1\times 1$ 卷积层。

最后，与 MobileNet 相比，AMC 能够实现 2 倍的加速，而不会降低精度。

NetAdapt: A rule-based iterative/progressive method [Yang et al., 2018]

另一种方法，NetAdapt，找到每层修剪比率，以满足全局资源约束，如延迟或能耗。在高层次上，在每次迭代中，NetAdapt 都会生成许多网络提案，并根据预算对其进行评估。然后使用这些度量在下一次迭代中提出建议，依此类推。

作为一个说明性示例，考虑将延迟减少一定量 $\Delta R$ 的约束。作为网络方案，我们查看每一层，并使用查找表来修剪该层，以便延迟减少至少 $\Delta R$（方案模型A、…、Z）。然后，我们对模型进行短期微调（10k 次迭代），并在微调后测量精度。然后，我们以最高精度（C）修剪图层。然后我们重复，直到延迟减少满足约束。最后，我们对模型进行长期微调，以恢复原始精度。

由于迭代的性质，我们得到了一系列具有不同资源约束的模型，每个算法迭代一个。

章节 2：微调/训练

迭代裁剪

修剪后，模型的性能可能会降低。缓解这种情况的一种方法是微调修剪后的神经网络，允许更高的修剪比率。作为启发式，当微调时，使用原始学习率的 1/10 到 1/100 的学习率。我们可以反复修剪和微调以获得更好的性能 [Han et al., 2015]

正则化

当训练神经网络或微调量化神经网络时，加入正则化以惩罚非零参数并鼓励较小的参数。最常见的正则化器是 L1, $L^{\prime }=L(\mathbf{x};\mathbf{W})+\lambda |\mathbf{W}{|}_1$) 和 L2, $L^{\prime }=L(\mathbf{x};\mathbf{W})+\lambda \Vert \mathbf{W}{\Vert }^2$.

一些例子是，基于大小的细粒度修剪在权重上使用 L2 正则化，而网络瘦身 Liu et al., 2017 对信道缩放因子应用平滑 L1 正则化。

ADMM

讲座中未涉及的网络修剪的最终方法来自 [Zhang et al., 2018] ，并将经典优化技术应用于模型修剪问题。我们可以将修剪写成
$$\arg \underset{{\mathbf{W}}_P}{\min }L(\mathbf{x};{\mathbf{W}}_P)+g({\mathbf{W}}_P),g({\mathbf{W}}_p)=\{\begin{array}{ll}0& \Vert {\mathbf{W}}_P{\Vert }_0\le N\\ \infty & otherwise\end{array}.$$
这可以被写成：
$$\arg \underset{{\mathbf{W}}_P}{\min }L(\mathbf{x};{\mathbf{W}}_P)+g(\mathbf{Z})\text{s.t.}{\mathbf{W}}_{\mathbf{P}}=\mathbf{Z}.$$
其想法是写出增广拉格朗日量并应用 ADMM。我们推荐感兴趣的读者阅读这篇论文。

章节 3：彩票假说 [Frankle et al., 2019]

彩票假设如下：一个随机初始化的密集神经网络包含一个子网络，该子网络被初始化，使得当单独训练时，在训练最多相同次数的迭代后，它可以匹配原始网络的测试精度。

这是什么意思？早些时候，我们看到我们可以训练一个神经网络，对其进行修剪，然后对修剪后的网络进行微调。如果我们没有对修剪后的网络进行微调，而是从头开始训练它呢？当代经验表明，与原始网络相比，通过修剪发现的架构更难训练，精度更低。

事实上，大多数随机采样的稀疏网络都无法恢复原始精度。然而，仔细选择的子网络（称为中奖彩票）可以。

怎样通过迭代幅度修剪方法。假设你希望修剪 $p\%$ 个参数，并将修剪 $n$ 个迭代。首先，随机初始化神经网络 $f(\text{x};{\text{W}}_0)$。然后，训练网络进行一些迭代 $t$，以获取参数 ${\text{W}}_0$。我们删除 $p^{1/n}\%$ 参数，创建掩码 $m$。然后，设置 ${\mathbf{W}}_0\leftarrow m\odot {\text{W}}_0$，然后重复。请注意，在每个步骤中，权重都被重置为其原始值，所改变的是存在的连接集。

后来，作者们发现，将权重重置为 ${\text{W}}_0$ 仅适用于 MNIST 和 CIFAR 等小型任务，在较深的网络上失败 Frankle, et al. 2019。 相反，他们在少量训练迭代后将权重重置为值（在本例中，$t=6$）。

章节 4：稀疏性的系统支持

EIE: Efficient Inference Engine [Han et al., 2016]

EIE 是第一个用于稀疏压缩模型的 DNN 加速器。

EIE 利用了稀疏权重（计算量减少 10 倍，内存减少 5 倍）、稀疏激活（计算量降低 3 倍）和 4 位权重的权重共享（内存减少 8 倍）。

与 CPU 和 GPU 相比，EIE 实现了更好的加速、FLOP 减少、吞吐量和能效。

Accelerating Recurrent Neural Networks [Han et al., 2017]

首先，一个观察结果是 PE 是不平衡的：一些 PE 的非零权重比其他 PE 的多。因此，一个技巧是应用负载平衡，以便在 PE 中分布非零权重。这在不牺牲任何精度的情况下实现了更好的加速。

硬件体系结构由存储器单元、稀疏矩阵乘法单元和按元素单元组成。与 CPU 和 GPU 相比，我们在延迟、功耗、加速和能效方面看到了显著的提高。此外，发动机很容易适应不同的硬件。

M:N Sparsity [Mishra et al., 2021]

M:N 稀疏性意味着在每 $N$ 个连续权重中，最多 $M$ 是非零的。常见的情况是 2:4 稀疏，如下所示。我们不需要存储每个值，只需要存储非零数据值，以及表示 4 个连续块中哪 2 个元素是非零的 2 位索引。

系统对这种稀疏性的支持也相对简单，如下所示。注意，只需要进行一半的乘法运算。

基准测试表明，大型 GEMM 操作可实现 2 倍的速度提升，而不会降低精度。

---

Lecture 04 — Pruning and Sparsity (Part II)

今天我们将继续讨论剪枝和稀疏性，今天的第一个主题是我们如何为每一层选择合适的稀疏率，然后是如何微调以恢复准确率，提高学习率，是一次性修剪还是迭代进行，然后再介绍彩票假说，它表明有时可以从头开始训练稀疏神经网络。最后介绍修剪后对神经网络稀疏性的系统支持，并阐述了如何在通用和专用硬件上将计算缩减转化为测量的加速，我们将在本讲座的后半部分讨论这一点。

现在我们切换到确定剪枝率的新章节。

那么如何计算每一层的稀疏度是多少以及我们如何选择裁剪率？

在给定深度神经网络的情况下，让我们集思广益，考虑到深度神经网络，较浅的层与低级特征交互，寻找边缘、角落等特征，而较深的层正在寻找更抽象的信息，所以你认为哪一层具有更多冗余？较浅的层还是更深的层？

我们可以想出不同的启发式方法，这需要大量的手动调整，均匀剪枝是指每层使用相同的裁剪率，而通道剪枝，一些层裁剪的多、一些层裁剪的少，例如可能认为更深的层通常包含更多的冗余，尤其是如果网络中有很多 FC 层，这些 FC 层就可以更积极地进行裁剪，而较浅的层，尤其是第一层通常不容易被剪。

右边的图给出延迟和精度的理想关系图，我们想要更低的延迟、更高的精度，巧妙地选择每层的修剪率比仅统一缩放每个层可能更重要，例如这两个模型在手机 CPU 上都有大约 70 毫秒的延迟时，精度能差 2 个点。

所以为每一层选择适当修剪率很重要，然后问题是我们如何找到每一层的裁剪率？

如果我们通过反复尝试来证明，假设你的网络有 50 层，每层都有如 10%、20% 或者 50% 之类的选择，有点像 $n^2$ ，这是一个巨大的选择，所以我们可以做一些启发式，分析每一层的敏感性，你修剪它一点点，看看准确率是如何下降的？你会继续证明更多一点，看看准确率是如何下降，然后再做更积极的修剪。

如果该层不那么敏感，基本上你可以修剪很多而不会失去准确性；但如果它非常敏感，你修剪一点点，性能就会急剧下降，让我们一层一层地运行它，看看它是如何发生的。（这需要重复训练多少遍 😦）

大家可以在我们的入门代码中进行设置，让我们从原始的原始神经网络开始，一开始准确度非常好，大约 93 的精度， 对于第一层我们逐渐修剪 30%、40%、50%、60%，然后精度开始下降得非常快。

第二层（绿色）裁剪 70% 还可以保持很好的精度，直到 90 左右才下降了一点点，这意味着该层可以多剪一些。

这个方法的局限性是什么？到目前为止，我忽略了什么？层之间的相关性，是的，这是其中之一。

我们如何选择修剪比率？我们只给出一个阈值，说我们希望损失不超过 5% 或 10% 等，然后通过图中交叉点确定每层的裁剪率，例如蓝色的层比较敏感，大概在 72% 左右就可以，而不太敏感的层可以超过 80%。

这是最优的方式吗？当然不是，因为我们正在独立考虑每一层，所以这是你想做多少实验与理想值的近似之间的权衡，即使在设计某些 AI 工具时，这也是一种非常广泛使用的启发式方法，因此，如果你想设计芯片，你想做一些加速裁剪，请随意使用这种方法，它非常健壮，很容易做到。

我们可以超越这些启发式方法吗？是否有更多的自动化方法来考虑神经网络的整体性？

另一个限制是，如果你的目标是整体能有更好的修剪比率，那么这里缺少的是什么？到目前为止，我们是从敏感度-准确度的角度分析的，我们希望我们不会对这些敏感层失去太多的准确度。所以还应该考虑哪些因素，使我们能更准确地确定每层的裁剪率。

例如这个绿色层甚至非常不敏感，如果对它只进行少量参数修剪，这对我们没有太大帮助，但我们也不要过于积极地修剪它，而对于像红色的层，虽然它非常敏感，比如说它贡献了 90% 的参数，但我们只是稍微正确地修剪它，可能也会有很大帮助，所以这是我们要考虑的另一个因素，因为决策的复杂性，能有一个自动化的方法是非常重要的，它是否有可能提高准确率，例如当你裁剪的太多，十个类别中有九个是好的，但其中一个完全被破坏了，那它也不再是好的模型了。所以设计一个合适的奖励是非常重要的，准确率是一个很好的指标，但可能还要考虑很多，比如计算量、激活大小、模型大小、推理延迟等。

那么接下来，这促使我们进行复杂的空间设计，以进行更为自动化的修剪方法，因此，在给定总体压缩比的情况下，我们如何选择每层的裁剪率。

敏感度分析忽略了层之间的交叉相互作用；传统上这种修剪需要机器学习专家和硬件专家的经验知识。

我们希望让这位非专家有一键式的解决方案，能够弥补这种高效的神经网络设计与 AutoML 方法之间的差距，我们提出这种 AutoML 用于模型压缩，而不是让人类决定哪一层应该裁剪多少。

我们希望有一个代理来自动计算出每一层的裁剪率，这里我们使用强化学习代理来完成这项工作，这里我们有几个组件，我们有一个评判员（critic），我们有动作（Action），我们有嵌入（embedding）

critic 的作用是评判，好策略还是坏策略，所以我们需要清楚地定义奖励函数，最简单的奖励函数是错误率，我们想要低错误率，但这还不够，我们还想惩罚长延迟、惩罚一个大的模型大小，这样你就可以在奖励函数中添加不同的项。

什么是动作，这里的动作是每一层的稀疏率，例如第一层 30，第二层 50 等。

我们还需要知道神经网络的嵌入，因为神经网络的架构决定了正确的裁剪策略，我们想对这些嵌入进行编码 ，有 NCHW 和每层的索引，我们想把它们放入特征中，这样代理就可以使用这个特征来给出动作。

参考资料：

论文：AMC: AutoML for Model Compression and Acceleration on Mobile Devices

翻译：https://blog.csdn.net/weixin_50862344/article/details/128882540

官方 github：https://github.com/mit-han-lab/amc

Intel 的蒸馏工具包：https://github.com/NervanaSystems/distiller

它使用强化学习代理的以下设置，当我们设计状态时，有 11 个特征，包括层索引，通道数，内核大小、FLOPs 等；动作基本上是每一层的已验证比率，它是一个连续的数字，这就是我们使用 DDPG 代理的原因，代理本身超出了本课程的内容，如果你正在参加强化学习课程，你将了解此代理，因此它支持连续动作，而不是像离散的”上下左右“，稀疏比在 0 和 1 之间。奖励是负的错误率，错误率越低奖励越大。我们还可以使用预先构建的查找表（LUT）优化延迟约束。

这是比较人类修剪的和自动修剪的模型比较，这是 imagenet 上的 ResNet 50，这个实际上来自我的博士论文，我花了将近一周的时间来弄清楚我们应该为每一层修剪多少，从不同的手动调整，调整大约一周我找到不同层的修剪比率，我得到 29%，它非常好，小三倍。但是我们使用这个 AMC 代理，在短短几个 GPU 小时内我们就可以将它修剪到只有 20，比人工调整的还好。

右图的密度是指非零的参数量/总的参数量，对于不同的阶段（迭代剪枝的阶段）用不同的颜色着色，代理自动发现 3x3 有较多的冗余，可以裁剪的更多，而 1x1 卷积的冗余度低，裁剪的少，我们从来没有通过反复试验教给代理这样的规则，这非常有趣。

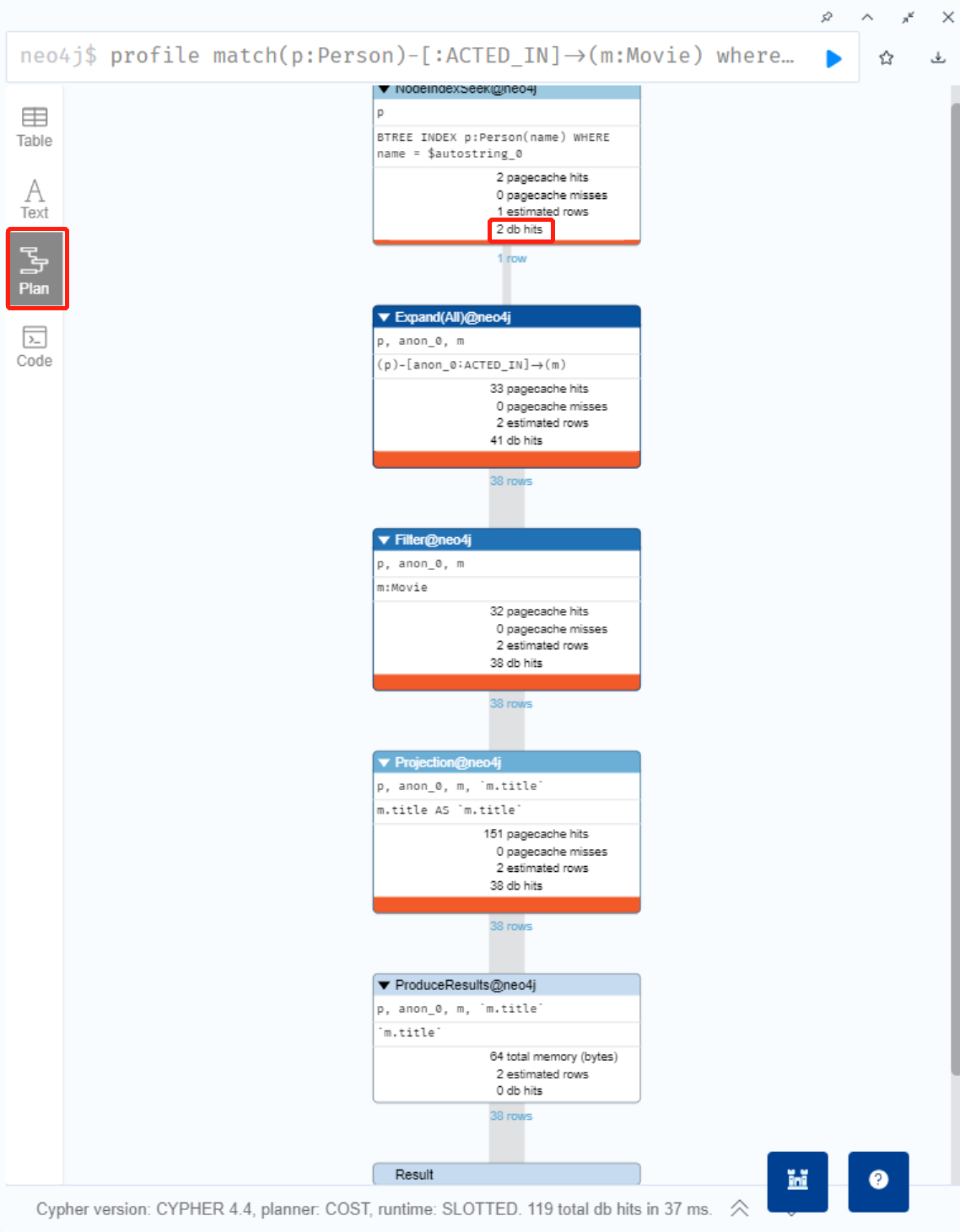
这里显示了 MobileNet 网络的剪枝效果，原始模型 569M，延迟是 119ms，将计算量减少一半，精度几乎不变，加速 1.8 倍；如果将延迟压缩一半，精度下降的也不是很明显。

而如果我们天真地将所有层线性缩放 0.75，我们会得到更差的精度和更长的延迟，这表明这种自动化方法更好，不仅仅是纯粹线性缩放，而是所有层。

这里介绍另一种方法来自动找到我们应该为每一层裁剪多少，称为网络适应（NetAdapt），目标是相似的，也是找到每层最佳剪枝比率以满足全局约束。

给定一个四层神经网络，对于每一次迭代，我们的目标是将延迟减少 $\Delta R$，我们尝试不同的层，例如，对于第一层，我们要删减多少，以便我们能够满足 $\Delta R$ 的延迟减少，然后我们通过短期微调来记录这种情况下的准确度，以了解准确度的损失，然后我们尝试第二层稍微删减，直到我们完成了所有层的准确性工作。

这种方法可以产生一个 model 系列，而且也始终优于其他的一些方法，如直接将模型乘以 0.75 或 0.25

参考资料：

paper：https://arxiv.org/abs/1804.03230

code：https://github.com/madoibito80/NetAdapt

tutorial：https://blog.csdn.net/qq_38156104/article/details/107716539

它将优化之后的网络部署到设备上直接获取实际性能指标，之后再根据这个实际得到的性能指标指导新的网络压缩策略，从而以这样迭代的方式进行网络压缩，得到最后的结果。

算法步骤：

1. 选择当前层需要剪掉的 filter 数量
2. 确定哪些不重要的 filter 需要被剪裁掉。
3. short-term 的 finetune 使其恢复精度，选择其满足资源需求且 finetune 之后网络性能最好的
4. 判断当前迭代论述的模型是否满足算法预先设计的资源需求限制，若满足则对模型进行 long-term 的finetune 得到最后的结果；

我们现在学习有关如何指定稀疏率的三种方法：

1. 通过这种敏感性分析，它非常简单、非常快速，但没有捕捉到层之间的交互
2. 第二种方法是 AMC 方法，使用强化学习代理找出最好的个体，
3. 第三种 NetAdapt，使用这个每层 $\Delta R$ 分析来查看哪一层的准确性下降最少

接下来，我们了解如何微调和训练稀疏改进神经网络以及我们如何在修剪后恢复准确性。

当我们微调模型时一个非常关键的点是我们需要降低学习率，因为我们的模型已经训练有素并且几乎收敛了，微调的学习率大概是原始学习率的 1% 或 10% 左右。右图显示了微调前后对比效果，裁剪 80% 后经过微调完全恢复原始准确率。

一个好的做法是不要将模型直接修剪到你想要的目标稀疏度，假设我的目标稀疏度是 90%，你想一步一步地，修剪一点，微调一点，然后再裁剪微调它，这是一个很好的做法，这样我们就可以到达这条红色曲线。

并且在微调期间我们想要添加正则化以鼓励权重，在调整模型时我们想要鼓励权重更接近于零，以便更容易正确地修剪它们。主要有 L1 和 L2 正则化方法，在我们的实践中，我们使用这些正则化更多一点，但实际上它们在两种情况下的效果都差不多。

到目前为止，有关剪枝的内容，我们基本都涵盖到，右图是对网络剪枝的问题定义，前文已提到过。

（有关 ADMM 方面的内容，在视频讲座中未提及）

paper：A Systematic DNN Weight Pruning Framework using Alternating Direction Method of Multipliers

本文是将 weight pruning 看做一个有稀疏率等组合约束的非凸优化问题，这样的话则可以将原非凸优化问题分解为两个子问题（即模型收敛以及模型稀疏率约束两个子问题）来进行迭代求解（即使用交替方向乘子法-ADMM迭代求解）。其中模型收敛问题可以用随机梯度下降法解决，另一个稀疏率等约束问题可以用解析法解决。相比之通常用的启发式剪枝方法收敛速度上会更快一些。

blog：https://zhuanlan.zhihu.com/p/270413414

让我们谈谈最近的一些关于彩票假说的文献，我们可以直接从头开始训练这个稀疏神经网络吗？一些经验表明，这样的模型从头很难训练，且精度低。

两个模型在 MNIST 和 CIFAR10 上的比较，虚线基本上是随机采样的稀疏神经网络，你有一个密集的网络，你随机采样稀疏的一个子集，神经网络改进得越多，实际上准确度越低。

但有一条实线表示是在保持准确性的同时，即使修剪率非常高，那条线是什么，它应用了正确的稀疏掩码，我们稍后会讨论，它使用相同的初始化。

最初你初始化模型，然后你一直训练到最后，当它收敛时，你会发现哪一个权重很大，你保持这些权重，这样你就知道稀疏性模式，那些重要的权重是获胜的票，它们的质量为 1，然后你在开始训练网络时使用相同的掩码，你使用相同的初始化，你训练到最后，你可以获得这条线，即使只剩下 1.2% 的权重，也可以获得相当好的准确性。

总结起来，彩票假说是说，一个随机初始化的密集神经网络包含一个子网络，该子网络被初始化，使得当单独训练时，它可以在训练最多相同次数的迭代之后匹配原始网络的测试精度。

这有一个例子，随机初始化的模型用浅蓝色表示，我们正在训练 T 个 epochs，然后权重变为深蓝色，获胜的彩票基本上是说我们发现我们在模型中保留了这些大的权重，然后重新用初始的浅蓝色来初始化这些权重，但应用这个 mask，在最多 T 个 epochs 内修剪这个模型，你可以获得与之前相同的精度。

观察第三个和第四个模型，它们有相同的稀疏模式，但它们有不同的权重，前者已经训练收敛，后者是最初的初始化权重，然后我们训练它，然后我们对它进行更多的修剪，所以注意到第六个模型的稀疏性比前者更大，有些边又被裁剪掉了。

然后重复上面的过程，我们在收敛到最后这个模型后，再次使用它的稀疏掩码，但是还是最初模型的初始化权重，再次构建新的子网络（左下角），然后我们可以训练它，最终我们可以获得相同的精度，尽管这个模型比一开始的模型小得多，但具有相同的精度。

所以棘手的部分是我们仍然必须训练模型，当它收敛以获得这个稀疏掩码。

在将权重重置为非常初始的初始值的情况下，存在缩放限制，这适用于像 MNIST 和 CIFAR-10 这样的小规模任务，但图像网络上的更深的网络实际上不起作用，相反，不将权重重置为 $W_{t=0}$，而是初始化在少量 $K$ 次训练迭代之后的 $W_{t=k}$，可以稳健地获得修剪的子网络，我们需要手动探索。

这样我们仍然可以恢复像 imagenet 这样的大规模数据集的准确性，我们可以更好地恢复精度，训练 epochs 总数为 90，我们回退到第 6 轮的参数。

具体的回退，它真的依赖于数据集。

让我们继续讨论，算法硬件代码设计以及对稀疏性的系统支持，（接下来几页内容均为回顾，略）

因此，传统的范式是，你在模型中是正确的，然后你获得模型，如果你使用直接部署模型进行推理，那么这样做的缺点是什么？

因此，我们正在使用 SGD 优化算法来处理这样一个高度非通用的模型，神经网络实际上需要大量冗余和过度参数化，以确保我们能够获得良好的收敛性，但实际上该模型是过度参数化的，推理效率非常低，直接部署它会消耗大量不必要的和计算，这在移动设备上可能会非常慢。

所以更好的范式是在训练之后，不直接部署，而是先压缩，删除那些冗余的参数，得到一个轻量的模型，然后用专门的硬件运行加速，速度快而且更省电。

这里我们有三个非常基本的规则：

• 任何乘以零的东西都是零，任何权重为 0 的东西，不必去计算它
• 如果 ReLU 激活为零，也不需要乘它
• 对于深度神经网络，我们不需要 2.09、1.92 的高精度，近似为 2 就可以（量化）

对于 90% 权重为 0 的情况下，计算量可以减小 10 倍，内存占用也会减少 5 倍（主要是还要存储索引或 bit Mass 等）；而对于激活，我们通过 ReLU 通常可以得到 70% 的 0，但这是动态的，稀疏性是在运行时确定的，所以无法减少内存占用，但可以降低计算量，如果你更聪明的话，也许未来也可以，因为你可以使用更聪明的数据结构来表示这些激活；量化可以减少内存占用，例如从 32-位减低到 4-位，可以减少 8 倍的存储，但是计算量不变。

在剪枝之后，权重矩阵开始变得超级稀疏，例如，我们有 一个大小为 4 的向量，矩阵是 8x4，你可以看到很多权重实际上被修剪为零，输出维度在这种情况下是 (8x1) = (8x4) x (4x1)

因此，我们想分析如何并行化以及如何跳过这些零，高效推理引擎(EIE)是第一个可以利用权重稀疏性，具有通过对神经网络进行修剪能力的加速器。

因此，我们首先将其映射到不同的处理元件，每种颜色表示不同的处理元件，在本例中，我们有四个处理元件，首先，PE0 处理负责第一行和第五行，PE1 负责处理第二行和第六行，以此类推。

物理上，它们是这样存储的，所以对于矩阵来说，例如给定绿色 PE0，我们想只存储这些非零元素，在这种情况下有 ，$w_{0,0},w_{0,1},w_{4,2},w_{0,3},w_{4,3}$，我们还要存储这些相对索引，

这种存储方法是 compressed sparse column(CSC) 的变体，我们先介绍 CSC 格式，与 CSC 对应的是 CSR 也就是按行压缩的格式。

>>> from scipy.sparse import csr_matrix
>>> import numpy as np

>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 1, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> A = csr_matrix((data, indices, indptr), shape=(3, 3))
>>> A.toarray()
array([[1, 2, 0],
    [0, 0, 3],
    [4, 5, 6]])

data 中存储的就是矩阵中的非 0 数据，按行遍历的；indptr 中包含 4 个元素，这 4 个元素可以确定 3 个区间，0-2, 2-3, 3-6。以 0-2 为例：indices[0:2] -> [0, 1]，这说明，在第 0 行中 0, 1 两列有值，分别是data[0:2] -> [1, 2]，这样整个第 0 行的数据就是 1 2 0；同理，2-3 这个区间 indices[2:3] -> 2，也就是只有第 2 列有值 data[2]->3，这样整个第 1 行的数据就是 0 0 3；

>>> from scipy.sparse import csc_matrix
>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> csc_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 4],
    [0, 0, 5],
    [2, 3, 6]])

CSC 只不过是按照列的顺序遍历 data 的，例如 0-2 这个区间 indeces[0:2] -> [0, 2]，说明第 0 列 的第 0、2行的值分别是 data[0:2] -> [1, 2]，也就是整体上第 0 列的数据是 1 0 2，以此类推。

我们再反过来看这个 CSC 变体格式，它首先将矩阵的每一列独立出来，分别用 $v$ 和 $z$ 表示非 0 元素列表和相对位置编码，这里的位置编码通过是 4 byte，也就是只能记录 0~15 的范围，如果超过 15 的范围，则要插入一个 0 元素，不进行压缩。这段话，需要结合下面的例子进行理解，例如矩阵某列元素如下：

$[0,0,1,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,O,0,0,3]$

$v$ 是非 0 元素的遍历，按理来说应该 $v=[1,2,3]$，$z=[2,0,18]$，分别表示数据 1 前面有 2 个 0，数据 2 前面有 0 个 0，数据 3 前面有 18 个零，但前文说到，我们最多只能记录 0~15 个 0，这样的话，第 16 个 0 的位置就需要保留（我用大写的 ”O“ 表示），这样 $v=[1,2,0,3]$，$z=[2,0,15,2]$

然后多个列的 $v,z$ 分别对应拼接，此时需要一个 $p$ 指针列表，记录各列的区间范围。

有了上面的基础，这张图就能看懂了，首先，PE0 代表绿色部分的数据，按列顺序遍历，分别得到 $w_{0,0},w_{0,1},w_{4,2},w_{0,3},w_{4,3}$，最开始是 $w_{0,0}$，前面没有 0，所以 Relative Index 的第一个数字是 0，然后是 $w_{0,1}$ 它前面有个 $w_{4,0}$ 位置是 0，所以前面有 1 个 0，Relative Index 的第 2 个数字是 1，依次类推，数各自前面 0 的个数。然后 Column Pointer 的作用类似前文介绍的 indptr 划定区间的作用，后一个数字减前一个数字，例如区间 0-1 代表第 0 列只有 1 个数据，最后一个区间 3-5，表示第 3 列有 2 个数据。

右图来自于论文中，关于 Relative Row Index 的记录方法是每个列独立从 0 计数，以 $w_{0,2}$ 为例，如果按照上面的方法，拼接前面的列，则 $w_{0,2}$ 前面有 2 个 0，分别是 $w_{8,1},w_{12,1}$，但论文中是每个列独立计数的，此处是 0。

现在你应该明白为什么当裁减了 90% 的权重，内存节省了不到 10x，因为除了非 0 元素本身，还要保存一些索引等元数据。

这是元素中每个进程的微架构，以加速这种响应和修剪模型，

我们有激活队列，我们可以看到不同的 PEs，它们可能有不同数量的非零元素，所以我们要确保它们是平衡的，并制作一些缓冲区。然后我们通过检查输出是否为零来巧妙地处理这个激活，如果这不是零，那么我们通过权重矩阵传递它，就像我们刚才提到的那样，我们有这个列的开始和结束地址，还有稀疏权重矩阵，所以我们发现这些非零元素，然后解码权重，所以我们将在下一节关于权重共享和权重解码的讲座中讨论。

然后，对于地址，记住我们存储这些相对索引，因此我们需要累加它们以获得绝对索引，然后我们进行乘法和加法，我们还并行存储地址，因此我们可以将其存储到相应的位置并更新输出激活 SRAM。

所以实际上，关键的计算是这个修改。我们必须做大量的实际工作来指导我们应该在哪里读，在哪里写，最后我们将其通过 ReLU 单元，并检测它是否是零，如果非零，我们也要将其放入下一阶段的激活队列中。

所以特别的部分是激活队列，我们要进行负载平衡，我们还有权重解码器，将 4 位量化索引转换为16位实际权重值，还有这个地址累加器，将相对索引转换为绝对索引。

左图是高效推理引擎的布局，右图是稀疏率。

你只能处理 FC 层，这是 AlexNet 的 FC 层，具有稀疏性和条件稀疏性，这是通过将权重密度与激活密度相乘来减少Flop，这是 vgg 模型的 FC 层，最后这是图像捕获模型，我们观察到，为什么这些模型的激活密度是数百，实际上他们没有使用 relu，这就是为什么我们没有这些图像捕捉模型的激活稀疏性，他们使用 sigmoid，这就是我们对这些模型的图缩减较少的原因。

并且与 CPU 和 GPU 相比，它的速度相当不错，（每组右侧的条柱）这些模型实际上是压缩的，所以即使在 CPU 上运行压缩模型，也可以比非压缩模型具有相当大的优势。

右图是对CPU、GPU、mGPU 的能效和高效推理引擎的比较。

我们可以发现，一般来说，运行压缩模型比运行非压缩模型有很大的优势，这是 2015 和 16 年的早期原型，但几年后的 2021，当 Nvidia A100 问世时，这项技术已经在 Nvidia-GPU 中稳固地商业化，支持 2:4 稀疏性。

（右图），在 EIE 之后，我们制作了一个 FPGA 原型，不仅可以加速这些 FC 层，还可以加速这些递归神经网络，这些神经网络广泛应用于语音识别、图像字幕、机器翻译和 VQA 中。

因此，来谈谈语音识别，之前我们进行压缩，然后在压缩模型的基础上进行加速推理，所以我们想重新思考设计流程，当我们设计加速器时，我们应该做什么？当我们进行剪枝时，我们可以做得更好吗？我们可以同步设计剪枝算法与推理引擎吗？

所以这里我们发现负载平衡是一个非常关键的问题，在这种情况下，这个绿色 PE 有 5 个非零条目，PE3 只有一个非零元素，所以周期的总数取决于具有最大元素数的 PE0。因此，当我们进行修剪时，应该使每个 PE 大致具有相似数量的非零元素，因此这是硬件对修剪算法的指导，这样整体循环非常平衡。

但这是我们必须添加的实际限制，它是否会损害准确度？我们进行了这项分析，红色线是没有负载平衡的，我们可以证明裁剪大约 90% 的参数，而不会显著增加 phone 错误率，但如果我们应用这种低的平衡，我们仍然可以实现类似的修剪比率，而不会增加错误率，所以通过使用这种负载平衡感知的修剪非常有用。

但是记住当我们没有负载平衡时，会有一些额外的工作需要等待，对于没有负载均衡的，我们的速度提高了 5.5倍，但如果我们采用负载均衡，可以在不影响精度的情况下，在密集模型上提高 6.2 倍的速度，因此这确实表明了该算法和硬件协同设计，其中硬件功能实际上指导了更好的软件修剪，修剪算法将导致更好的速度，而不会改变RTL，所以这是完全相同的监视器，完全相同的 RTL，但可以通过更多的属性删减模型模型架构以实现更好的速度。

右图是整个构建块内存单元稀疏对称矩阵乘法单元以及这些元素单元。

这是 Xilinx KU060 的 FPGA 上的原型，与 2016 年的 GPU 和 CPU 的延迟进行比较，所可以通过调用 Titan X，但现在我们的 GPU 都要好得多，功耗与速度和能效（如专用型号）相比通常具有更高的功耗，但实际上另一个因素对深度学习计算是一种可编程性，也是软件如何容易适应不同的模型架构。

这张幻灯片显示了这种专用加速器的优点和缺点，这是我在 2017 年设计的，实际上一年后，Transformer 模型问世，Bert 问世，深度学习社区正在快速发展，因此可编程性、适应能力和灵活性非常重要，因此当你处理 AI 推理引擎、AI 芯片和 AI 硬件-这种灵活性是一件最重要的事情，它是提高效率和速度的一部分，因此，这不仅对软件，而且对芯片设计者来说都是一个好建议，我们希望确保我们的模型是我们的硬件。与硬件结合得非常好，并且易于在软件堆栈上进行调整。

（以下 PPT 讲座中未公开，可以结合课件内容，选择性学习，因页数较多，不展示）

所以让我们快进到 2021，五年后，非常令人兴奋的是稀疏性、剪枝和模型压缩已经直接集成到 GPU 中，在 GPU 中，稀疏性得到了本地支持，使用的是一个改进版本，即 M:N 稀疏性，图中是 2:4 稀疏性，每四个元素中至少两个元素为零，你可以有三个零、四个零，但必须至少有两个零，另外需要两 bits 存储非零元素的索引。

我们如何聪明的加速它呢？在 Nvidia GPU 中可以支持这样的 2:4 稀疏度，右图中的左侧是稠密情况，右侧是稀疏情况，对于稠密矩阵，绿色是权重，红色是激活，一行一列你必须做 8 次乘法，然后把它们累加起来，得到这个黄色这个输出。

关于右侧这个权重矩阵的更新版本，我们不再恢复原始格式，而是采用稀疏格式，在这八个权重中，只有四个权重不为零，我们将它们放在这里，作为第一个操作数，根据索引矩阵，mask 掉激活矩阵中对应位置，使其具有相同的稀疏模式，因为零乘以任何东西都是零。现在只需要做 4 次乘法运算，理论上节省了一半的计算量。

所以这显示了 GEMM 的速度，这是在 K 维度上扫过的，我们可以观察到 K 越大，速度越快，大约在 2 倍的时候饱和，因为 2:4 最多可以节约一半；在左图右侧，显示了不同模型的准确度，主要是视觉模型，使用稀疏版本 vs 密集版本，准确度实际上维持的很好，这也是为什么采用 2:4，而不是 2:6 或 2:8 的一个原因，因为我们希望完全保持精度。

（以下内容，讲座中未提及，略）

所以总结一下今天的讲座，我们了解到了自动找到压缩比的方法，在敏感性分析中使用了非常实用的方法，我们讨论了这个有趣的部分，即彩票假设，这两个方向都是最终项目的好方向，继续探索干扰因素，我们还讨论了这个系统对压缩的支持，在下一节课中，我们将讨论量化效率规划中的另一个非常重要的概念，首先介绍那些数据类型以及自然合成的基本概念和常见的量化方法，这里是今天我们讨论的论文的参考资料，这就是今天讲座的全部内容，谢谢。