电子技术——分立CS和CE放大器的低频响应

我们之前在学习放大器中从来没有关系过信号频率对放大器的影响，也就是说我们默认放大器具有无限的带宽，这当然不符合现实逻辑。为了说明这一点，我们使用下图：

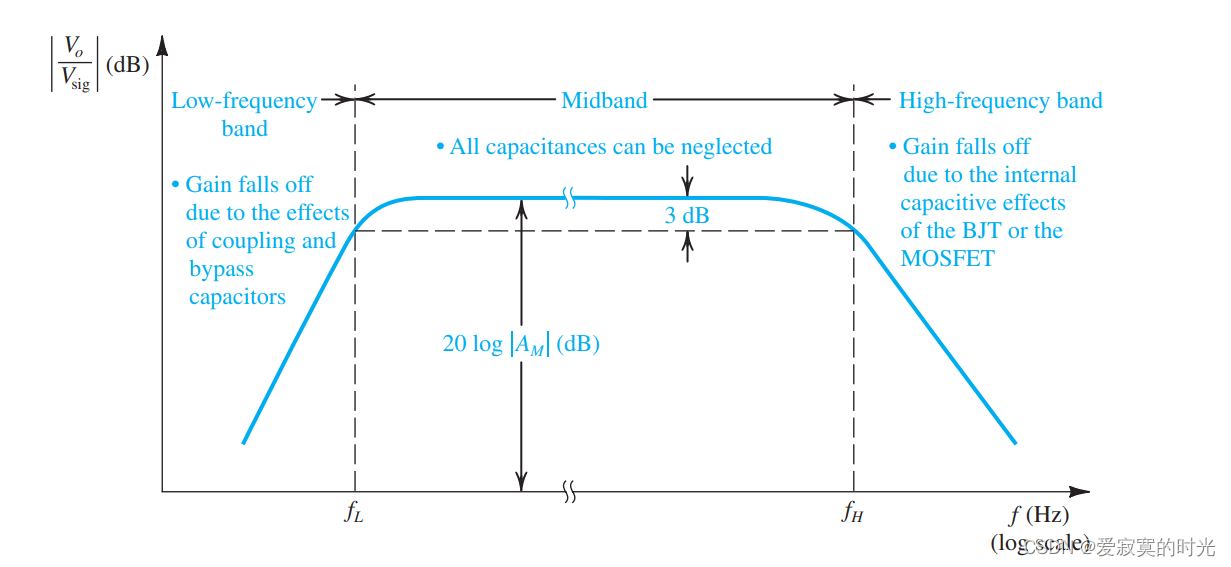
上图描述了MOS或BJT分立电路放大器的频率响应特性。我们发现存在中间一段区域，无论信号的频率怎么变化，放大器的增益都是一个常数。一般的放大器都工作在此区间，我们称这个区域为 中频带 。一个好的放大器设计应该让中频带处于我们想放大的信号频率上。如果不是这样，则放大器就会造成失真，因为不同频率的信号放大的倍数不同。

上图还展示了当信号频率较小的时候，放大器的增益就会下降。这是因为此时的耦合和旁路电容不在对信号具有低阻抗，回忆一下电容的阻抗为 $1/j\omega C$ 若信号频率越小，则阻抗越大。我们称 $f_L$ 为中频带的低频结束点，经常被定义为中频带增益的 $-3dB$ 下降点。我们本节将会讨论分立CS和CE放大器的低频响应。而对于集成电路来说，我们不使用耦合和旁路电容而是直接耦合，因此 $f_L=0$ ，如图：

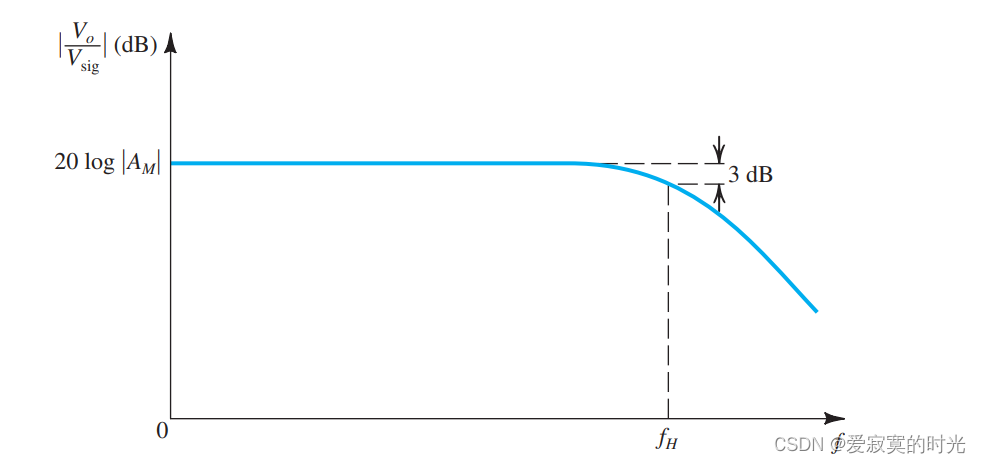
无论是分立电路放大器还是IC放大器都会存在一个中频带的高频结束点 $f_H$ ，经常被定义为中频带增益的 $-3dB$ 下降点，这是因为BJT和MOS的内部电容效应。我们将在后几个节学习如何在T模型或是混合 $\pi$ 模型中模型化内部电容效应。

则放大器的 带宽 定义为：

$$BW=f_H-f_L$$

一个对于放大器非常重要的特性是 增益-带宽积 定义为：

$$GB=|A_M|BW$$

增益-带宽积通常被用来权衡一个放大器的增益和带宽。

在本节我们探究分立CS和CE放大器的低频响应。

CS放大器

下图展示了一个典型的分立CS放大器的完整结构：

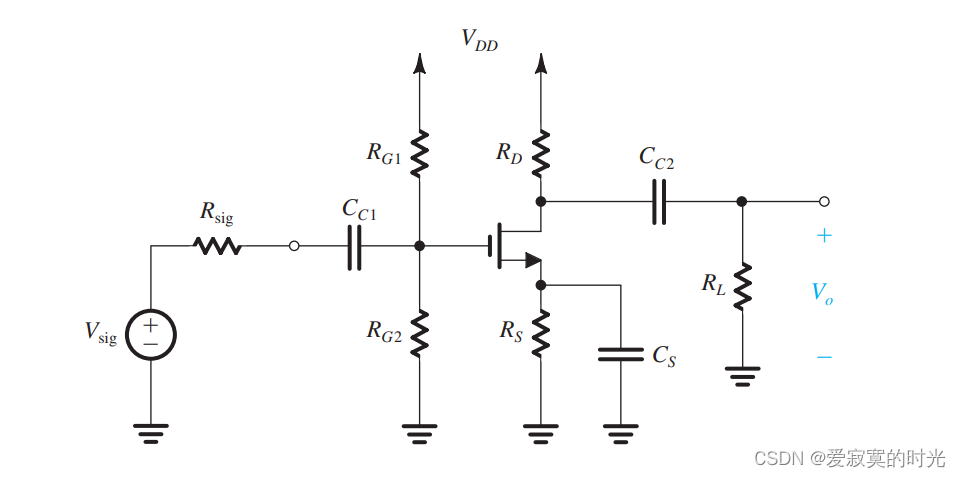
为了分析分立CS放大器在低频处的响应，我们使用下面的电路图进行研究：

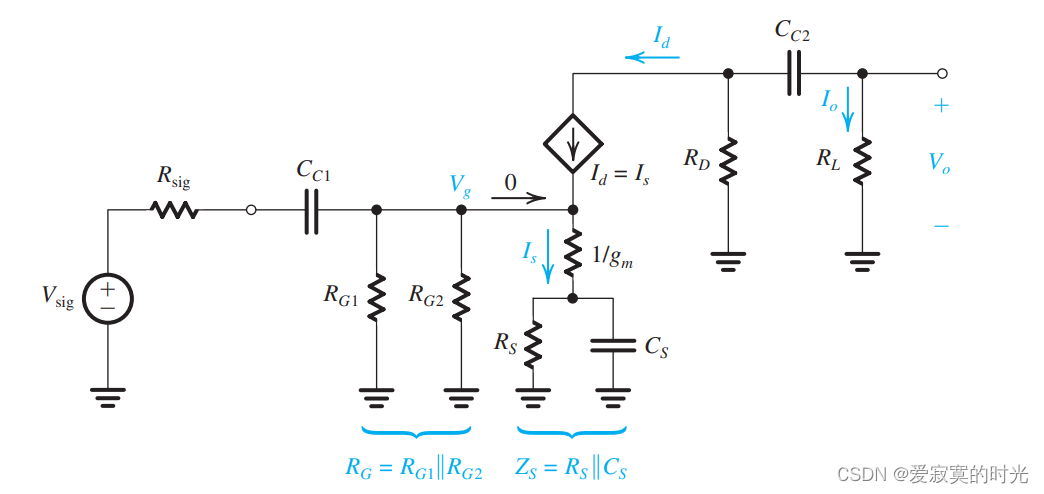
上图中，我们将 $V_{DD}$ 短路，并且将MOS使用T模型替代。为了计算 $V_o/V_{sig}$ 我们使用下面的链式模型：

$$\frac{V_o}{V_{sig}}=\frac{V_g}{V_{sig}}\times \frac{I_d}{V_g}\times \frac{V_o}{I_d}$$

这里 $V_g$ 是栅极电压， $I_d$ 是漏极电流。我们发现 $V_g$ 可以通过分压定律计算：

$$V_g=V_{sig}\frac{R_G}{R_G+\frac{1}{s{C}_{C1}}+R_{sig}}$$

这里的 $R_G$ 是CS的输入阻抗为：

$$R_G=R_{G1}||R_{G2}$$

而 $s$ 是拉普拉斯变换中的复频率，以后我们都使用 $s$ 表示复频率：

$$s=j\omega$$

则重新排列：

$$\frac{V_g}{V_{sig}}=\frac{R_G}{R_G+R_{sig}}\frac{s}{s+\frac{1}{C_{C1}(R_G+R_{sig})}}$$

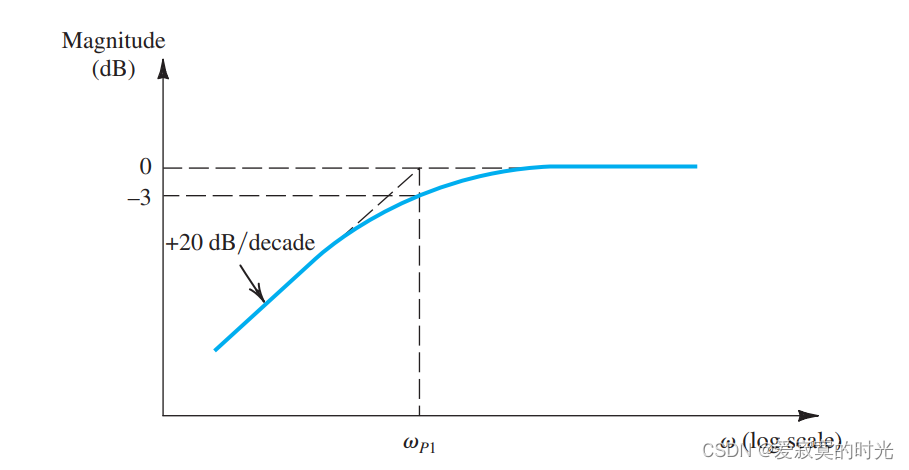
因此，我们发现 $C_{C1}$ 在信号从信号源到MOS的栅极引入了频率相关因子。我们知道这个因子是单时间常数电路中高通型传递函数，具有极点频率：

$${\omega }_{P1}=\frac{1}{C_{C1}(R_G+R_{sig})}$$

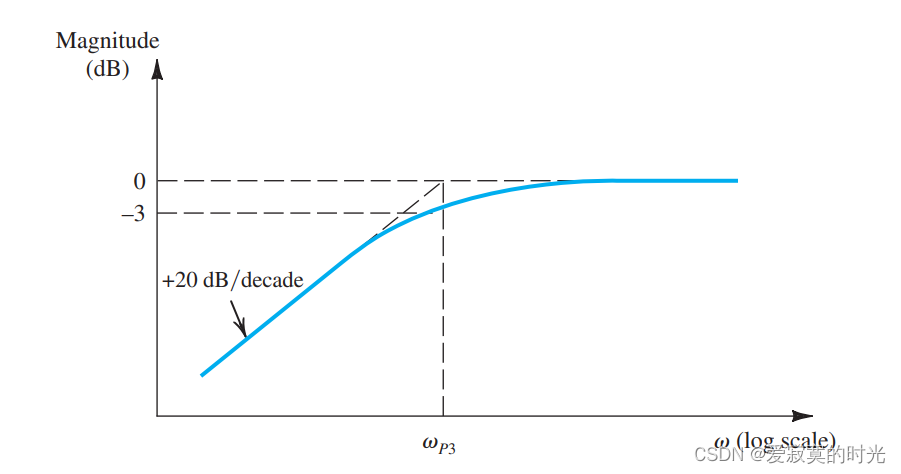
当 $s=0$ 的时候， $C_{C1}$ 引入了零因子。这是很显然的，因为电容具有阻直流的性质，下图描述了函数 $\frac{s}{s+{\omega }_{P1}}$ 的频率响应波德图：

继续我们的 $I_d$ 分析，因为 $I_d=I_s$ 后者可以通过电压比源极阻抗算出来：

$$I_d=I_s=\frac{V_g}{\frac{1}{g_m}+Z_S}=g_m{V}_g\frac{Y_S}{g_m+Y_S}$$

这里：

$$Y_S=\frac{1}{Z_S}=\frac{1}{R_S}+s{C}_S$$

写出多项式分式的形式：

$$\frac{I_d}{V_g}=g_m\frac{s+\frac{1}{C_S{R}_S}}{s+\frac{g_m+1/R_S}{C_S}}$$

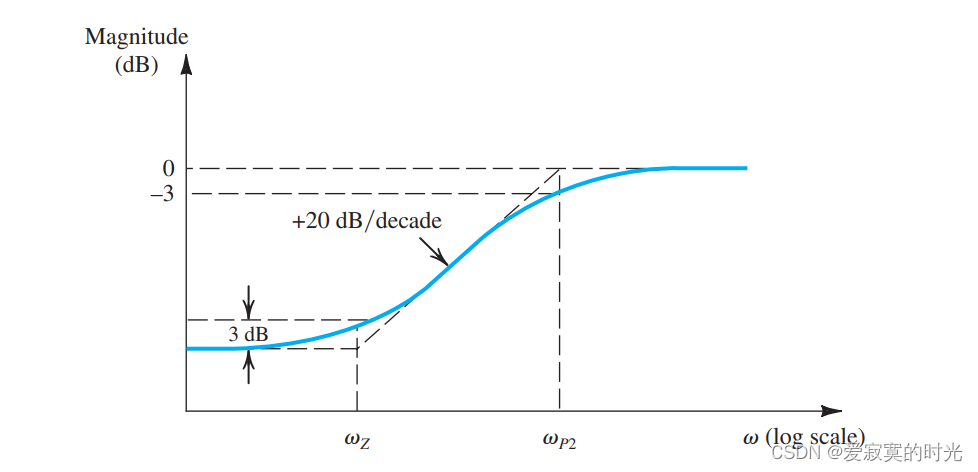
也就是说，旁路电容引入了极点频率：

$${\omega }_{P2}=\frac{g_m+1/R_S}{C_S}$$

以及一个零点：

$$s_Z=-\frac{1}{C_S{R}_S}$$

对应的零点频率为：

$${\omega }_Z=\frac{1}{C_S{R}_S}$$

下图展示了这个传递函数的频率响应图像：

因为 $g_m$ 很大，所以 ${\omega }_{P2}>{\omega }_Z$ 所以 ${\omega }_{P2}$ 更加靠近中频带，对 ${\omega }_L$ 的影响比 ${\omega }_Z$ 大。

最后，计算：

$$\frac{V_o}{I_d}=-\frac{R_D{R}_L}{R_D+R_L}\frac{s}{s+\frac{1}{C_{C2}(R_D+R_L)}}$$

耦合电容 $C_{C2}$ 引入极点频率：

$${\omega }_{P3}=\frac{1}{C_{C2}(R_D+R_L)}$$

以及零点 $s=0$ （DC）。频率响应如下：

则整体低频响应函数为：

$$\frac{V_o}{V_{sig}}=-\frac{R_G}{R_G+R_{sig}}{g}_m(R_D||R_L)(\frac{s}{s+{\omega }_{P1}})(\frac{s+{\omega }_Z}{s+{\omega }_{P2}})(\frac{s}{s+{\omega }_{P3}})$$

也就是：

$$\frac{V_o}{V_{sig}}=A_M(\frac{s}{s+{\omega }_{P1}})(\frac{s+{\omega }_Z}{s+{\omega }_{P2}})(\frac{s}{s+{\omega }_{P3}})$$

这里 $A_M$ 为完美增益，即不考虑任何频率特性的增益系数，也是我们之前几章使用过的：

$$A_M=-\frac{R_G}{R_G+R_{sig}}{g}_m(R_D||R_L)$$

当 $s=j\omega$ 远大于 ${\omega }_{P1},{\omega }_{P2},{\omega }_{P3},{\omega }_Z$ 的时候，此时 $A_v\simeq A_M$ 这个时候放大器进入中频带。

决定 $3-dB$ 频率 $f_L$

有了上述推导出的公式，我们就可以确定CS放大器的中频带的低频结束点，当 $|V_o/V_{sig}|$ 降至 $|A_M|/\sqrt{2}$ 的时候此时增益下降 $3dB$ ，记为 $f_L$ 。

有一个更简单的方式估算频率 $f_L$ ，当所有的极点和零点分的足够开的时候，我们可以使用博德规则，整体博德图如下：

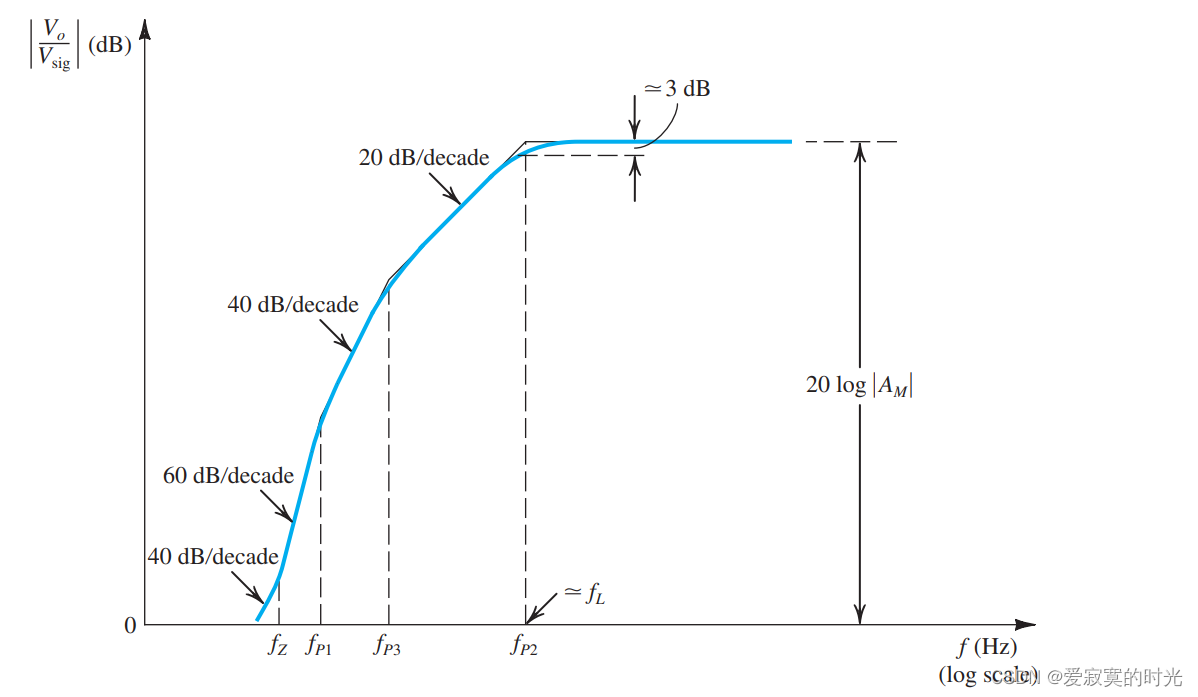
上图中，一般情况下都是 $f_{P2}$ 最大。一个快速的估算方法为：若最高极点频率 $f_{P2}$ 至少是最近的极点、零点频率 $f_{P3}$ 的4倍（2个8度）。则 $f_L$ 大约是最高极点频率。

$$f_L=f_{P2}$$

此时这种情况下，我们称最高极点频率为 主导极点 。

如果主导极点不存在，可以使用下面的表达式估算：

$$f_L\simeq \sqrt{f_{P1}^2+f_{P2}^2+f_{P3}^2-2f_Z^2}$$

通过观察决定极点和零点频率

因为在CS放大器中，各个电容是相互独立的，因此存在一个更简单的方法确定每一个电容的极点和零点频率。

首先是零点。传递函数的传输零点在 $s$ 使得 $V_o=0$ 的时候。在CS放大器中， $C_{C1}$ 在 $s=0$ 的时候具有无穷大阻抗因此引入了传输零点。

对于 $C_{C2}$ 也具有相同的结论。然而，对于旁路电容 $C_S$ 则具有不同的效果：根据定义传输零点在 $s$ 使得 $Z_S=\infty$ 的时候，此时 $s_Z=-\frac{1}{C_S{R}_S}$ 。

对于极点，我们令 $V_{sig}=0$ 此时电路可以拆成下面三个电路：

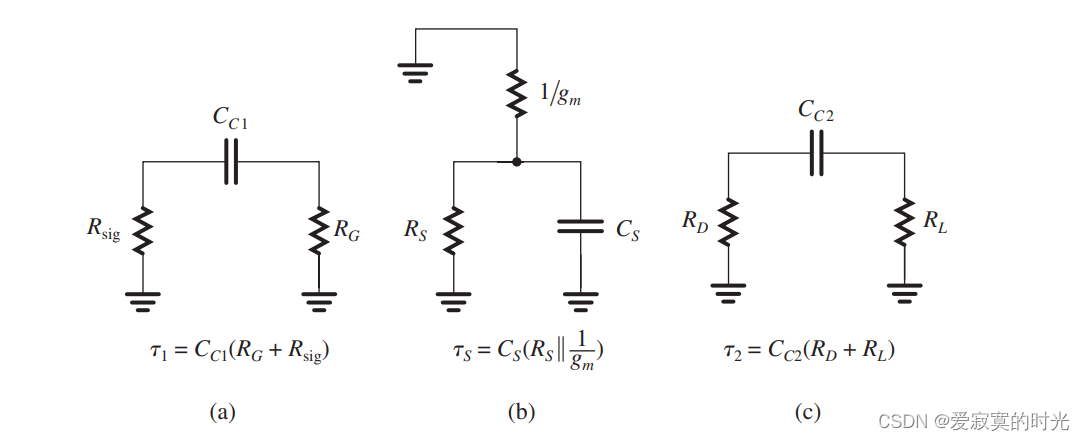
我们发现每一个电路都是单时间常数电路，时间常数为每个电容的容值乘以从该电容看过去的阻值，其对应的极点频率正好的每一个单时间常数的倒数。

耦合电容和旁路电容的选值

我们现在解决如何选择三个电容的容值，我们的最终目标是将 $f_L$ 设定在我们想要的值上同时最小化三个电容的容值。因为从 $C_S$ 看过去的阻值 $\frac{1}{g_m}||R_S$ 是三个里面最小的，总容抗可以通过选择 $C_S$ 来提供一个最高的极点频率来最小化，也就是令 $f_{P2}=f_L$ 。之后我们决定后两个极点频率，都是小于 $f_{P2}$ 5到10倍的。然而，$f_{P1}$ 和 $f_{P3}$ 也不能设置的太小，因为这需要更大的 $C_{C1},C_{C2}$ 。

短路时间常数法

在一些电路中，例如我们即将要讨论的CE放大器电路，电容并不是相互独立的，此时决定极点频率是比较困难的。幸好，存在一个简单的方法用来估算 $f_L$ ，这个方法不需要计算极点频率。尽管这个方法需要建立在存在一个主导极点频率的前提下，但是在前提不是那么严格的情况下也能获得不错的结果。方法是：

1. 令输入信号源 $V_{sig}=0$ 。
2. 依次考虑每一个电容。就是说，当考虑电容 $C_i$ 的时候，将其他电容看成是容值无穷大的电容，即短路状态。
3. 对于每一个电容，计算从这个电容看过去的总阻值 $R_i$ 这可以通过戴维南定理计算。
4. 则 $f_L={\sum }_{i=1}^n\frac{1}{C_i{R}_i}$

这个方法揭示了每个电容对 $f_L$ 的贡献。

CE放大器

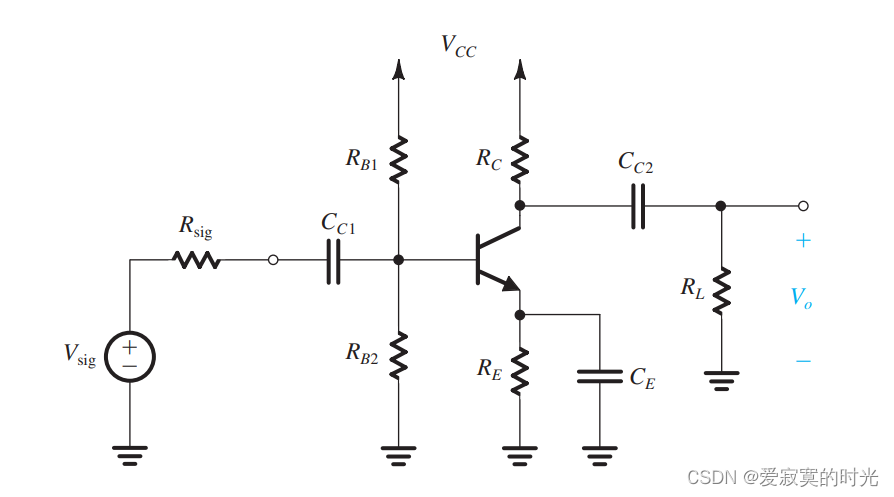
下图展示了一个完整的CE放大器的原理图：

为了分析低频响应，我们使用下面的等效电路：

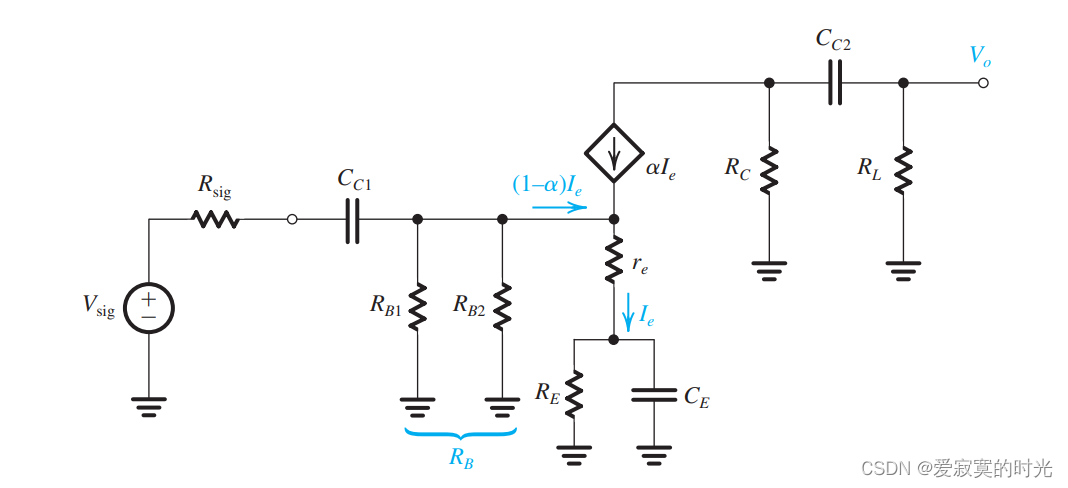
我们发现，因为存在有限的基极电流，电容 $C_{C1}$ 和 $C_{C2}$ 不是相互独立的。也就是说，不像CS放大器，每一个极点频率都和这两个电容有关，这给我们设计电路造成了不小的困难。因此，我们不想计算极点频率，而是转手使用短路时间常数法。

将信号输入源置地，然后依次考虑每个电容，如下图：

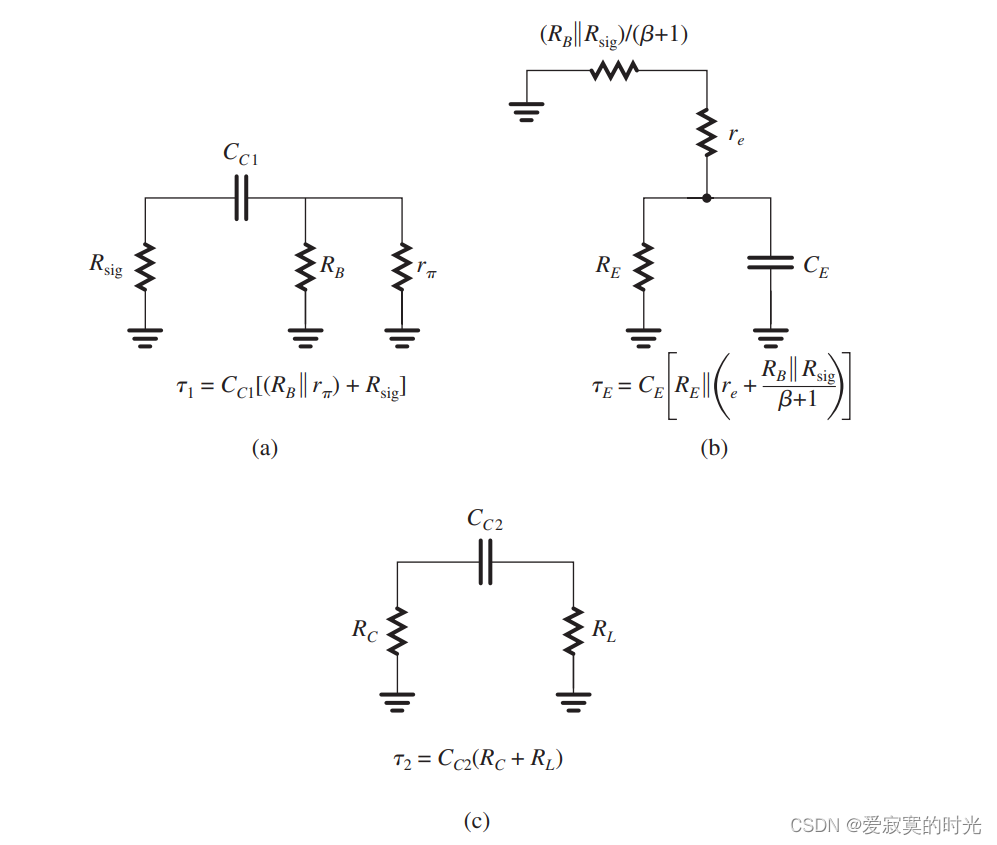
所有的时间常数我们都已经标在图中，因此估算的 $f_L$ 为：

$$f_L=\frac{1}{2\pi }[\frac{1}{C_{C1}{R}_{C1}}+\frac{1}{C_E{R}_E}+\frac{1}{C_{C2}{R}_{C2}}]$$

这个式子揭示了每个电容对 $f_L$ 的贡献。也就是具有最小时间常数的对 $f_L$ 的贡献最大，换句话说，就是 $C_E$ 贡献最大，因此 $C_E$ 是我们的主导极点频率。通常计算我们都假设 $C_E$ 对 $f_L$ 贡献 $80\%$ 而其他两项贡献 $20\%$ 。