二叉树讲解

对于二叉树，是真正的很难！很难，不是一般的难度！！

笔者学习完二叉树，笔记记录了得有三十多页，但是，还是很不理解（做题不怎么会）

下面进入二叉树的基础部分：

二叉树概念！！

一颗二叉树是节点的一个有限集合：该集合

或者为空

或者是由一个根节点加上两颗别称为左子树和右子树的二叉树组成

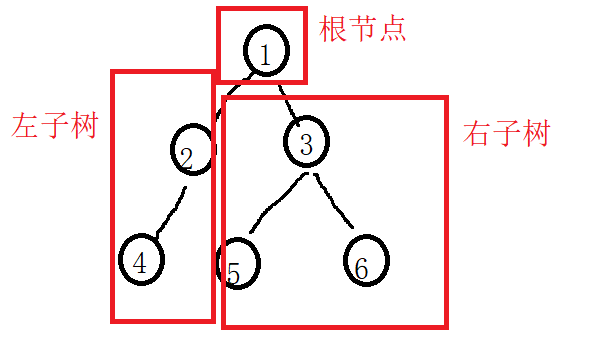
经过上述，我们可以得出：

二叉树不存在度大于2的节点（对于度是什么，不理解的读者，可以参考笔者的之前的文章：https://blog.csdn.net/weixin_64308540/article/details/129045341

二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树（左右顺序）

经过二叉树的上述内容的讲解，我们可以得出：对于任意类型的二叉树，都是由一下的几种情况复合而成的！

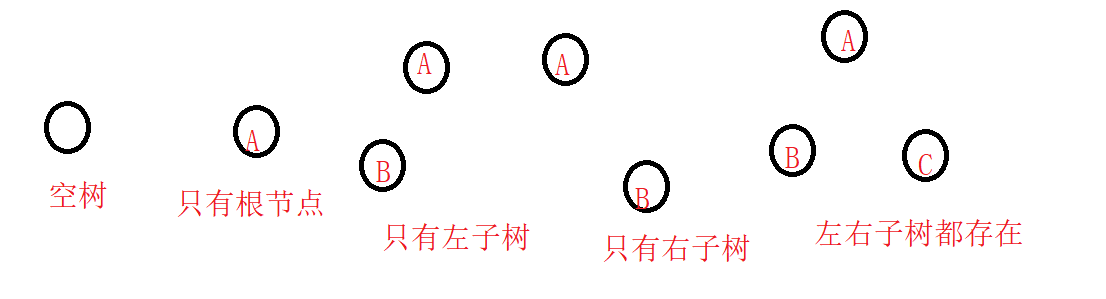
经过上述的内容，我们便可以根据自己的想法，设计任意类型的二叉树了！！

下面我们来进行讲解一下两种特殊的二叉树：

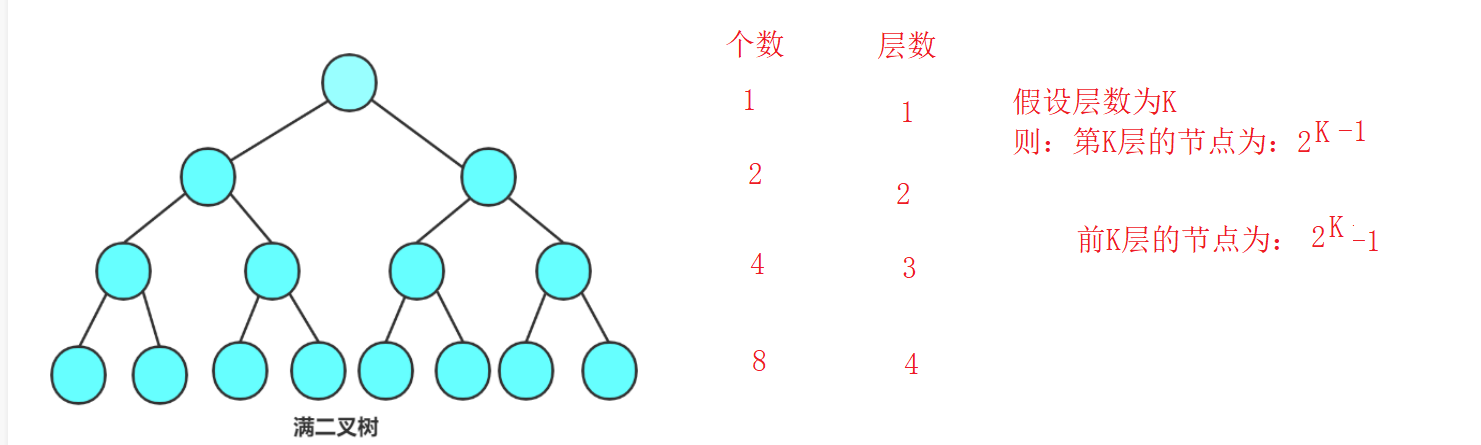
满二叉树: 一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是满二叉树。也就是说，如果一棵二叉树的层数为K，且结点总数是，则它就是满二叉树。

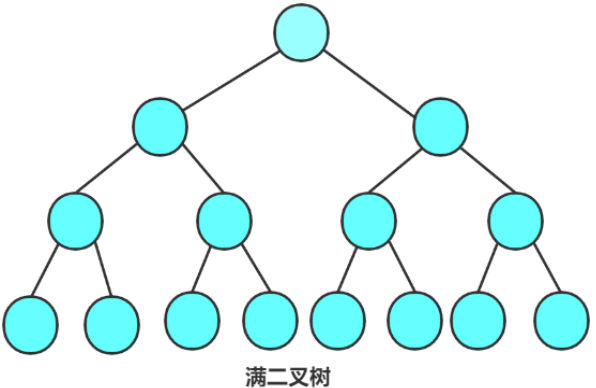
对于这个满二叉树，我们可以根据层数，每层的个数，最后得出节点的个数（考试可能会考）

完全二叉树: 完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

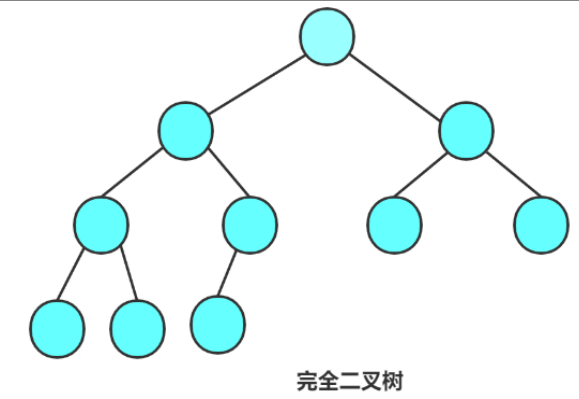
在这里，我们需要注意的是：满二叉树是一种特殊的完全二叉树

二叉树的性质！！

若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有 (i>0)个结点

若规定只有根结点的二叉树的深度为1，则深度为K的二叉树的最大结点数是 (k>=0)

具有n个结点的完全二叉树的深度k为上取整

对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i 的结点有： 1.若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点 2.若2i+1<n，左孩子序号：2i+1，否则无左孩子 3.若2i+2<n，右孩子序号：2i+2，否则无右孩子

对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0＝n2＋1

对于第5点，笔者在后续的代码/选择题/解答题当中，经常使用！所以，我们需要知道它的推理由来！！（笔者由一颗完全二叉树为列，来进行讲解）

根据上述的二叉树的性质，来做几个简单的练习题吧！！

. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ 200）提示：叶子节点为：度为0的节点（不知道度是什么的，可以参考：https://blog.csdn.net/weixin_64308540/article/details/129045341）

在具有 2n 个结点的完全二叉树中，叶子结点个数为（ n）

提示：2n是个偶数！！

思考一下：当奇数节点的时候，又会是怎么个结果？？思路跟刚才的一样！感兴趣的可以自己思考一下！

一个具有767个节点的完全二叉树，其叶子节点个数为（384）首先我们需要根据767（奇数），完全二叉树来进行思考！

一棵完全二叉树的节点数为531个，那么这棵树的高度为（ 10）

这个便不再解析了，大家自行解决！答案已经给出

二叉树的存储

二叉树的存储结构分为：顺序存储和类似于链表的链式存储。二叉树的链式存储是通过一个一个的节点引用起来的，常见的表示方式有二叉和三叉表示方式，

表示方式：

孩子表示法（比较常见）

class Node{
    int val;//数据域
    Node left;//左孩子的引用，常常代表左孩子为根的整根左子树
    Node right;//右孩子的引用，常常代表右孩子为根的整根右子树
}

孩子双亲表示法（后续平衡树时候，会用到）

class Node{
    int val;//数据域
    Node left;//左孩子的引用，常常代表左孩子为根的整根左子树
    Node right;//右孩子的引用，常常代表右孩子为根的整根右子树
    Node parent;//当前节点的根节点
}

学习了这么多！！有没有兴趣跟着笔者来手动创建一颗二叉树呢？？（不容拒绝哟！）

手动创建一颗二叉树吧！！

public class TestBinaryTree {
    static class TreeNode{
        public char val;//数据域
        public TreeNode left;//左孩子的引用
        public TreeNode right;//右孩子的引用

        public TreeNode(char val) {
            this.val = val;
        }
    }
    
    public TreeNode createTree(){
        TreeNode A=new TreeNode('A');
        TreeNode B=new TreeNode('B');
        TreeNode C=new TreeNode('C');
        TreeNode D=new TreeNode('D');
        TreeNode E=new TreeNode('E');
        TreeNode F=new TreeNode('F');
        TreeNode G=new TreeNode('G');
        TreeNode H=new TreeNode('H');

        A.left=B;
        A.right=C;
        B.left=D;
        B.right=E;
        C.left=F;
        C.right=G;
        E.right=H;
        
        return A;//A是跟节点
    }

    public static void main(String[] args) {
        TestBinaryTree testBinaryTree=new TestBinaryTree();
        TestBinaryTree.TreeNode root=testBinaryTree.createTree();
        System.out.println("成功的创建出来了一个二叉树！");
    }
}

根据上述的代码，我们在刚刚实列化节点的时候：

在最后，我们所创建的二叉树模型为：

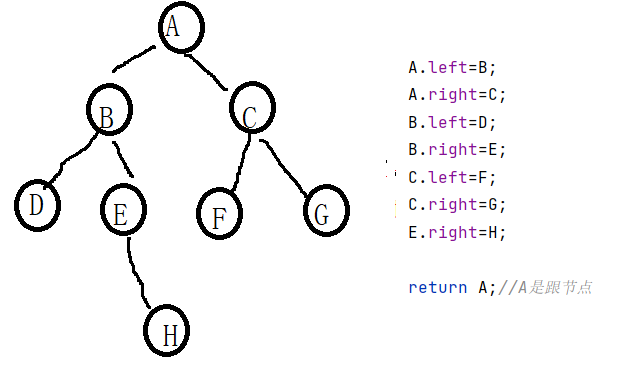
在这个代码中：当出了createTree方法之后，所创建的A,B,C,D,E,F,G,H,都会被回收掉了，但是创建好的A节点已经被return ，其所对应的关系不会被回收！！

二叉树的遍历

其实二叉树的遍历方式有前序遍历，中序遍历，后序遍历，还有层序遍历！！这些要求我们都得掌握！！加油！

从二叉树的递归定义可知：一颗非空的二叉树，由根节点及其左子树，右子树这三个部分组成的，因此，在任一给定节点上，可以按照某种次序执行三个操作：

访问节点本身（N）

遍历该节点的左子树（L）

遍历该节点的右子树（R）

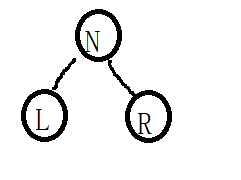
根据以上的思考，对于上述三种操作，我们可以有：NLR,LNR,LRN;NRL,RNL,RLN这六种操作，但是，需要注意的是：前面三种次序与后面三种次序相对称，故，我们只考虑前面的三种就可以了！！

遍历命名

根据访问节点操作发生的位置来命名！！

NLR：前序遍历！访问根节点的操作发生在遍历其左右子树之前（根左右）

LNR：中序遍历！访问根节点的操作发生在遍历其左右子树之间（左根右）

LRN：后序遍历！访问根节点的操作发生在遍历其左右子树之后（左右根）

对于前序遍历，中序遍历，后序遍历，的深层操作：

前序遍历（根左右）：若二叉树非空，则依次执行如下操作：1。访问根节点，2。遍历左子树，3.遍历右子树

中序遍历（左根右）：若二叉树非空，则依次执行如下操作：1。遍历左子树，2。访问根节点，3.遍历右子树

后序遍历（左右根）：若二叉树非空，则依次执行如下操作：1。遍历左子树，2。遍历右子树，3.访问根节点

层序遍历！！

所谓的层序遍历就是从所在二叉树的根节点出发，首先访问第1层的树根节点，然后从左到右访问第2层的节点，接着是第3层的节点，以此类推，自上而下，自左到右，逐层访问树的节点的过程，就是层序遍历！

根据前序遍历，中序遍历，后序遍历，层序遍历，来做几个小题吧！！

写出该二叉树的前序，中序，后序的遍历结果：

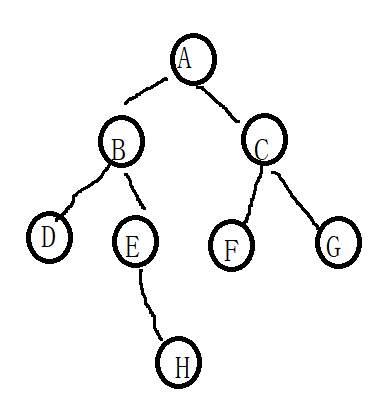
前序遍历：ABDEHCFG;

中序遍历: DBEHAFCG;

后序遍历: DHEBFGCA;

层序遍历: ABCDEFGH;

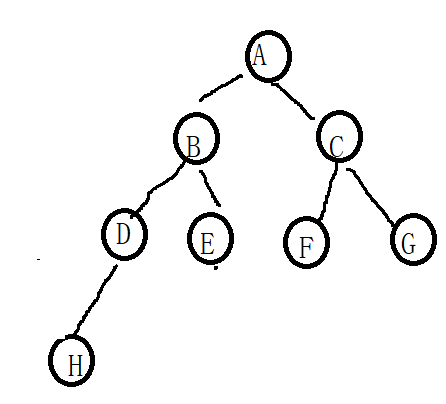
某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为(ABDFECFG) 根据层序遍历写出原始的二叉树即可！

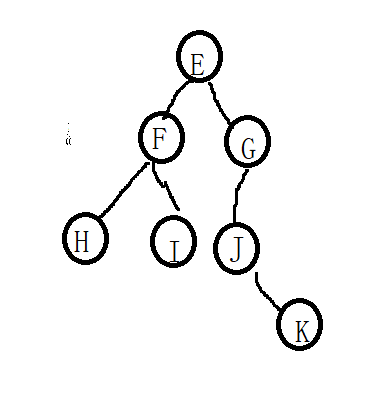
二叉树的前序遍历和中序遍历如下：先序遍历：EFHIGJK;中序遍历：HFIEJKG.则二叉树根结点为(E)

前序遍历的第一个节点就是根节点！！

中序遍历找到根的位置，左边就是左子树，右边就是右子树！！然后我们根据题意可以画出该二叉树！

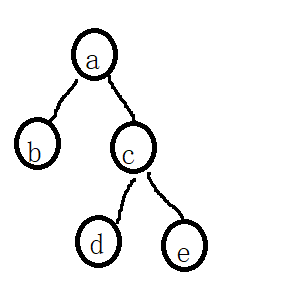
.设一课二叉树的中序遍历序列：badce，后序遍历序列：bdeca，则二叉树前序遍历序列为(abcde)

根据题意，我们可以得出，二叉树为：

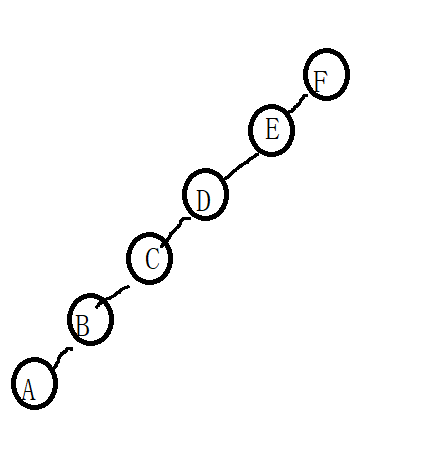
.某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出(同一层从左到右)的序列为(FEDCBA)

根据题意，我们可以得出，二叉树为：

经过了上述题目的洗涤，想必此时的你，已经对二叉树的前序遍历，中序遍历，后序遍历，层序遍历已经有着自己的思路了吧！！那么，接下来，我们便可以进入代码环节了！！

递归（前中后遍历）

前序遍历（根左右）递归

    //二叉树的前序遍历（递归）
    public void preOrder(TreeNode root){
        if (root==null){
            return;
        }
        System.out.print(root.val+" ");//根
        preOrder(root.left);//左
        preOrder(root.right);//右
    }

中序遍历（左根右）递归

   //二叉树的中序遍历（递归）
    public void inOrder(TreeNode root){
        if (root==null){
            return;
        }
        preOrder(root.left);//左
        System.out.print(root.val+" ");//根
        preOrder(root.right);//右
    }

后序遍历（左右根）递归

 //二叉树的后序遍历（递归）
    public void postOrder(TreeNode root){
        if (root==null){
            return;
        }
        preOrder(root.left);//左
        preOrder(root.right);//右
        System.out.print(root.val+" ");//根
    }

二叉树的基本操作

对于二叉树的基本操作有很多！希望尽可能多的去全面理解，消耗！

    // 获取树中节点的个数
    int size(Node root);
    // 获取叶子节点的个数
    int getLeafNodeCount(Node root);
    // 子问题思路-求叶子结点个数
    
   // 获取第K层节点的个数
    int getKLevelNodeCount(Node root,int k);
    // 获取二叉树的高度
    int getHeight(Node root);
    // 检测值为value的元素是否存在
    Node find(Node root, int val);
    //层序遍历
    void levelOrder(Node root);
    // 判断一棵树是不是完全二叉树
    boolean isCompleteTree(Node root);

下面便带领大家走进二叉树的基本操作环节！！更加深读！！

获取树中节点的个数（左节点+右节点+根节点）

方法1：

   //获取树中节点的个数（左节点+右节点+根节点）
    public int size(TreeNode root){
        if (root==null){
            return 0;
        }
        int leftSize=size(root.left);
        int rightSize=size(root.right);
        return leftSize+rightSize+1;
    }

方法2：

    public  int nodeSize;//成员变量

    public void size2(TreeNode root){
        if (root==null){
            return;
        }
        nodeSize++;//每遇到一个节点就++
        size2(root.left);
        size2(root.right);
    }

获取叶子节点的个数（子思路问题）

方法1：

   //获取叶子节点的个数（子思路问题）
    int getLeafNodeCount(TreeNode root){
        if (root==null){
            return 0;
        }
        if (root.left==null && root.right==null){
            return 1;
        }
        int leftSize=getLeafNodeCount(root.left);
        int rightSize=getLeafNodeCount(root.right);
        return leftSize+rightSize;
    }

方法2：

 public int leafSize;
    void getLeafNodeCount2(TreeNode root){
        if (root==null){
            return;
        }
        if (root.left==null && root.right==null){
            leafSize++;
        }
        getLeafNodeCount2(root.left);
        getLeafNodeCount2(root.right);
    }

获取第K层节点的个数

  //获取第K层节点的个数
    int getKLevelNodeCount(TreeNode root,int k){
        if (root==null){
            return 0;
        }
        if (k==1){
            return 1;
        }
        int leftSize=getKLevelNodeCount(root.left,k-1);
        int rightSize=getKLevelNodeCount(root.right,k-1);
        return leftSize+rightSize;
    }

获取二叉树的高度

方法1：

   //获取二叉树的高度
    public int getHeight(TreeNode root){
        if (root == null) {
                return 0;
            }
        return (getHeight(root.left)>(getHeight(root.right))?(getHeight(root.left)+1 ): (getHeight(root.right)+1));
    }

方法2：

   public int getHeight2(TreeNode root){
        int leftHeight=getHeight2(root.left);//左数的高度
        int rightHeight=getHeight2(root.right);//右数的高度
        return (leftHeight>rightHeight)?(leftHeight+1):(rightHeight+1);
    }

检测值为value的元素是否在二叉树中

    //检测值为value的元素是否在二叉树中
    TreeNode find(TreeNode root,int val){
        if (root==null){
            return null;
        }
        if (root.val==val){
            return root;
        }
        //左子树找到
        TreeNode leftTree=find(root.left,val);
        if (leftTree!=null){
            return leftTree;
        }
        //右子树找到
        TreeNode rightTree=find(root.right,val);
        if (rightTree!=null){
            return rightTree;
        }
        //都没有找到
        return null;
    }

上述的二叉树的基本操作，笔者没有实现完成，主要原因还是在于：剩下没有写的那些操作，基本都是题目了！！所以，我们可以通过系统的练习，来加深印象！！

感兴趣的可以看一下笔者的后续二叉树文章！！