从TransE到TransH模型

在之前知识图谱模型中，我们介绍了TransE模型的基本原理，对于TransE模型其基本原理为：
$$h+r=t$$

其中$h$是头实体向量，$r$是关系向量，$t$是尾实体向量。根据这个核心公式，我们不难发现其存在一定的局限性。比如当存在多对一关系的时候，假设$(h_1,r,t)$,$(h_2,r,t)$。根据TransE假设，可以确定的是：
$$h_1+r=t,h_2+r=t$$
这里$h_1,h_2$两个头实体的向量过于相近，与此同时，当存在$(h,r,t)$,$(t,r,h)$均在图谱中出现的时候，会计算出$r=0,h=t$.
总之来说，TransE模型在处理多对一， 多对多，自反关系的时候，会有很多局限性。为了解决上面我们提到的问题，衍生出TransH模型。

TransH基本思想

基本思想

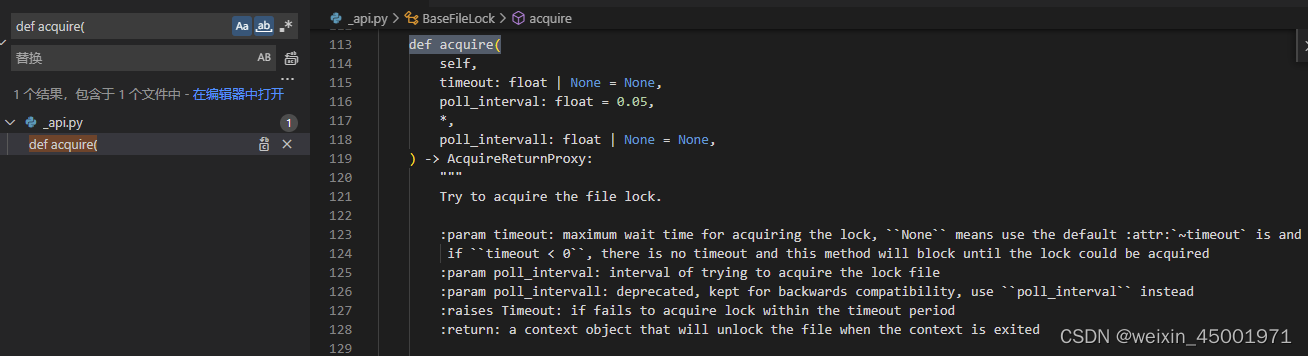
针对每个关系$r$,都给出一个超平面$wr$,在$wr$超平面上定义关系向量$dr$,将原有的头实体$h$和尾实体$t$映射到超平面为$hr$和$tr$.要求正确的三元组满足下面公式:
$$hr+dr=tr$$
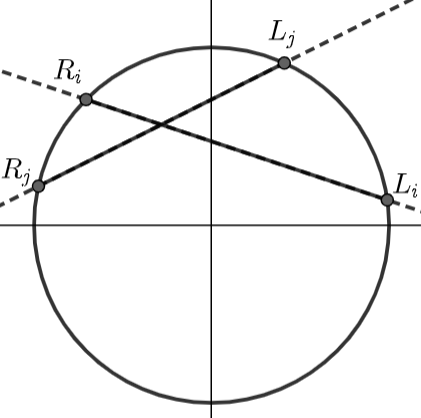
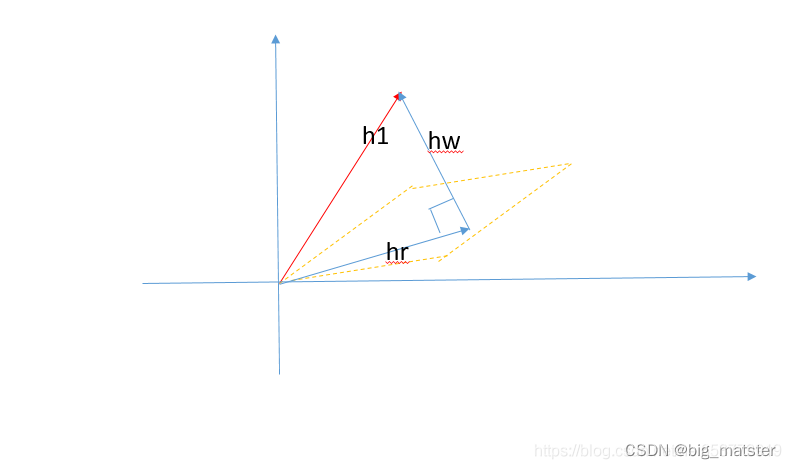
用一张图来表示这个过程：

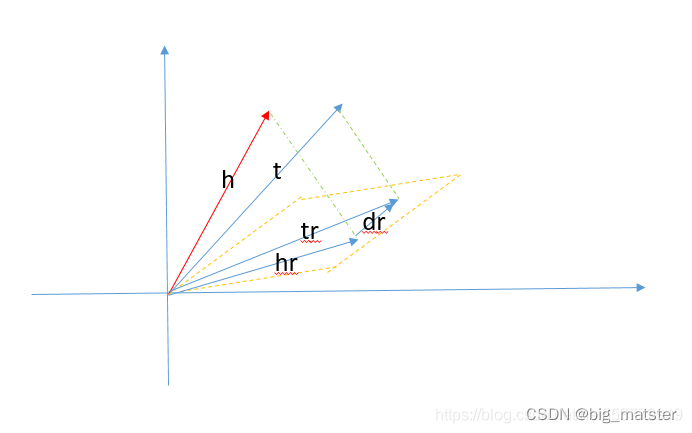
基于TransE改进

我们之前提到了，在TransE模型中，如果$h1$和$h2$向量都存在着同一关系$r$和同一尾实体$t$.那么在TransE中$h1$和$h2$是相同的。（或者可以说是特别近似的）
而在TranH中，如果对于$h1,h2$向量都存在一个三元组$(h1,r,t)和(h2,r,t)$。通过TranH关系$r$的超平面映射。则有:
$$h_{1r}+dr=tr$$
$$h_{2r}+dr=tr$$

也就是说$h1,h2$在超平面的映射是形同的或者近似的，但是对于$h_1,h_2$本身可以是不相近的，也就是可以区分的，如下图所示：

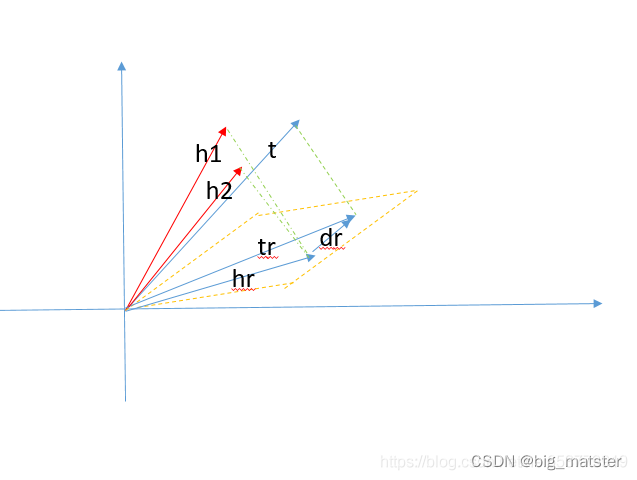
解决多对一关系的。

数学推导

首先，我们假设$w$为关系平面$wr$的单位法向量。在原始向量$h$在法向量$w$上的投影长度为：
$$|w|\ast |h|\ast cos(\theta )$$
整理成向量的形式为：

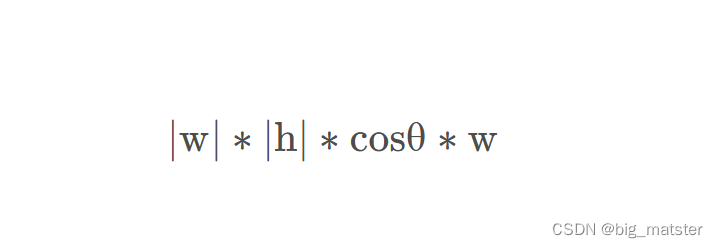
其中，一定要注意$w$是单位法向量。
也就是说，原始向量$h$在关系平面$wr$上的单位法向量的投影为:
$$h_w=w^{T}hw$$

则，我们可以确定对于映射向量$hr$有:
$$h_r=h-h_w=h_r-w^{T}hw$$
同理，我们可以确定有：
$$t_w=w^{T}tw$$
$$t_r=t-t_w=t-w^{T}tw$$
然后我们回一下，TransE目标函数为：

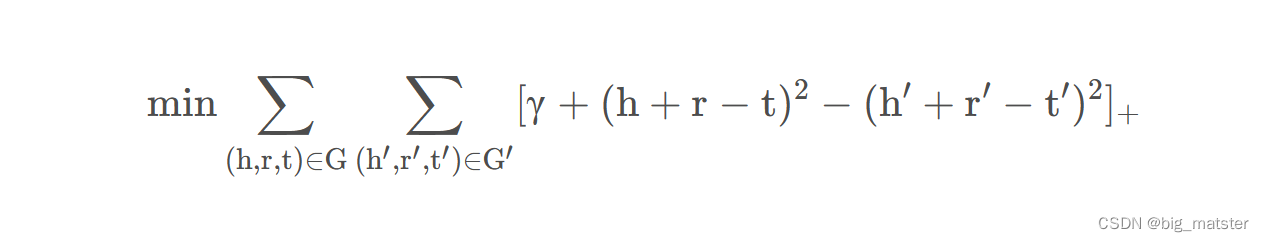
这里我们采用的是$L2$范数，（欧氏距离）。在TransH中，我们也采用这种方式，有兴趣的读者可以采用其他距离来计算。
与TransE函数目标类似，我们希望的是最小化在关系平面上的正确三元组的距离差，最小化错误三元组的距离差的相反数。也就是：



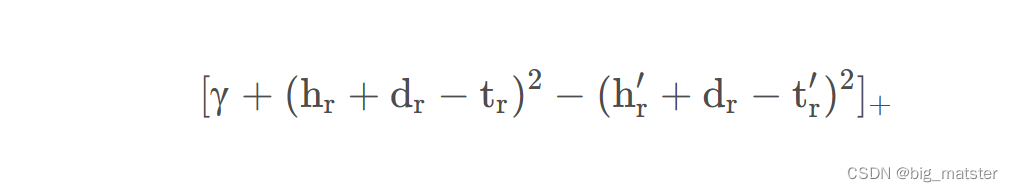
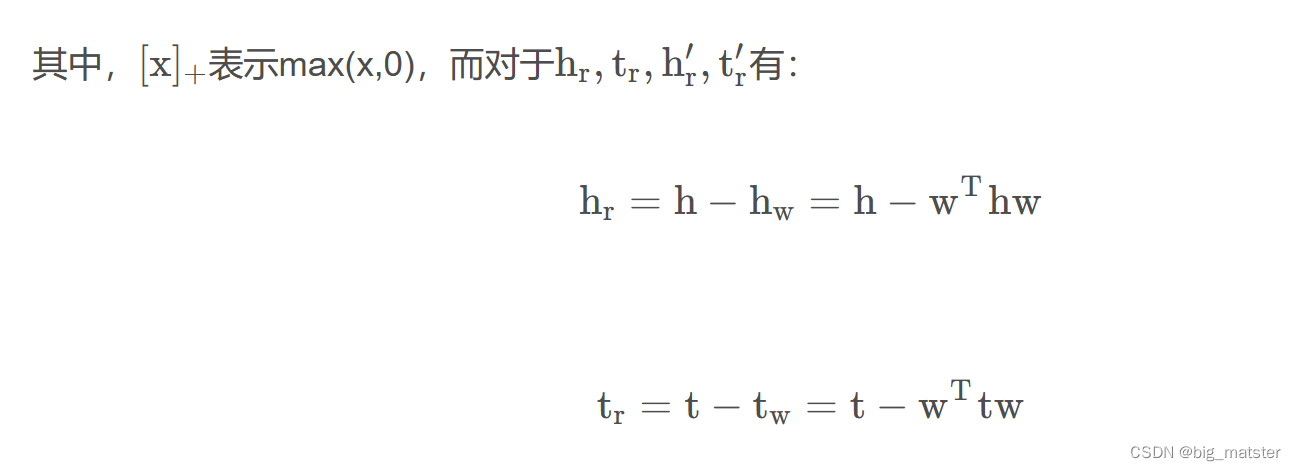
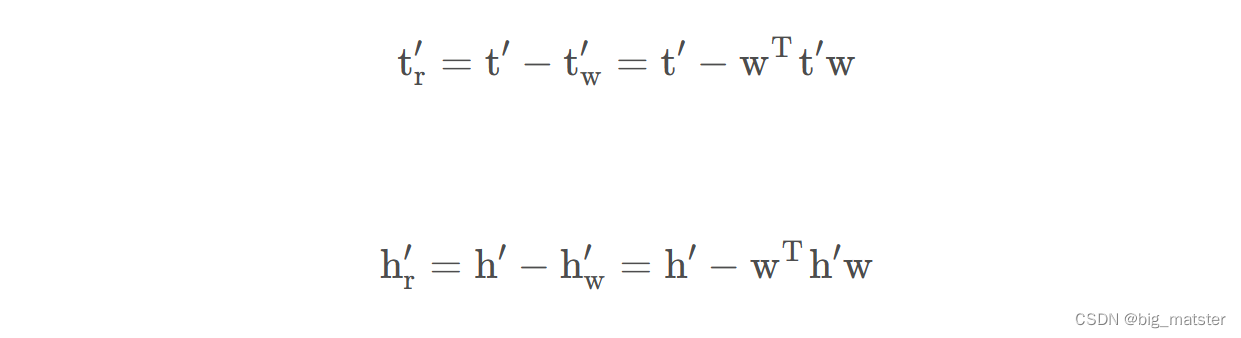
则可以定义总的目标函数为：
损失函数，以及根据loss函数对参数进行求导，则公式定义为：
目标函数，总损失函数以及求导公式参考

论文上有关TransH知识

经验:

后续自己将损失函数都给其推导以下，将其全部都推导以下都行啦的样子与打算，会自己将其推导一遍，。

会自己将求导公式推导一遍。全部都整理完整都行啦的回事与打算。