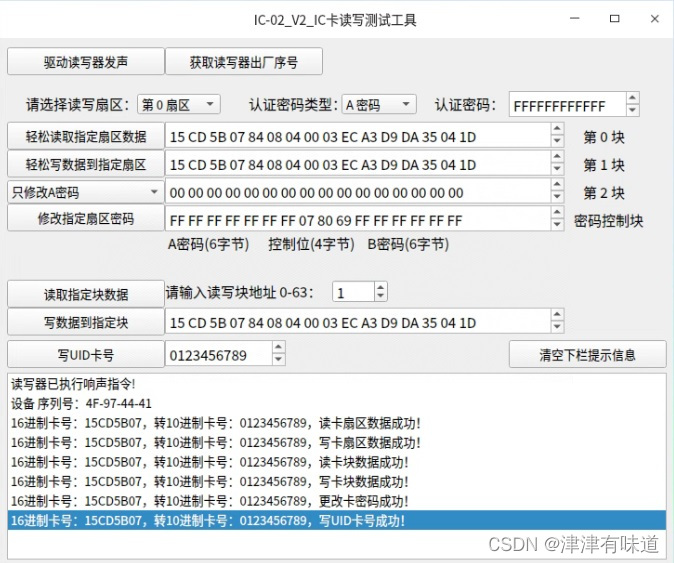
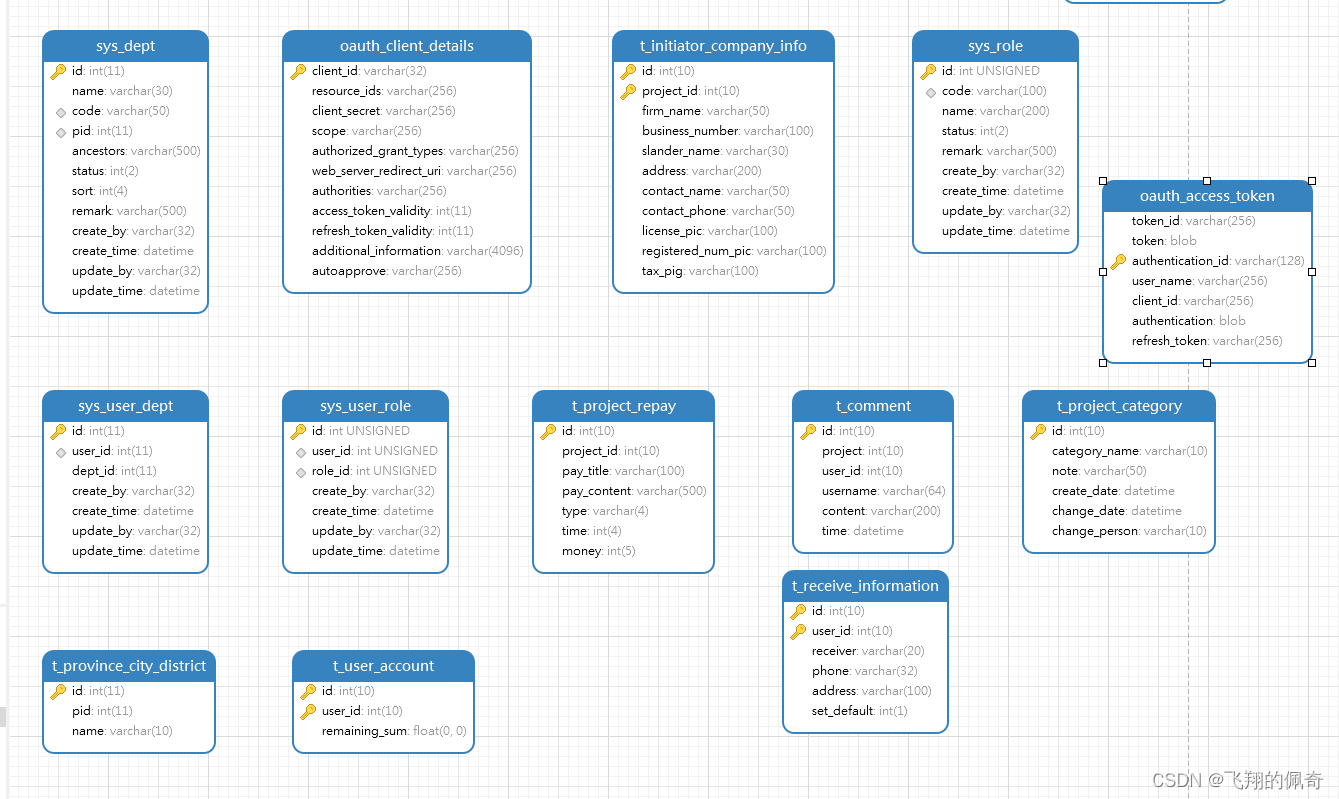
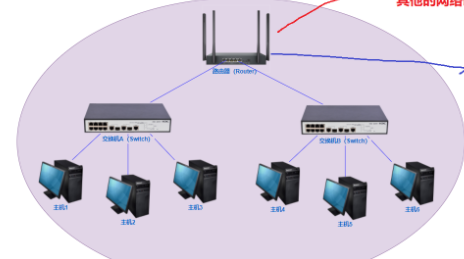
第五章.与学习相关技巧
5.2 权重初始值
本节将介绍权重初始值的推荐值,并通过实验确认神经网络的学习是否会快速进行。
1.权值衰减
- 权值衰减就是一种以减少权重参数的值为目的进行学习的方法,通过减少权重参数值来抑制过拟合的情况发生。
2.权重初始值不可设为相同值的原因
- 在误差反向传播法中,所有权重值都会进行相同的更新(乘法节点的反向传播原理),权重被更新为相同的值,这使得神经网络拥有许多不同的权重的意义就丧失了,为了防止权重均一化,必须随机生成初始值。
3.权重初始值的设置方法
1).随机初始值:
-
示例:
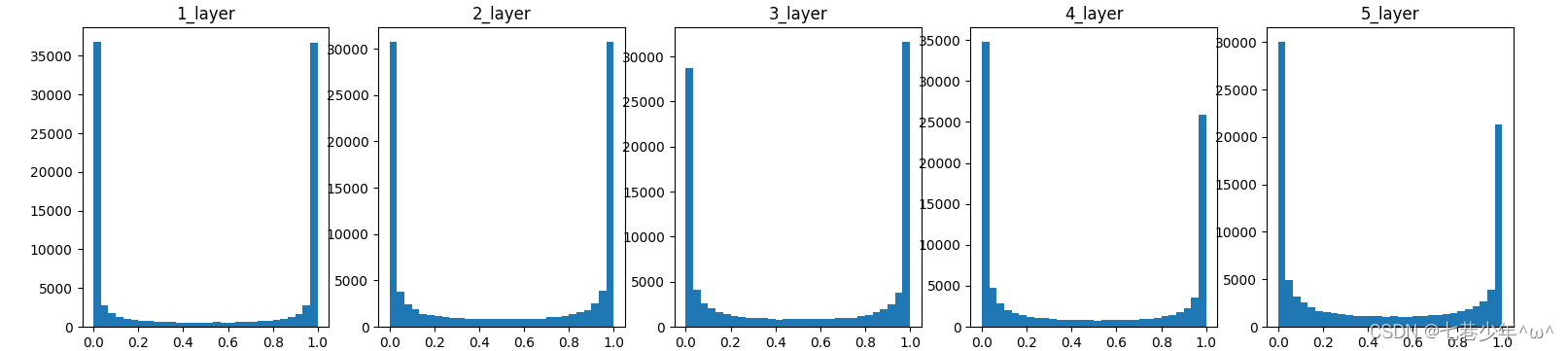
观察权重初始值是如何影响隐藏层的激活函数的分布:向一个5层神经网络(激活函数使用sigmoid函数)传入随机生成的输入数据,用直方图绘制各层激活值的数据分布(神经网络权重标准差设置为0.01或1的高斯分布情况)
-
各层激活值分布图:[标准差为1/0.01的高斯分布]
-
标准差为1的高斯分布
图像描述:各层的激活值呈偏向0/1的分布,这里使用的sigmoid是S型函数,随着输出不断的靠近0/1,它的导数值逐渐接近0,因此偏向0和1的数据分布会造成反向传播中梯度的值不断变小,最后消失,这个问题称为梯度消失。
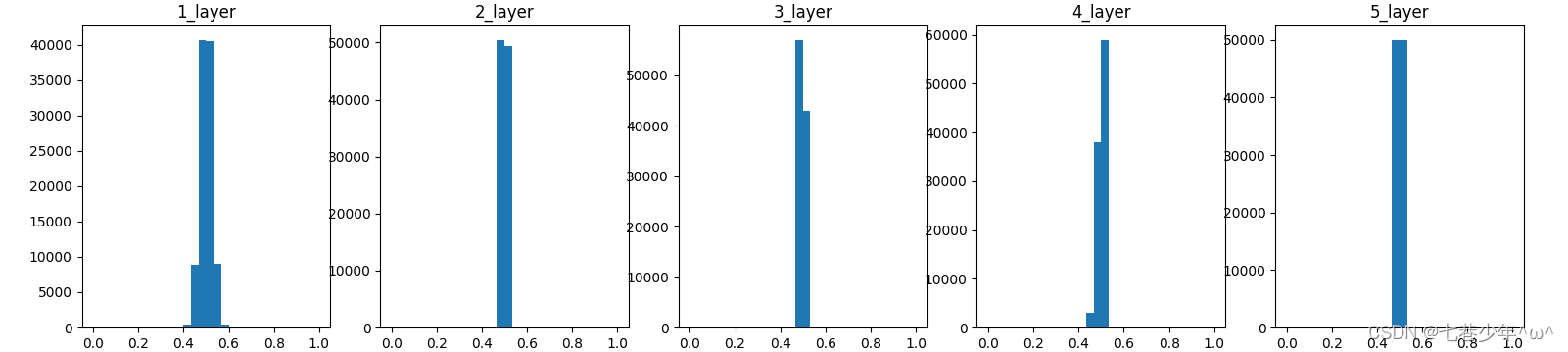
-
标准差为0.01的高斯分布
图像描述:这次集中在0.5附近的分布,不会像刚才的例子偏向0/1,所以不会出现梯度消失的问题,但是激活值的分布有所偏向,会出现“表现力受阻”的问题
-
-
各层激活值的分布特点:
各层激活值的分布都要求有适当广度的原因:通过在各层间传递多样性的数据,神经网络可以进行高效学习。反过来,如果传递的是有所偏向的数据,就会出现梯度消失或者表现力受阻的问题,导致学习可能无法顺利进行。
2).Xavier初始值:
-
示例:
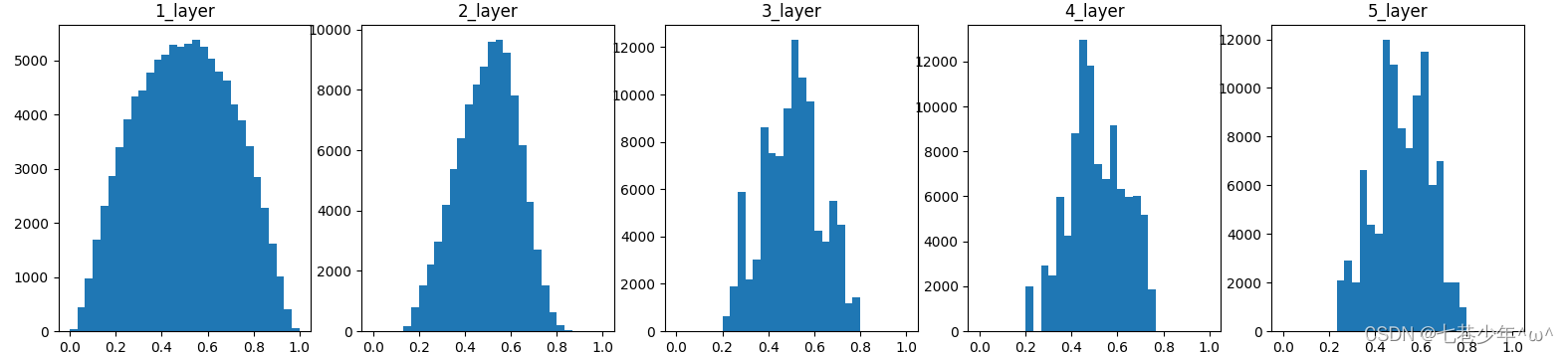
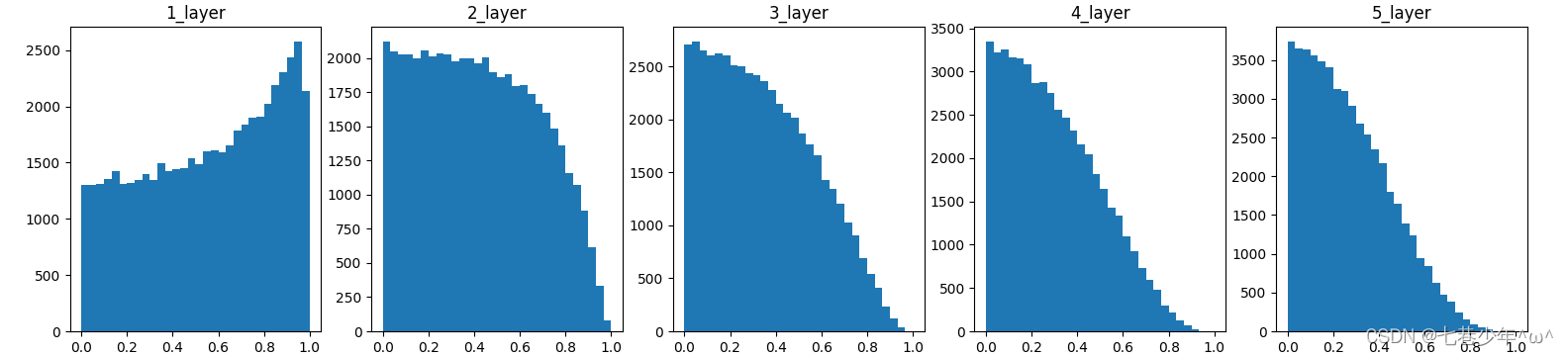
观察权重初始值是如何影响隐藏层的激活函数的分布:向一个5层神经网络传入随机生成的输入数据,用直方图绘制各层激活值的数据分布(神经网络权重标准差设置为1/√n的高斯分布情况)
-
各层激活值分布图:[标准差为1/√n的高斯分布]
-
激活函数:sigmoid
-
激活函数:tanh
-
-
图像描述:
sigmoid激活函数后面的层分布呈稍微歪斜的形状,如果是tanh激活函数,这个稍微倾斜的问题就会得到改善。众所周知,用作激活函数的函数最好具有关于原点对称的性质。[tanh函数:关于原点(0,0)对称的S型曲线;sigmoid函数:关于(x,y)=(0,0.5)对称的S型曲线] -
结论:
如果前一层的节点数为n,则初始值使用标准差为1/√n的分布。
3).He初始值:(ReLU激活函数专用初始值)
-
示例:
观察权重初始值是如何影响隐藏层的激活函数的分布:向一个5层神经网络传入随机生成的输入数据,用直方图绘制各层激活值的数据分布(神经网络权重标准差设置为√(2/n)的高斯分布情况)
-
各层激活值分布图:[标准差为√(2/n)的高斯分布]
- 激活函数:ReLU
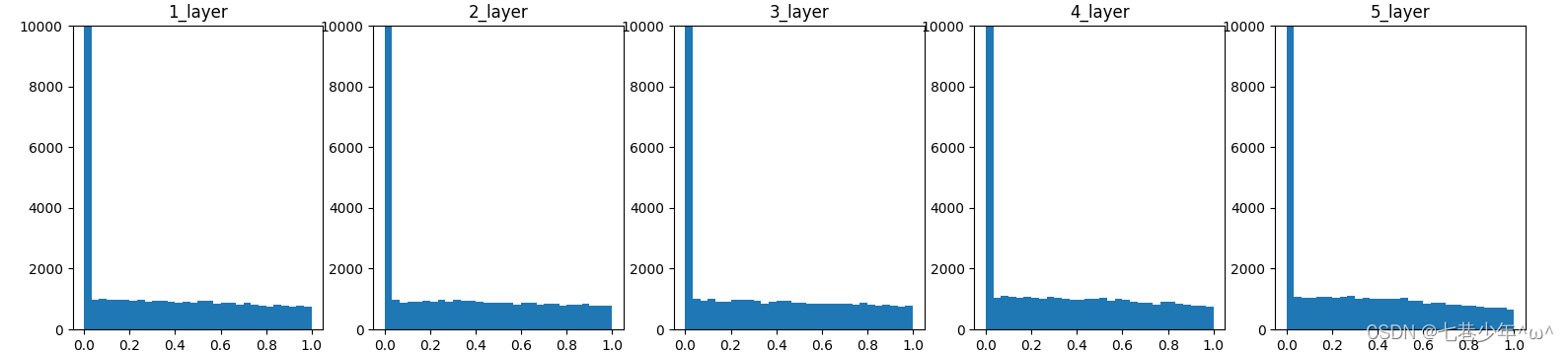
- 激活函数:ReLU
-
图像描述:
当初始值为He初始值时,各层中分布的广度相同,即使层加深,数据的广度也能保持不变,因此逆向传播时,也会传递合适的值。 -
结论:
如果前一层的节点数为n,则初始值使用标准差为√(2/n)的分布。
4).总结
- 激活函数为ReLU时:权重初始值使用He初始值。
- 激活函数为sigmoid/tanh等S型曲线函数时:权重初始值使用Xavier初始值。
![表现良好的最长时段[前缀和思想子数组]](https://img-blog.csdnimg.cn/2888a91342774f1aad0fad201bbe61a4.png)
![[SCTF2019]babyre 题解](https://img-blog.csdnimg.cn/8bef6205304c45a79d57f3ff73a097bd.png)