2023csoj寒假训练10

news2024/11/18 6:43:52

csoj寒假训练10

A

并查集

两个黑球之间距离不够这个白球通过的话，视为一个集合

考虑怎样维护这样两两之间的关系，我们使用并查集

同时黑球与直线的关系也要做一次维护

最后可以直接判断是否上下两条直线是否在一个集合里面

如果在一个集合里面说明没有一条容许白球通过的通路

#include<iostream>
#include<stdio.h>
#define int long long
using namespace std;
const int N=5050;
int R,n,p[N],x[N],y[N],r[N],a,b;
int find(int x){
    if(p[x]==x)return x;
    return p[x]=find(p[x]);
}
int cal(int i,int j){
    int dx=abs(x[i]-x[j]);
    int dy=abs(y[i]-y[j]);
    return dx*dx+dy*dy;
}
void merge(int i,int j){
    p[find(i)]=find(j);
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    // freopen("15.in","r",stdin);
    // freopen("15.out","w",stdout);

    cin>>R>>a>>b>>n;
    for(int i=1;i<=n;i++)cin>>x[i]>>y[i]>>r[i];
    for(int i=1;i<=n;i++)p[i]=i;
    p[0]=0;p[n+1]=n+1;
    for(int i=1;i<=n;i++){
        if(abs(y[i]-a)<=R)merge(0,i);
        if(abs(y[i]-b)<=R)merge(n+1,i);
    }
    for(int i=1;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            int D=r[i]+r[j];
            if(cal(i,j)<=D*D)merge(i,j);
        }
    }
    if(find(0)==find(n+1))cout<<"NO";
    else cout<<"YES";
}

大家可以考虑一下如果让你求最大白球半径怎么做

B

签到题

只需要倒着做就好了

#include<iostream>
#include<vector>
#include<stdio.h>
using namespace std;
const int N=1e7+10;
int n,m,q,p[N],u[N],v[N],vis[N],op[N],val[N];
int del[N];
vector<int>ans;
int find(int x){
    if(p[x]==x)return x;
    return p[x]=find(p[x]);
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    // freopen("3.in","r",stdin);
    // freopen("3.out","w",stdout);
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)p[i]=i;
    for(int i=1;i<=m;i++)cin>>u[i]>>v[i],vis[i]=1;
    for(int i=1;i<=q;i++){
        cin>>op[i];
        if(op[i]==1){
            int x;
            cin>>x;
            val[i]=x;//第i次操作是删第x条边
            if(vis[x]==1){
                vis[x]=0;//第x条边被删了
                del[x]=i;//删掉第x条边是在第i次操作
            }
        }
    }
    for(int i=1;i<=m;i++){
        if(vis[i]){
            int a=u[i];
            int b=v[i];
            if(find(a)==find(b))continue;
            else p[find(a)]=find(b);
        }
    }
    int cnt=0;
    for(int i=1;i<=n;i++)if(find(i)==i)cnt++;
    for(int i=q;i>=1;i--){
        if(op[i]==1){
            int x=val[i];
            if(del[x]!=i)continue;
            int a=u[x];
            int b=v[x];
            if(find(a)==find(b))continue;
            else p[find(a)]=find(b),cnt--;
        }
        else ans.push_back(cnt);
    }
    for(int i=ans.size()-1;i>=0;i--)cout<<ans[i]<<'\n';
}

C

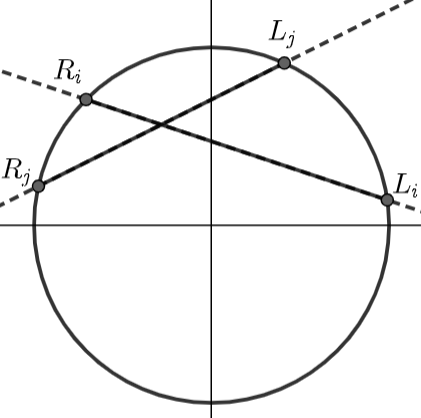
考虑二分答案，求区间内交点个数

如果直线与圆有交点的话，就把两个交点的极角保留下来

对所有的极角离散化，最后交点相当于求有多少个 有序对 ( i , j ) 满足 Li<=Lj<=Ri<=Rj

可以直接线段树或者树状数组做

img

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<math.h>
#include<bits/stdc++.h>
using namespace std;

const int N = 5e4 + 5;
const double eps = 1e-5;

int n, k, m, m2, ans, a[N], b[N], c[N], f[N << 1];
double v[N << 1];
struct Node { double l, r; }p[N];
struct Node2 { int l, r; }q[N];

inline void upd(int i, int x) {
    while (i <= m2) f[i] += x, i += (i & -i);
}
inline void qry(int i) {
    while (i) ans += f[i], i &= i - 1;
}

int calc(double r) {
    m = 0, m2 = 0, ans = 0;
    for (int i = 1; i <= n; ++i) { //处理直线
        int A = a[i], B = b[i], C = c[i];
        double d = (A * A + B * B) * r * r - C * C;
        if (d < 0) continue;
        d = sqrt(d);
        double tl = atan2(-B * C + A * d, -A * C - B * d);
        double tr = atan2(-B * C - A * d, -A * C + B * d);
        if (tl > tr) swap(tl, tr);
        v[++m2] = tl, v[++m2] = tr;
        p[++m] = { tl,tr };
    }
    sort(v + 1, v + m2 + 1);
    for (int i = 1; i <= m; ++i) { //离散化
        q[i].l = lower_bound(v + 1, v + m2 + 1, p[i].l) - v;
        q[i].r = lower_bound(v + 1, v + m2 + 1, p[i].r) - v;
    }
    sort(q + 1, q + m + 1, [](Node2 x, Node2 y) { return x.r < y.r; });
    memset(f, 0, sizeof f);
    for (int i = 1; i <= m; ++i) { //计算答案
        qry(q[i].l);
        upd(q[i].l + 1, 1);
        upd(q[i].r, -1);
    }
    return ans;
}

int main() {
    int t=1;
    //cin >> t;
    for (int i = 0; i < t; i++) {
        cin >> n >> k;
        for (int i = 1; i <= n; ++i)
            cin >> a[i] >> b[i] >> c[i];
        double l = 0, r = 3e6, mid;
        while (r - l > eps) { //二分
            mid = (l + r) / 2;
            calc(mid) < k ? l = mid : r = mid;
        }
        printf("%.6lf\n", r);
    }
    return 0;
}

#include<bits/stdc++.h>
#define y1 trcyvubinm
#define ls u<<1
#define rs u<<1|1
using namespace std;
#define int long long
const int N=5e4+10;
// const int N=1e5+10;
int n,k;
double A[N],B[N],C[N];
double L[N],R[N];
int o[N],ok[N];
struct node{
    int a[N*8];
    void init(){
        memset(a,0,sizeof a);
    }
    void pushup(int u){
        a[u]=a[ls]+a[rs];
    }
    void modify(int u,int x,int l=0,int r=n*2){
        if(l==r){
            a[u]++;
            return;
        }
        int mid=l+r>>1;
        if(x<=mid)modify(ls,x,l,mid);
        else modify(rs,x,mid+1,r);
        pushup(u);
    }
    int query(int u,int x,int l=0,int r=n*2){
        if(x>=r)return a[u];
        if(x<l)return 0;
        if(l==r)return 0;
        int mid=l+r>>1;
        return query(ls,x,l,mid)+query(rs,x,mid+1,r);
    }
}T[2];
typedef pair<double,double>PDD;
int tr[N*2];
void add(int x,int c=1){
    for(int i=x;i<2*N;i+=i&-i)tr[i]+=c;
}
int query(int x){
    int ans=0;
    for(int i=x;i;i-=i&-i)ans+=tr[i];
    return ans;
}
int check(double d){
    vector<double>v;
    T[0].init(),T[1].init();
    vector<PDD>S;
    for(int i=1;i<=n;i++){
        double D=C[i]*C[i];
        if(D>(A[i]*A[i]+B[i]*B[i])*d*d)continue;
        if(A[i]==0){
            double y1=-C[i]/B[i];
            double x1=-sqrt(d*d-y1*y1);
            double l=atan2(y1,x1);
            double y2=y1;
            double x2=sqrt(d*d-y1*y1);
            double r=atan2(y2,x2);
            if(l>r)swap(l,r);
            v.push_back(l);
            v.push_back(r);
            S.push_back({r,l});
            continue;
        }
        if(B[i]==0){
            double x1=-C[i]/A[i];
            double y1=-sqrt(d*d-x1*x1);
            double l=atan2(y1,x1);
            double x2=x1;
            double y2= sqrt(d*d-x2*x2);
            double r=atan2(y2,x2);
            if(l>r)swap(l,r);
            v.push_back(l);
            v.push_back(r);
            S.push_back({r,l});
            continue;
        }
        
        double a=A[i]*A[i]+B[i]*B[i];
        double b=2*A[i]*C[i];
        double c=C[i]*C[i]-B[i]*B[i]*d*d;
        if(b*b-4*a*c<0)continue;
        double x1=-b/(2*a)-sqrt(b*b-4*a*c)/(2*a);
        double y1=(-C[i]-A[i]*x1)/B[i];
        double l=atan2(y1,x1);
        double x2=-b/(2*a)+sqrt(b*b-4*a*c)/(2*a);
        double y2=(-C[i]-A[i]*x2)/B[i];
        double r=atan2(y2,x2);
        if(l>r)swap(l,r);
        v.push_back(l);
        v.push_back(r);
        S.push_back({r,l});
    }
    sort(v.begin(),v.end());
    v.erase(unique(v.begin(),v.end()),v.end());
    sort(S.begin(),S.end());
    int sum=0;
    memset(tr,0,sizeof tr);
    for(auto t:S){
        double R=t.first;
        int r=lower_bound(v.begin(),v.end(),R)-v.begin()+1;
        double L=t.second;
        int l=lower_bound(v.begin(),v.end(),L)-v.begin()+1;
        sum+=query(l);
        add(l,1);
        add(r+1,-1);
    }
    return sum;
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin>>n>>k;
    for(int i=1;i<=n;i++)cin>>A[i]>>B[i]>>C[i];
    double l=0,r=3e6;
    while(r-l>1e-6){
        double mid=(l+r)/2;
        if(check(mid)>=k)r=mid;
        else l=mid;
    }
    printf("%.6lf",r);
}

D

考虑遍历数组A，对Ai进行讨论。为了避免重复计算还要记录Ai上一次出现的位置d (边遍历边更新)。

计算区间长度R-L+1=Ai，L>d，且区间包含Ai的区间【L，R】的个数。

#include<bits/stdc++.h>
using namespace std;

int main() {
    int tc; cin >> tc;
    while (tc--) {
        int n; cin >> n;

        vector< int >a(n);
        for (int i = 0; i < n; i++)cin >> a[i];
        long long res = 0;
        map< int, int > mp;
        for (int i = 0; i < n; i++) {
            int l = a[i];
            int s = (i - l + 1 >= 0) ? i - l + 1 : 0;
            map< int, int >::iterator itr = mp.find(a[i]);
            if (itr != mp.end() and (*itr).second >= s) s = (*itr).second + 1;
            int k = (s + l - 1 >= n) ? n - 1 : s + l - 1;
            if (k - s + 1 != l)continue;
            res = res + min(i - s + 1, n - k);
            mp[a[i]] = i;
        }
        cout << res << "\n";
    }
}

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 5;
int n, T, last[N];

signed main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin >> T;
    while(T--)
    {
        cin >> n;
        memset(last, 0, sizeof last);
        int ans = 0;
        for(int i = 1; i <= n; ++i)
        {
            int x; cin >> x;
            int l = max(i - x + 1, last[x] + 1), r = min(i, n - x + 1);
            last[x] = i;
            if(l <= r) ans += r - l + 1;
        }
        cout << ans << '\n';
    } 
    return 0;
}

E

考虑dp， f [ i ] [ j ] = { a , b } f[i][j]=\{a,b\} f[i][j]={a,b}表示走到 i i i 号景点且当前出行方式为$ j$ 时所用的最短时间为 a ，最少更换次数为 b 。其中 j = 0 j=0 j=0表示骑共享单车， j = 1 j=1 j=1表示打车。

假设 i − 1 i-1 i−1号点与 i i i 号点的横坐标差值为 d x = a b s ( x i − x i − 1 ) dx=abs(x_i-x_{i-1}) dx=abs(xi​−xi−1​),纵坐标差值为 d y = a b s ( y i − y i − 1 ) dy=abs(y_i-y_{i-1}) dy=abs(yi​−yi−1​)，若不考虑换车时间，两者最短路径为 d = m i n ( d x , d y ) + a b s ( d x − d y ) d=min(dx,dy)+abs(dx-dy) d=min(dx,dy)+abs(dx−dy)。（ m i n ( d x , d y ) min(dx,dy) min(dx,dy)为斜着走的路程， a b s ( d x − d y ) abs(dx-dy) abs(dx−dy)为上下左右走的路程）

状态转移如下：

  1. 若从 i − 1 i-1 i−1 到 i i i 的过程中不换出行方式

    a. 若骑共享单车则只能往上下左右走，花费时间为 d x + d y dx+dy dx+dy，即 f [ i ] [ 0 ] = f [ i − 1 ] [ 0 ] + { d x + d y , 0 } f[i][0]=f[i-1][0]+\{dx+dy,0\} f[i][0]=f[i−1][0]+{dx+dy,0}

    b. 若打车则只能斜走，且仅当 ( d x + d y ) % 2 = = 0 (dx+dy)\%2==0 (dx+dy)%2==0时能够到达,花费时间为 d d d，即 f [ i ] [ 1 ] = f [ i − 1 ] [ 1 ] + { d , 0 } f[i][1]=f[i-1][1]+\{d,0\} f[i][1]=f[i−1][1]+{d,0}

  2. 若从 i − 1 i-1 i−1 到 i i i 的过程中换出行方式，由于两点之间最少只需要换一次出行方式即可到达，所以到 i i i号点的最短时间为到 i − 1 i-1 i−1号点的最短时间加上最短路程+1，即

    a. f [ i ] [ 0 ] = m i n ( f [ i ] [ 0 ] , f [ i − 1 ] [ 1 ] + { d + 1 , 1 } ) f[i][0]=min(f[i][0],f[i-1][1]+\{d+1,1\}) f[i][0]=min(f[i][0],f[i−1][1]+{d+1,1})

    b. f [ i ] [ 1 ] = m i n ( f [ i − 1 ] [ 1 ] , f [ i − 1 ] [ 0 ] + { d + 1 , 1 } ) f[i][1]=min(f[i-1][1],f[i-1][0]+\{d+1,1\}) f[i][1]=min(f[i−1][1],f[i−1][0]+{d+1,1})

最后取 f [ n × m ] [ 0 ] f[n \times m][0] f[n×m][0]和 f [ n × m ] [ 1 ] f[n \times m][1] f[n×m][1]的较小值即可。

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> pii;
#define x first
#define y second
pii operator + (const pii& a, const pii& b){return {a.x + b.x, a.y + b.y};}
const int N = 1010, inf = 0x3f3f3f3f;
int n, m;
pii f[N * N][2], p[N * N];

signed main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin >> n >> m;
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j)
        {
            int x; cin >> x;
            p[x] = {i, j};
        }
    for(int i = 2; i <= n * m; ++i) f[i][0] = f[i][1] = {inf, inf};
    f[1][0] = f[1][1] = {0, 0};
    for(int i = 2; i <= n * m; ++i)
    {
        int dx = abs(p[i].x - p[i - 1].x), dy = abs(p[i].y - p[i - 1].y);
        int d = min(dx, dy) + abs(dx - dy);
        f[i][0] = f[i - 1][0] + make_pair(dx + dy, 0);
        if((dx + dy) % 2 == 0) f[i][1] = f[i - 1][1] + make_pair(d, 0);
        f[i][0] = min(f[i][0], f[i - 1][1] + make_pair(d + 1, 1));
        f[i][1] = min(f[i][1], f[i - 1][0] + make_pair(d + 1, 1));
    }
    pii ans = min(f[n * m][0], f[n * m][1]);
    cout << ans.x << ' ' << ans.y;
    return 0;
}

F

思维题。首先题意可以理解为给一个数组和一个整数 k k k，要求从 [ 0 , k ] [0,k] [0,k]内选取最少数量的数字加入数组中，使得 [ 0 , k ] [0,k] [0,k]区间内的任何一个数都能通过数组中某几个数字的和来表示。

假设当前数组中的数字可以拼出从 0 0 0到 s s s的所有数字，那么在数组中加入数字 m m m，并且 m ≤ s m \leq s m≤s，就可以拼出从 0 0 0到 s + m s+m s+m的所有数字，因为区间运算 [ 0 , s ] ∪ [ 0 + m , s + m ] = [ 0 , s + m ] [0,s] \cup [0+m,s+m]=[0,s+m] [0,s]∪[0+m,s+m]=[0,s+m]，这里加了 m ≤ s m\leq s m≤s的限制的原因是，保证新区间的数字也是不间断的。

因此，我们可以从小到大遍历数组中的各个数字，然后维护一个连续区间 [ 0 , s ] [0,s] [0,s]，因为每个数字的加入，都会构成一个新的拼接区间，这里需要注意的是，如果当新加入的数字不能保证区间连续时，或者数组中所有数字遍历完，仍然不能保证区间 [ 1 , s ] [1,s] [1,s]能覆盖 [ 1 , k ] [1,k] [1,k]时怎么办，就应该往数组中加入 s s s，获得 [ 1 , s + s ] [1,s+s] [1,s+s]的连续区间， 此时++ans。

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 5;
int n, k, a[N];

signed main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin >> n >> k;
    for(int i = 0; i < n; ++i) cin >> a[i];
    sort(a, a + n);
    long long x = 1;  //这里的x是题解中的s+1，即第一个不在区间里的数
    int i = 0, ans = 0;
    while(x <= k)
    {
        if(i < n && a[i] <= x) x += a[i], ++i;
        else x <<= 1, ans++;
    }
    cout << ans;
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/348749.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Spring容器演示——采用Spring配置文件管理Bean

Spring容器演示——采用Spring配置文件管理Bean

一、创建Maven项目 创建Maven项目 - SpringDemo&#xff0c;设置项目位置以及组ID 修改项目的Maven配置 二、添加Spring依赖 在Maven仓库里查找Spring框架&#xff08;https://mvnrepository.com&#xff09; 查看Spring Core 选择版本 - 5.3.25 添加到pom.xml文件的元…
阅读更多...
盘点程序员都不一定知道的小众网站！建议收藏，java编程必备！

盘点程序员都不一定知道的小众网站！建议收藏，java编程必备！

俗话说的好&#xff0c;有一个趁手的工具解决了80%的疑虑。作为智慧物种的新新人类&#xff0c;手上掌握一两个不为人知的好用网站已经是件稀疏平常的事情。 今天我们就一起来看看&#xff0c;有哪些小众网站是程序员必备的&#xff01; 业内人士都知道&#xff0c;一直劈里啪…
阅读更多...
windows下面安装Python和pip终极教程

windows下面安装Python和pip终极教程

Python的语言风格很nice&#xff0c;但是这门语言对于windows并不算很友好&#xff0c;因为如果是初学者在windows环境下安装&#xff0c;简直是折磨人&#xff0c;会遇到各种蛋疼的情况。本文希望提供傻瓜式的教程&#xff0c;能够令读者成功安装Python和pip。 第一步&#xf…
阅读更多...
什么是push通知栏消息？

什么是push通知栏消息？

我是3y&#xff0c;一年CRUD经验用十年的markdown程序员&#x1f468;&#x1f3fb;‍&#x1f4bb;常年被誉为职业八股文选手 今天继续更新Austin&#xff0c;给Austin新增一个发送渠道&#xff08;PUSH通知栏推送&#xff09; Push通知栏消息是非常常见的&#xff0c;几乎每…
阅读更多...
【elementUI】自定义封装el-upload上传内容

【elementUI】自定义封装el-upload上传内容

文章目录为实现如图所示功能&#xff0c;点击第一步弹出模态框&#xff0c;第二部将所有文件导入&#xff0c;第三步点击确定的时候上传到后台接口&#xff0c;封装一个组件 1.搭建template <div style"display: inline-block; margin-left: 10px;"><el-bu…
阅读更多...
leaflet 设置多个marker，导出为一个geojson文件（066）

leaflet 设置多个marker，导出为一个geojson文件（066）

第066个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中使用L.marker设置多个markers， 通过数据重组，导出为geojson文件。 这里面 ayer instanceof L.Marker 是一个很重要的判断条件，可以灵活地去运用。 直接复制下面的 vue+openlayers源代码，操作2分钟即可…
阅读更多...
Ubuntu20.04LTS设置DNS解析（解决系统重启DNS不生效的问题）

Ubuntu20.04LTS设置DNS解析（解决系统重启DNS不生效的问题）

文章目录背景介绍解决方案背景介绍 近期买了一台戴尔的工作站&#xff0c;搭建的是Ubuntu20.04系统&#xff0c;使用时发现Ubuntu20.04系统上网经常卡顿&#xff08;上网方式是有线网&#xff0c;使用的千兆网口和千兆网线&#xff09;。 使用网速测试工具speedtest-cli进行了…
阅读更多...
redis五大数据结构

redis五大数据结构

目录1.1 Redis数据结构-动态字符串1.2 Redis数据结构-intset1.3 Redis数据结构-Dict1.4 Redis数据结构-ZipList1.5 Redis数据结构-ZipList的连锁更新问题1.6 Redis数据结构-QuickList1.7 Redis数据结构-SkipList1.8 Redis数据结构-RedisObject2.0 Redis数据结构-String2.1 Redi…
阅读更多...
前端性能优化的整理笔记

前端性能优化的整理笔记

&#x1f6b4; 前言大厂面试题分享 面试题库后端面试题库 &#xff08;面试必备&#xff09; 推荐&#xff1a;★★★★★地址&#xff1a;前端面试题库&#x1f3c4;利用碎片化的时间&#xff0c;系统的整理&#xff0c;性能优化的知识点。&#x1f3af; 前端性能优化&#xf…
阅读更多...
初识网络原理，关于网络编程的基础

初识网络原理，关于网络编程的基础

一.网络的重要性对于程序员而言&#xff0c;几乎所程序都依赖于网络&#xff0c;对于公司来说&#xff0c;几乎所有产品也是依赖于网络&#xff0c;这些产品不仅包括面向用户的产品&#xff0c;公司内部的一些服务也是基于公司内网来进行相互调用的。二.组网方式①基于网线直连…
阅读更多...
每日学术速递2.15

每日学术速递2.15

CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.YOWOv2: A Stronger yet Efficient Multi-level Detection Framework for Real-time Spatio-temporal Action Detection 标题&#xff1a;YOWOv2&#xff1a;用于实时时空动作检测的…
阅读更多...
Jenkins构建项目和tomcat项目发布脚编写本详细教程jenkins 2.361版本

Jenkins构建项目和tomcat项目发布脚编写本详细教程jenkins 2.361版本

jenkins部署教程可查看上一篇文档jenkins部署指定任意版本和配置详细教程 jenkins 2.361版本示例_争取不加班&#xff01;的博客-CSDN博客Jenkins服务器去拉取代码&#xff0c;所以要下载git客户端 yum -y install git jenkins服务器下载下面就是构建发布任务测试可以性测试使用…
阅读更多...
第一个Python程序-HelloWorld与Python解释器

第一个Python程序-HelloWorld与Python解释器

数据来源 01 第一个Python程序-HelloWorld 1&#xff09;打开cmd&#xff1a; windows R 打开运行窗口输入cmd 2&#xff09;进入Python编写页面 输入&#xff1a;python 3&#xff09;然后输入要写的Python代码然后回车 print("Hello World!!!") print() …
阅读更多...
利用AxhubCharts元件库在Axure RP中快速创建可视化统计图

利用AxhubCharts元件库在Axure RP中快速创建可视化统计图

利用AxhubCharts元件库在Axure RP中快速创建可视化统计图&#xff0c;可创建的可视化统计图有折线图、柱状图、堆叠柱状图、条形图、堆叠条形图、面积图、饼图、环形图、漏斗图、甘特图、散点图等。具体操作步骤见下文。 1.下载AxhubCharts.rplib元件库文件 2.载入AxhubChart…
阅读更多...
【Node.js】模块化

【Node.js】模块化

模块化模块化的基本概念模块化规范Node.js中模块化分类模块作用域向外共享模块作用域的成员Node.js中的模块化规范模块化的基本概念 指解决一个复杂问题时&#xff0c;自顶向下逐层把系统划分成若干模块的过程对于整个系统来说&#xff0c;模块是可组合&#xff0c;分解和更换…
阅读更多...
mysql的一些底层学习

mysql的一些底层学习

数据库三大范式 1、第一范式&#xff1a;确保每列保持原子性 2、第二范式&#xff1a;确保表中每列都与主键列相关 3、第三范式&#xff1a;确保表中每列都与主键列直接相关而不是间接相关 不要一味的去追求符合范式要求&#xff0c;实际项目中&#xff0c;需求 > 性能 …
阅读更多...
GPT-3(Language Models are Few-shot Learners)简介

GPT-3(Language Models are Few-shot Learners)简介

GPT-3(Language Models are Few-shot Learners) GPT-2 网络架构 GPT系列的网络架构是Transformer的Decoder&#xff0c;有关Transformer的Decoder的内容可以看我之前的文章。 简单来说&#xff0c;就是利用Masked multi-head attention来提取文本信息&#xff0c;之后利用MLP和…
阅读更多...
内嵌于球体的多边形

内嵌于球体的多边形

( A, B )---2*30*2---( 1, 0 )( 0, 1 ) 做一个网络让输入只有2个节点&#xff0c;每个训练集里有两张图片&#xff0c;让B的训练集全为0&#xff0c;排列组合A&#xff0c;观察迭代次数平均值的变化。 共得到32组数据&#xff0c; 差值结构 A-B 迭代次数 1 1 3*2*0*0 104…
阅读更多...
计算机网络学习笔记（二）物理层

计算机网络学习笔记（二）物理层

物理层&#xff08;传输比特0/1&#xff09;基本概念 物理层下的传输媒体 1. 导引型 同轴电缆&#xff0c;双绞线&#xff08;绞合可抵御干扰&#xff09;&#xff0c;光纤&#xff0c;电力线 2. 非导引型&#xff08;调制振幅 频率 相位&#xff09; 无线电波&#xff0c;微…
阅读更多...
SpringBoot整合MybatisPlus（powernode CD2207）（内含教学视频+源代码）

SpringBoot整合MybatisPlus（powernode CD2207）（内含教学视频+源代码）

SpringBoot整合MybatisPlus&#xff08;powernode CD2207&#xff09;&#xff08;内含教学视频源代码&#xff09; 教学视频源代码下载链接地址&#xff1a;https://mp.csdn.net/mp_download/manage/download/UpDetailed 目录SpringBoot整合MybatisPlus&#xff08;powernode…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023