Approximation Schemes(近似方案)

PTAS（Polynomial time approximation scheme）

定义：

若对于每一个固定的 $ϵ>0$ ，算法 A 的运行时间以实例 $I$的规模的多项式为上界，则称 A 是一个多项时间近似方案。

FPTAS（Fully polynomial time approximation scheme）

定义：

在 PTAS 的基础上，进一步要求算法 A 的运行时间以实例 $I$的规模和 $1/ϵ$ 的多项式为上界，则称 A 是一个完全多项时间近似方案。FPTAS 被认为是最值得研究的近似算法，仅有极少数的 NP-hard 问题存在 FPTAS。

PPTAS（Pseudo-polynomial time approximation scheme）

定义：

如果算法的时间复杂度可以表示为输入数值规模 N 的多项式，但是运行时间与输入值规模 N 的二进制位数呈指数增长关系，则称其时间复杂度为伪多项式时间。一个具有伪多项式时间复杂度的NP完全问题称之为弱NP完全问题，而在 P!=NP 的情况下，若一个NP完全问题被证明没有伪多项式时间复杂度的解，则称之为强NP完全问题。

伪多项式时间 0-1背包问题

• 如果数值算法的运行时间是输入数值的多项式，但不一定是输入长度的多项式（表示它所需的位数），则该算法在伪多项式时间内运行
• 0-1背包问题的动态规划算法的运行时间为$O(W\ast n)$，$W$需要$\log W$位来描述，因此它是伪多项式。
• 其他伪多项式算法：原始性测试

问题描述

• 设P为最大利润，即$P=ma{x}_{a\in S}P(a)$。由此，对于$n$个对象，我们最多获取$nP$的利润上限。在这里，我们可以假设每一项的好处都是内在价值。
• 对于每个 i ∈ { 1 ， … ， n } i∈\{1，…，n\} i∈{1，…，n}和 p ∈ { 1 ， … … ， n P } p∈\{1，……，nP\} p∈{1，……，nP}，设$S_{i,p}$表示总利润恰好为$p$的 { a 1 ， … ， a i } \{a_1，…，a_i\} {a1​，…，ai​}的子集，并且占用尽可能少的空间
• 设$A(i，p)$是集合$S_{i,p}$的大小，其值为$\infty$，表示没有这样的子集。
• 对于$A(i，p)$，我们有基本情况$A(1，p)$其中$A(1,p(a_1))$是$s(a1)$，所有其他值都是$\infty$。

近似算法解法

递归式：

• 然后，最优子集对应于集合$S_{n,p}$，其中$p$最大且$A(n,p)\le B$。由于这最多迭代$n$个不同的值来计算每个$A(i,p)$，我们得到了$O(n^{2}P)$的总运行时间，因此得到了背包的伪多项式算法
• 很容易修改上述DP算法以实现0-1背包的全多项式时间逼近方案（FPTAS）
• $DPFORKNAPSACK()$
  1：Let P be the maximum benefit of all items
  2：Given $\epsilon >0$，let $K=\epsilon \cdot P/n$。
  3：for each object $a_i$ do
  4：define a new profit $p^{\prime }(a_i)=\lfloor \frac{p(a_i)}{K}\rfloor$。
  5：将这些$p^{\prime }(a_i)$作为n个项目的利润，使用动态规划算法，找到最大利润的集合$S^{\prime }$。
  6：输出$S^{\prime }$作为原始背包问题的最终解
• 定理：由上述算法输出的集合S′满足：
  • $$P(S^{\prime })\ge (1-\epsilon )\cdot OPT$$。这里$P(S^{\prime })$表示集合$S^{\prime }$的利润（或收益），OPT是原始问题的最佳收益

证明

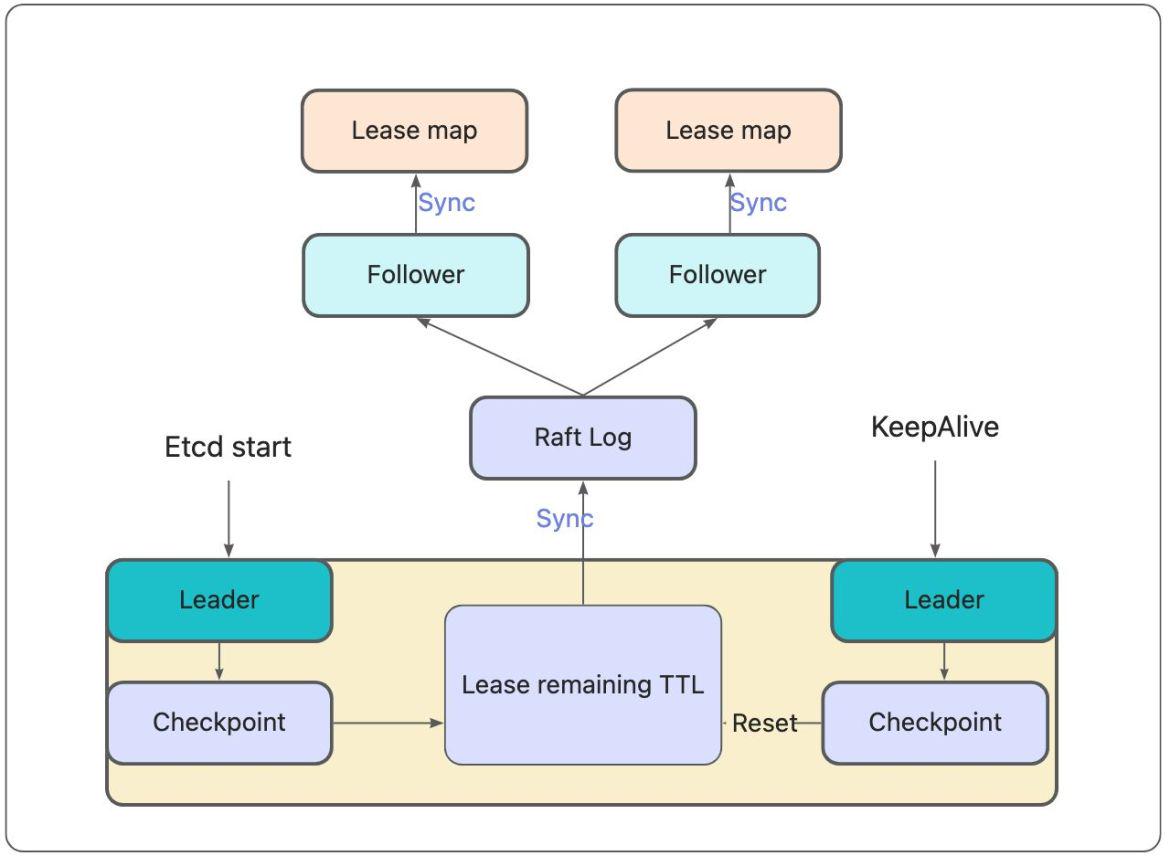
0-1背包问题近似算法