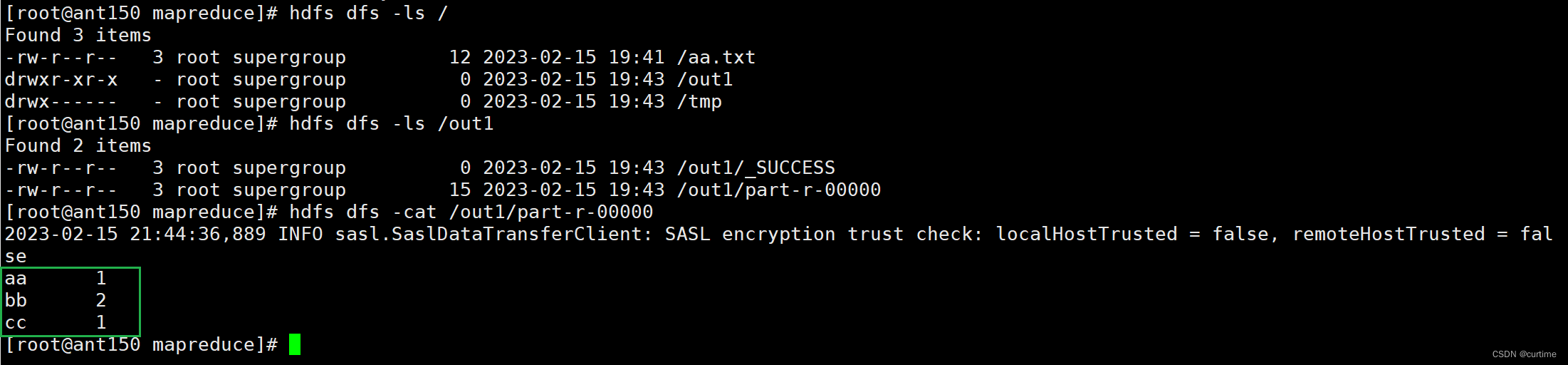
复习提纲

 

题型：编程题3题，综合题4题。

一、编程题：

1、链表的类型定义；邻接矩阵表示图的类型定义；链接表表示图的类型定义；vector数组表示图的定义和使用方法。

2、链表中结点的插入和删除操作，时间复杂度分析。

3、图的连通分量的计算方法：DFS、BFS和并查集。

4、基于有序序列进行二分查找的实现原理和实现方法，时间复杂度分析。

二、综合题

包括画图、计算和算法描述等方面。

1、广义表的结构图以及广义表的表头、表尾、表长和深度。

2、哈夫曼树的构建步骤、构建过程以及带权路径长的计算方法。

3、最小生成树(Kruskal算法、Prim算法)的一般步骤。有一个图生成最小生成树的过程。

4、二叉查找树中插入和删除一个键值的一般步骤、由一个键值序列生成一棵二叉查找树的过程、在一棵二叉查找树中删除一个键值的过程。

注意：考试试题都来自与教材的习题，但是部分题目的数据和要求会做适当的调整。

链表知识全：(1条消息) 链表详解来啦_努力的小羽儿的博客-CSDN博客_链表详解

一、编程题：

1、链表的类型定义；

typedef struct clNode {
	datatype data; //数据域
	clNode* next; //链域
	clNode() :next(NULL) {
		data = 0;
	}
}*chainList;

邻接矩阵表示图的类型定义；

struct adjMatrix {
	datatype data[eNum]; //顶点的数据信息
	int edge[eNum][eNum];//邻接矩阵
	int v; //顶点的数量
	int e; //边的数量
};

链接表表示图的类型定义；

struct vertex {
	int u; //邻接点的编号
	int w; //权重，无权图可忽视该属性
	vertex* next;
	vertex(int u1=0,int w1=0):u(u1),w(w1),next(NULL){}
};
 
typedef struct llNode {
	datatype data[vNum]; //顶点的数据信息
	vertex* edges[vNum]; //边表
	int v, e; //顶点数和边数
	llNode() :v(0), e(0) {
		for (int i = 0; i < vNum; i++)
			edges[i] = NULL;
	}
}*linkList;

vector数组表示图的定义和使用方法。

//图的vector数组表示的类型定义
struct edge {
	int v; //邻接点
	int w; //权重，无权图可忽视该属性
	edge(int v1, int w1) :v(v1), w(w1) {};
};

typedef struct vgNode {
	vector<edge>edges[vNum]; //边表
	datatype data[vNum]; //顶点的数据信息
	int v, e; //顶点数和边数
}vecGraph;
 
//创建vector数组表示的图
void create_vecGraph(vecGraph& g) {
	int i, u, v, w;
	cin >> g.v >> g.e; //输入顶点数和边数
	for (i = 0; i < g.e; i++) {
		cin >> u >> v >> w; //输入边的信息，无权图省略w，且下列语句w变为1
		g.edges[u].push_back(edge(v, w)); //将边（u，v）加入图中
		g.edges[v].push_back(edge(u, w)); //将边（v,u）加入图中，有向图忽略该语句
	}
}
 
//在实际应用中，可以采取如下更简单的表示方法
int v; //顶点数
vector<int>g[vNum]; //无权图
vector<pair<int, int>>g1[vNum]; //有权图，pair中的first代表邻接点，second代表权重

2、链表中结点的插入和删除操作，时间复杂度分析。

void cl_insert(chainList p, datatype x)
{
	chainList q = new clNode;//定义新的结点，用指针指向新定义的指针
	//判断是否有足够的空闲存储空间存放新结点
	if (q == NULL)
	{
		cout << "插入结点失败！" << endl;
		return;
	}
	q->data = x;
	q->next = p->next;
	p->next = q;
}

//查询循环链表中是否存在值为x的结点
chainList rcl_search(chainList h, datatype x)
{
	if (h == NULL) return NULL;
	chainList h1 = h;
	do {
		h1 = h1->next;
		if (h1->data == x)return h1;
	} while (h1 != h);
	return NULL;
}

void cl_delete(chainList h, datatype x)
{
	chainList p = new clNode;
	p = cl_search(h, x);
	if (p == NULL)return;
	chainList q = p->next;
	if (q == NULL)return;
	p->next = q->next;
	delete q; //释放了q所占用的空间，但q指针仍有指向
	q = NULL; //设置为空指针
}

3、图的连通分量的计算方法：DFS、BFS和并查集。

DFS：

#include<iostream>
#include<vector>
using namespace std;
constexpr auto eNum = 102; //图的顶点数量
constexpr auto vNum = 200; //图的边的数量
typedef string dataType; //图顶点中存放数据信息的类型
typedef int datatype;
constexpr auto INF = 0x3f3f3f3f;
 
//图的深度优先搜索，以下模板基于vector数组所表示的图（有向图/无向图）
bool vis[vNum]; //标记每一个顶点的颜色
int dfn[vNum], cnt = 0; //dfn存放DFS序列，cnt为序列的编号
//对图g的顶点cur所在的连通分量进行深度优先搜索，初始出发顶点为cur
void dfs(vector<datatype>g[vNum], int cur) {
	int i, u;
	dfn[++cnt] = cur; //将当前顶点cur的深度优先编号为cnt
	vis[cur] = true; //将当前顶点涂为黑色
	for (i = 0; i < g[cur].size(); i++) { //检查cur的每一个邻接点
		u = g[cur][i]; 
		if (!vis[u]) //u为白色，（cur,u）为树边
			dfs(g, u); //从u出发继续搜索
	}
}
 
//对图g进行深度优先搜索，v为顶点的数量
void dfs_traverse(vector<int>g[vNum], int v) {
	int i;
	memset(vis, 0, sizeof(vis)); //将每个顶点都设置为白色
	for (i = 1; i <= v; i++)
		if (!vis[i]) //如果存在白色顶点，则从该顶点出发进行深度优先搜索
			dfs(g, i);
}
 
int main() {
 
}

BFS：

#include<iostream>
#include<vector>
#include<queue>
using namespace std;
constexpr auto eNum = 102; //图的顶点数量
constexpr auto vNum = 200; //图的边的数量
typedef string dataType; //图顶点中存放数据信息的类型
typedef int datatype;
constexpr auto INF = 0x3f3f3f3f;
 
bool vis[vNum]; //标记顶点的颜色
int bfn[vNum]; //广度优先序列
//对图g中cur所在的连通分量进行广度优先搜索，初始出发点为cur
void bfs(vector<int>g[vNum], int cur) {
	int i, u, v, cnt = 0;
	queue<int>q;
	bfn[++cnt] = cur, vis[cur] = true;
	q.push(cur); //将初始出发点加入队列
	while (!q.empty()) { //对队列中的元素进行处理，直到队空
		u = q.front(), q.pop(); //取出队头元素
		for (i = 0; i < g[u].size(); i++) { //检查顶点u的每一个邻接点
			v = g[u][i];
			if (!vis[v]) { //顶点v为白色
				//（u，v)为树边
				bfn[++cnt] = v;
				vis[v] = true;  //加入队列前将v设置为黑色
				q.push(v); //将v加入队列
			}
 
		}
	}
}
 
//对图g进行广度优先搜索，v为顶点的数量
void bfs_traverse(vector<datatype>g[vNum], int v) {
	memset(vis, 0, sizeof(vis));//将每个顶点设置为白色
	for (int i = 1; i <= v; i++)
		if (!vis[i]) //如果顶点i为白色，则从i出发对其所在的连通分量进行bfs
			bfs(g, i);
}
 
int main() {
 
}

 并查集：

#include<iostream>
using namespace std;
typedef int datatype;
constexpr auto N = 100;
//由并查集的两种操作可知，并查集的操作中主要涉及结点的父节点和树的根结点，
//因此可以采用树的双亲表示法表示并查集。
//由下面并查集的类型定义可知，初始并查集每个集合里就一个元素，mq即表示一个并查集。
struct mqNode {
	int pa;
	datatype data;
	mqNode() :pa(-1) {};
}mq[N];
 
//并查集的查询操作
int query(int x) {
	if (mq[x].pa == -1)return x; //x没有父节点，则x为根结点
	mq[x].pa = query(mq[x].pa); //向上查询x的父节点，并进行路径压缩，让x到根结点的路径都独立出来，成为第二层节点，链接根结点
	return mq[x].pa;
}
 
//并查集的合并操作：1.获取两个元素所在树的根结点 2.检查两个元素是否属于同一集合
void merge(int x, int y) {
	x = query(x), y = query(y);
	if (x != y)
		mq[x].pa = y;
}
 
int main() {
 
}

4、基于有序序列进行二分查找的实现原理和实现方法，时间复杂度分析。

实现原理：

将位于顺序表中间元素的键值与查找键值比较，如果两者相等，则查找成功；否则以中间元素为分割点，将顺序表分割为两个子表，然后在某个子表中进行同样的操作。重复上述过程，直到查找到相应的元素或子表为空。

实现原理：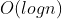 

int binary_search(vector<int>sl, int k) {
	int left = 0, right = sl.size() - 1, mid;
	while (left <= right) {
		mid = (left + right) >> 1;
		if (sl[mid] == k) return mid;
		else if (sl[mid] > k) right = mid - 1;
		else left = mid + 1;
	}
	return -1;
}

二、综合题

包括画图、计算和算法描述等方面。

1、广义表的结构图以及广义表的表头、表尾、表长和深度。

结构图

 

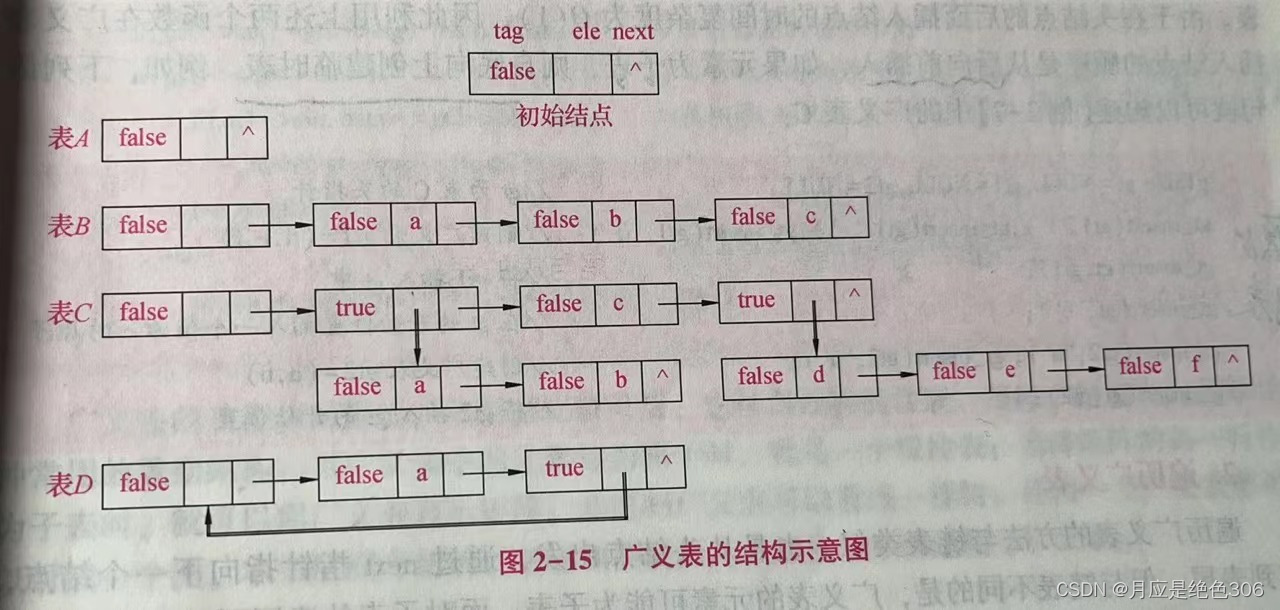
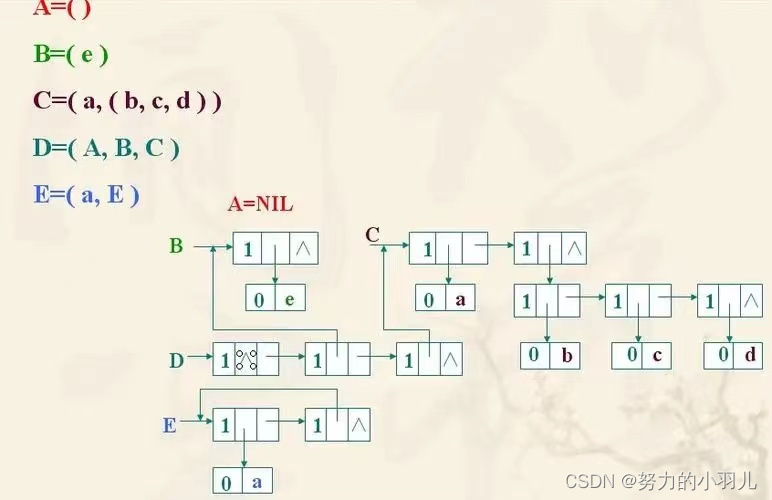
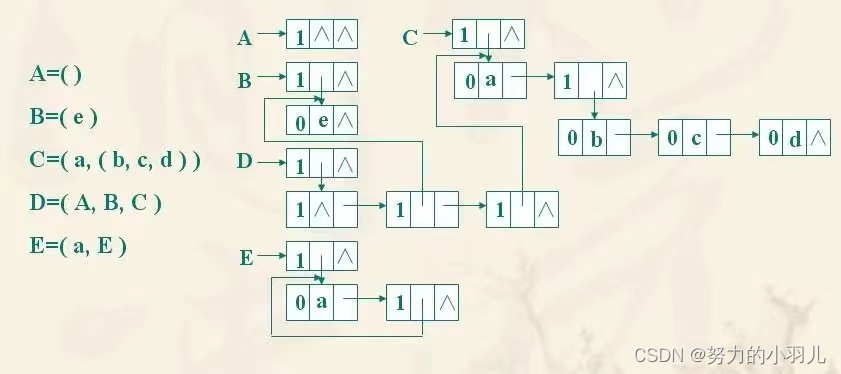
广义表是由n个元素组成的序列：LS = （a1，a2, ... an）;其中 ai是一个原子项或者是一个广义表。n是广义表的长度。若ai是广义表，则称为LS的子表。

广义表表头和表尾： 若广义表LS不空，则a1，称为LS的表头，其余元素组成的子表称为表尾。

广义表的长度： 若广义表不空，则广义表所包含的元素的个数，叫广义表的长度。

广义表的深度： 广义表中括号的最大层数叫广义表的深度。 

广义表的广度（长度）指：广义表中所包含的数据元素的个数。例：

在广义表{a，{b，c，d}}中，它包含一个原子和一个子表，因此该广义表的长度为2.

在广义表{{a，b，c}}中只有一个子表{a，b，c}，因此它的长度为1.

例如：
对广义表LS=((),a,b,(a,b,c),(a,(a,b),c))
表头为子表LSH = ();
表尾为子表LST = (a,b,(a,b,c),(a,(a,b),c));
广义表LS的长度：5
广义表LS的深度：3

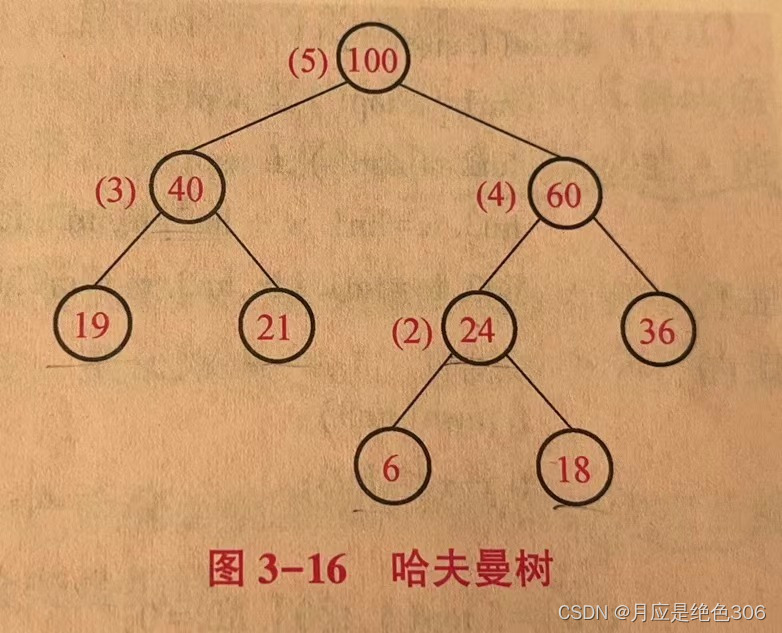
2、哈夫曼树的构建步骤、构建过程以及带权路径长的计算方法。

算法步骤

（1）初始化 ：构造m棵只有一个结点的二叉树，得到一个二叉树集合F={T1,T2...}，Ti的叶结点（也是根结点）的权重为Wi；

（2）选取与合并：新建一个结点tmp，在F中选取根结点权重最小和次小的两棵二叉树Ti和Tj，分别作为tmp的左子树和右子树(顺序可以颠倒），构造一棵二叉树，结点tmp的权重为Ti和Tj的权重之和

（3）删除与加入：在F中删除Ti和Tj，并将以 tmp为根结点的新建二叉树加入F中；

（4）重复步骤(2)和步骤(3)，直到F中只剩下一棵二叉树为止，此时，这棵二叉树就是哈夫曼树。           
 

 

#include<iostream>
#include<queue>
using namespace std;
typedef char datatype;
constexpr auto M = 30;;
//由于结点的总数不是太大，因此可以用二叉树左右链数组的表示法做适当的扩展来表示哈夫曼树的特点
//结点定义
typedef struct hutNode {
	datatype data;
	int w, idx; //idx为结点的下标，w表示权重
	int lc, rc;
	bool operator<(const hutNode& hn)const {
		return w > hn.w; //为了使hutNode类型的优先队列中权重较小的优先级较高
	}
}huTree[M<<1];
 
//由于每一步都要选择集合F中的最小权重结点和次小权重结点，
//且F中的结点是不断更新的，因此可以使用priority_queue
//创建哈夫曼树t：参数m为叶结点的数量，data和w分别为叶结点的数据信息和叶结点的权重
void huTree_create(huTree& t, const datatype data[], int w[], int m) {
	int i;
	hutNode hn1, hn2, hn3;
	priority_queue<hutNode>f;
	for (i = 1; i <= m; i++) {
		t[i].data = data[i - 1], t[i].w = w[i - 1], t[i].idx = i;
		t[i].lc = -1, t[i].rc = -1;
		f.push(t[i]);
	}
		while (f.size() > 1) { //当f只剩下一个元素时结束循环
			hn1 = f.top(), f.pop();
			hn2 = f.top(), f.pop();
			hn3.w = hn1.w + hn2.w, hn3.idx = i;
			hn3.lc = hn1.idx, hn3.rc = hn2.idx;
 
			f.push(hn3);
			t[i++] = hn3;
		}
		t[0] = f.top(), t[0].idx = 0; //将最终哈夫曼树的根结点的编号设置为0	
}
 
int main() {
	const char* data = "EDCBA";
	int w[] = { 6,18,21,36,19 };
	huTree t;
	huTree_create(t, data, w, 5);
}

3、最小生成树(Kruskal算法、Prim算法)的一般步骤。有一个图生成最小生成树的过程。

Kruskal算法：

 

一般步骤

（1）定义点集U，并定义一个集合D，编号为v的顶点对应D[v]，D[v]包括两个属性：属性d表示v到U的距离，初始时d的值为INF；属性to属于U，且边（v,to）的权重为v到U的最短距离。初始时选择任一顶点v加入U，更新v的邻接点的D的值；

（2）利用D的属性d在V-U中选择到U的距离最小的值顶点v并加入U中，另D[v]=INF，同时江边（v,D[v]，to）加入最小生成树中；

（3）利用v更新D，当v的某个邻接点在V-U中时，设边（v,u）的权重为w，如果w<D[u].d，则令D[u].d=w，D[u].to=v；

（4）重复步骤（2）（3），知道所有顶点都加入U中为止。

简言之，就是从第一个顶点开始，然后寻找临近的点，点的信息放入小顶堆中（以距离排序），然后进入while循环，循环n-1次；取出小顶堆的top，即最小的距离，固定住，将该顶点加入u，树边也固定住，然后遍历该顶点的连接点，重复上述操作。

Prim算法：

判断两个顶点是否属于同一颗子树，可用并查集。 

4、二叉查找树中插入和删除一个键值的一般步骤、由一个键值序列生成一棵二叉查找树的过程、在一棵二叉查找树中删除一个键值的过程。