我们需要解决的问题:
1: 什么是bp 神经网络?
2:理解bp神经网络需要哪些数学知识?
3:梯度下降的原理
4: 激活函数
5:bp的推导。
1.什么是bp网络?
引用百度知道回复:
“我们最常用的神经网络就是BP网络,也叫多层前馈网络。BP是back propagation的所写,是反向传播的意思。我以前比较糊涂,因为一直不理解为啥一会叫前馈网络,一会叫BP(反向传播)网络,不是矛盾吗?其实是这样的,前馈是从网络结构上来说的,是前一层神经元单向馈入后一层神经元,而后面的神经元没有反馈到之前的神经元;而BP网络是从网络的训练方法上来说的,是指该网络的训练算法是反向传播算法,即神经元的链接权重的训练是从最后一层(输出层)开始,然后反向依次更新前一层的链接权重。因此二者并不矛盾,只是我没有理解其精髓而已”
随便提一下BP网络的强大威力:
1)任何的布尔函数都可以由两层单元的网络准确表示,但是所需的隐藏层神经元的数量随网络输入数量呈指数级增长;
2)任意连续函数都可由一个两层的网络以任意精度逼近。这里的两层网络是指隐藏层使用sigmoid单元、输出层使用非阈值的线性单元;
3)任意函数都可由一个三层的网络以任意精度逼近。其两层隐藏层使用sigmoid单元、输出层使用非阈值的线性单元。
2:理解bp神经网络需要哪些数学知识?
需要知道什么是导数,什么是偏导? 什么是链式推导?
导数:
导数的求法示范: f(x)=2x 的导数是 2
f(x)=x*x 的导数是 2x
f(x)=x*x*x +3*x+4 的导数是 3(x*x)+3
导数的具体的定义入门 及推导过程 通俗易懂的导数基础讲义_百度文库
偏导:
偏导的定义:也即是原来只有一个参数的f(x) 成为了多个参数 例如f(x,y)
求对x的偏导时 将y当常数
求y的偏导时 将x当常数。
推导示范:
f(x,y)=2x*x + 3y+4
对x的导数: 4x (没有x的常数项为0)
对y的导数: 3
看下偏导入门 偏导数的定义及其计算法_图文_百度文库
链式推导:
示范:
f(g(x))=(g(x))*(g(x))
g(x)=3x
则f(g(x))对x的导数为=f(g(x))的导数 * 个g(x)的导数
= (2*(g(x)))*3
= 6*(g(x))
= 18x
以上 即是需要理解的数学基础。
3:梯度下降的原理
梯度下降是什么呢? 当我们用神经网络算出一个实际输出O。 这个值和期望输出d的差值 即是损失函数(就是一个和你想要的结果差距有多大)
因为在数学中不好算负值 , 所以我们把差值平方, 同时为了求导方便 对这个平方差值 乘以1/2
所以最后的损失函数就成了:
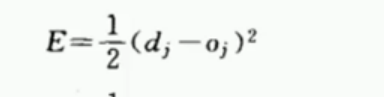
这个函数的曲线是:

以上 就是损失函数: 我们知道,这个函数,当他的导数为0的时候, 它的值最小。 所以我们在每次求出损失函数时,去求导 根据这个导数去改变权重,从而努力使这个导数接近零。
跑下 最后的代码调试下,或者去百度搜索下
4:激活函数
本文不讨论激活函数的具体原理,以后会专门介绍。 只需要知道,加入激活函数是用来 加 入非线性因素的,解决线性模型所不能解决的问题。
推荐阅读 形象的解释神经网络激活函数的作用是什么?
5:bp的推导
本次推导是对 通俗理解神经网络BP传播算法的笔记, 但是原文写的有些错误和一些地方没有说明 导致 萌新不易理解。本文会将出现的问题补齐:
主要问题有:
1: 链式推导写的太混乱 。以下是手推过程:下面的

2:求出来了代价函数对权值的偏导后 没有说明怎么应用
代价函数改变公式在下面:

在这本文 比例系数 为1 。多看几遍这个 才能理解最后代码里的权值改变:
最后 是它的 代码:
importnumpyasnpdefnonlin(x,deriv=False):
if(deriv==True):
returnx*(1-x)#如果deriv为true,求导数
return1/(1+np.exp(-x))X=np.array([[0.35],[0.9]])#输入层y=np.array([[0.5]])#输出值np.random.seed(1)W0=np.array([[0.1,0.8],[0.4,0.6]])W1=np.array([[0.3,0.9]])print'original ',W0,'\n',W1forjinxrange(100):
l0=X#相当于文章中x0
l1=nonlin(np.dot(W0,l0))#相当于文章中y1
l2=nonlin(np.dot(W1,l1))#相当于文章中y2
l2_error=y-l2
Error=1/2.0*(y-l2)**2
print"Error:",Error
l2_delta=l2_error*nonlin(l2,deriv=True)#this will backpack
#print 'l2_delta=',l2_delta
l1_error=l2_delta*W1;#反向传播
l1_delta=l1_error*nonlin(l1,deriv=True)
W1+=l2_delta*l1.T;#修改权值
W0+=l0.T.dot(l1_delta)
printW0,'\n',W1