【路径规划】基于Dijkstra算法及Floyd算法的通信与网络路径规划（Matlab代码实现）

news2024/11/25 0:42:37

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

Dijkstra算法是解决**单源最短路径**问题的**贪心算法**，它先求出长度最短的一条路径，再参照该最短路径求出长度次短的一条路径，直到求出从源点到其他各个顶点的最短路径。

基本思想：

首先假定源点为u，顶点集合V被划分为两部分：集合 S 和 V-S。初始时S中仅含有源点u，其中S中的顶点到源点的最短路径已经确定。
集合S 和V-S中所包含的顶点到源点的最短路径的长度待定，称从源点出发只经过S中的点到达V-S中的点的路径为特殊路径，
并用dist[]记录当前每个顶点对应的最短特殊路径长度。
Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

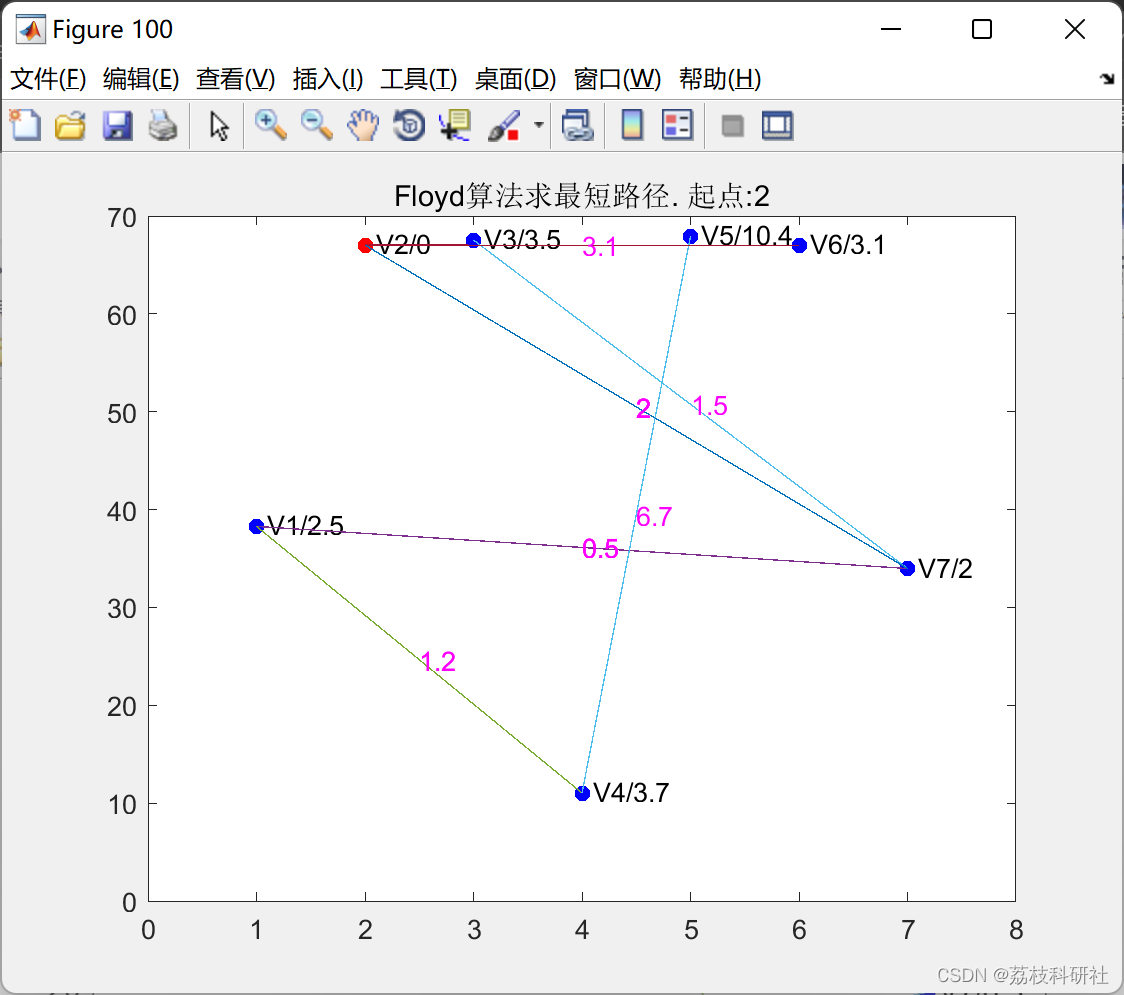
📚2 运行结果

。。。。。。

部分代码：

%标出顶点（蓝色）
for i=1:n
%text(i+0.1,point(2,i),['V',num2str(i)],'Color','b');
%hold on;
plot(i,point(2,i),'.','Color','b','MarkerSize',20);
hold on;
end
%标出起点（红色）
%text(v+0.1,point(2,v),['V',num2str(v)],'Color','r');
plot(v,point(2,v),'.','Color','r','MarkerSize',20);

%连线
for i=1:n
L=1;
while(fullPath(i,L)~=0 && fullPath(i,L+1)~=0 && dist(i)~= inf)
%路径前后两点的X坐标
X_vector=[point(1,fullPath(i,L)),point(1,fullPath(i,L+1))];
%路径前后两点的Y坐标
Y_vector=[point(2,fullPath(i,L)),point(2,fullPath(i,L+1))];
%绘制路线
plot(X_vector,Y_vector);
hold on;
%标出路线对应的长度（不标自己到自己的）
if fullPath(i,L) ~= fullPath(i,L+1)
text(mean(X_vector),mean(Y_vector),num2str(netGraph(fullPath(i,L),fullPath(i,L+1))),'Color','m')
end
hold on;
L=L+1;
end
%标出距离
text(point(1,i)+0.1,point(2,i)+0.2,['V',num2str(i),'/',num2str(dist(i))]);
axis([0,n+1,0,10*n]);
hold on;
end