表现良好的最长时间段

难度：中等

给你一份工作时间表 hours，上面记录着某一位员工每天的工作小时数。

我们认为当员工一天中的工作小时数大于 8 小时的时候，那么这一天就是「劳累的一天」。

所谓「表现良好的时间段」，意味在这段时间内，「劳累的天数」是严格 大于「不劳累的天数」。

请你返回「表现良好时间段」的最大长度。

示例 1：

输入：hours = [9,9,6,0,6,6,9]
输出：3
解释：最长的表现良好时间段是 [9,9,6]。

示例 2：

输入：hours = [6,6,6]
输出：0

前置知识：前缀和

对于数组 $\text{nums}$，定义它的前缀和 $\text{s}[0]=0$，$\text{s}[i+1]=\sum _{j=0}^i\text{nums}[j]。$
例如 $\text{nums}=[1,2,-1,2]$，对应的前缀和数组为 $s=[0,1,3,2,4]$。

通过前缀和，我们可以把子数组的元素和转换成两个前缀和的差，即

$$\sum _{j=\text{left}}^{\text{right}}\text{nums}[j]=\sum _{j=0}^{\text{right}}\text{nums}[j]-\sum _{j=0}^{\text{left}-1}\text{nums}[j]=\text{s}[\text{right}+1]-\text{s}[\text{left}]$$
例如 $\text{nums}$的子数组 $[2,-1,2]$ 的和就可以用 $s[4]-s[1]=4-1=3$ 算出来。

注：为方便计算，常用左闭右开区间 $[\text{left},\text{right})$ 来表示子数组，此时子数组的和为 $\text{s}[\text{right}]-\text{s}[\text{left}]$，子数组的长度为 $\text{right}-\text{left}$。

方法一：单调栈

思路：

先把问题转换到我们熟悉的东西上。

「劳累天数大于不劳累天数」等价于「劳累天数减去不劳累天数大于 $0$」。

那么把劳累的一天视作 $\text{nums}[i]=1$，不劳累的一天视作 $\text{nums}[i]=-1$，则问题变为：

计算 $\text{nums}$ 的最长子数组，其元素和大于 $0$。

既然说到了「子数组的元素和」，那么利用前缀和 $s$，将问题变为：

找到两个下标 $i$ 和 $j$，满足 $j<i$ 且 $s[j]<s[i]$，最大化 $i-j$ 的值。

想一想，哪些值可以作为 $j$（最长子数组的左端点）呢？

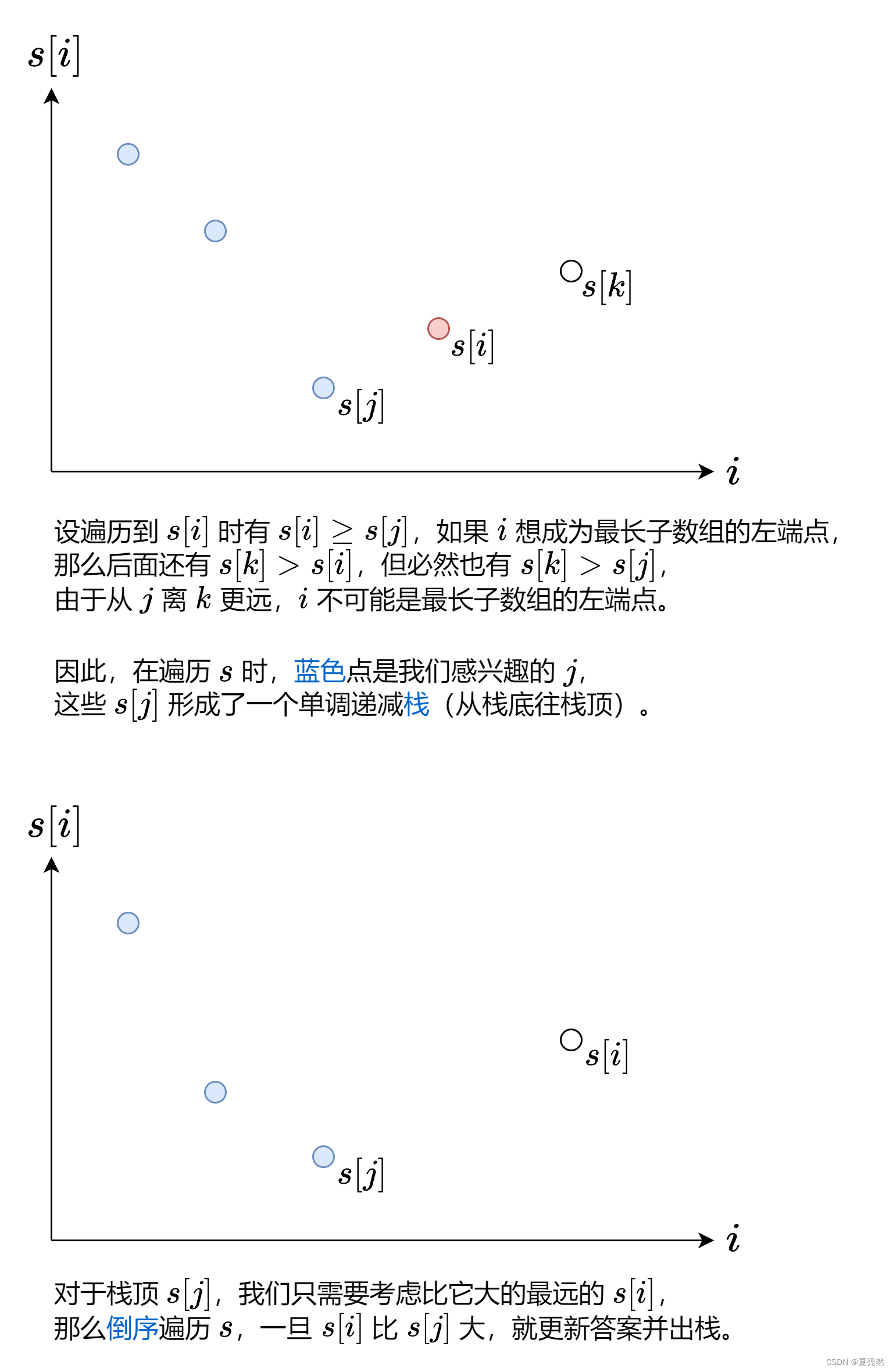
复杂度分析：

• 时间复杂度： $O(n)$，其中 $n$ 为 $\text{hours}$的长度。注意每个元素至多入栈出栈各一次，因此二重循环的时间复杂度是 $O(n)$ 的。
• 空间复杂度： $O(n)$。

class Solution:
    def longestWPI(self, hours: List[int]) -> int:
        hours_sum, start = [0] * (len(hours) + 1), [0]
        for i in range(len(hours)):
            # 前缀和
            hours_sum[i+1] = hours_sum[i] + 1 if hours[i] > 8 else hours_sum[i] - 1
            # 可能是开头的位置
            if hours_sum[start[-1]] > hours_sum[i+1]:
                start.append(i+1)
        res = 0
        for i in range(len(hours), 0, -1):
            while start and hours_sum[i] > hours_sum[start[-1]]:
                res = max(res, i - start.pop())
        return res

方法二：利用前缀和的连续性

虽说方法一更加通用，不过利用 $\text{nums}$中只有 $1$ 和 $-1$ 的特点，可以做到一次遍历。

考虑 $s[i]$：

• 如果 $s[i]>0$，那么 $j=0$ 就是最远的左端点，因为 $s[0]=0$，故 $s[i]-s[0]=s[i]>0$，符合要求。
• 如果 $s[i]\le 0$，那么 jjj 就是 $s[i]-1$ 首次出现的位置。为什么是 $s[i]-1$ 而不是其它更小的数？这是因为前缀和是从 $0$ 开始的，由于 $\text{nums}$ 中只有 $1$ 和 $-1$，那么相邻前缀和的差都恰好为 $1$，要想算出比 $s[i]-1$ 更小的数，必然会先算出 $s[i]-1$，那么这些更小数必然在 $s[i]-1$ 首次出现的位置的右边。
  

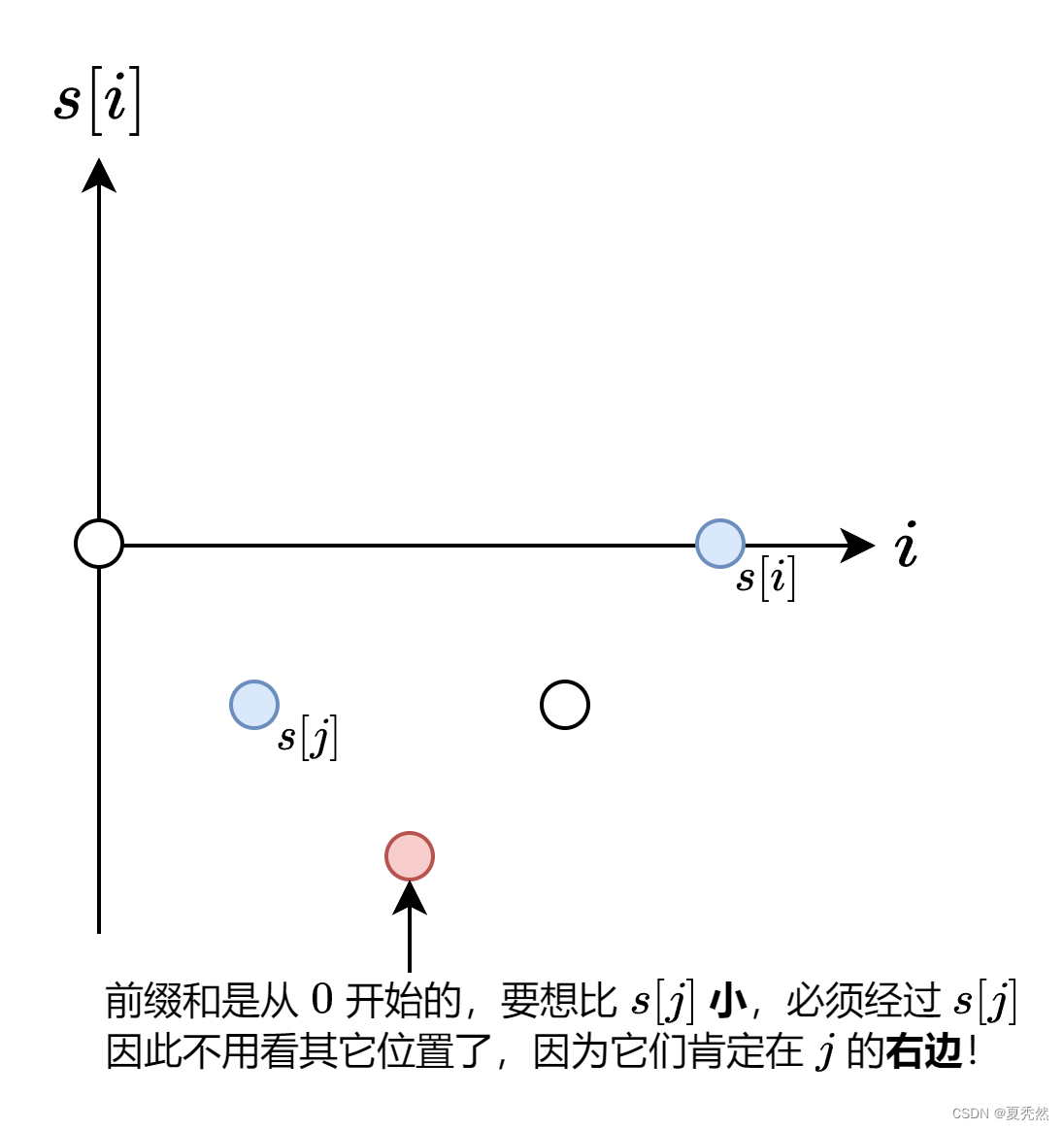
代码实现时，可以用哈希表记录每个 $s[i]$ 首次出现的下标。

不过，由于我们只需要考虑值在闭区间 $[-n,0]$ 内的前缀和，用数组记录是更加高效的。同时，为了避免用负数访问数组，可以在计算过程中把前缀和取反。

复杂度分析：

• 时间复杂度： $O(n)$，其中 $n$ 为 $\text{hours}$的长度。
• 空间复杂度： $O(n)$。

class Solution:
    def longestWPI(self, hours: List[int]) -> int:
        pos = [0] * (len(hours) + 2) # 记录前缀和首次出现的位置
        res = sums = 0
        for i, j in enumerate(hours, 1):
            sums += -1 if j > 8 else 1 # 取反，改为减法
            if sums < 0:
                res = i
            else:
                if pos[sums+1]: # 原本是 sums-1，取反改为 sums+1
                    res = max(res, i-pos[sums+1]) # 这里手写 if 会更快
                if pos[sums] == 0:
                    pos[sums] = i
        return res

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/longest-well-performing-interval/solutions/2110211/liang-chong-zuo-fa-liang-zhang-tu-miao-d-hysl/