👦个人主页：Weraphael
✍🏻作者简介：目前是C语言 + 算法学习者
✈️专栏：【C/C++】算法
🐋 希望大家多多支持，咱一起进步！😁
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 📂 加关注😍

---

前言

往期我们学习了高精度加法、高精度减法 和 高精度乘法，本站就是高精度算法最后一站了！闲言少叙，开快车🚝🚝

---

一、算法由来

前提：两个数都是正整数。当被除数的位数非常长时，再同时除以上位数较短的b。最后结果大到unsigned long long都存不了，这就要用到高精度除法。

二、算法基本思想

高精度算法同样也是计算机模拟人类竖式计算，并将其转化计算机语言的过程。

现在来回忆一下，小学除法我们是如何列竖式来解决的

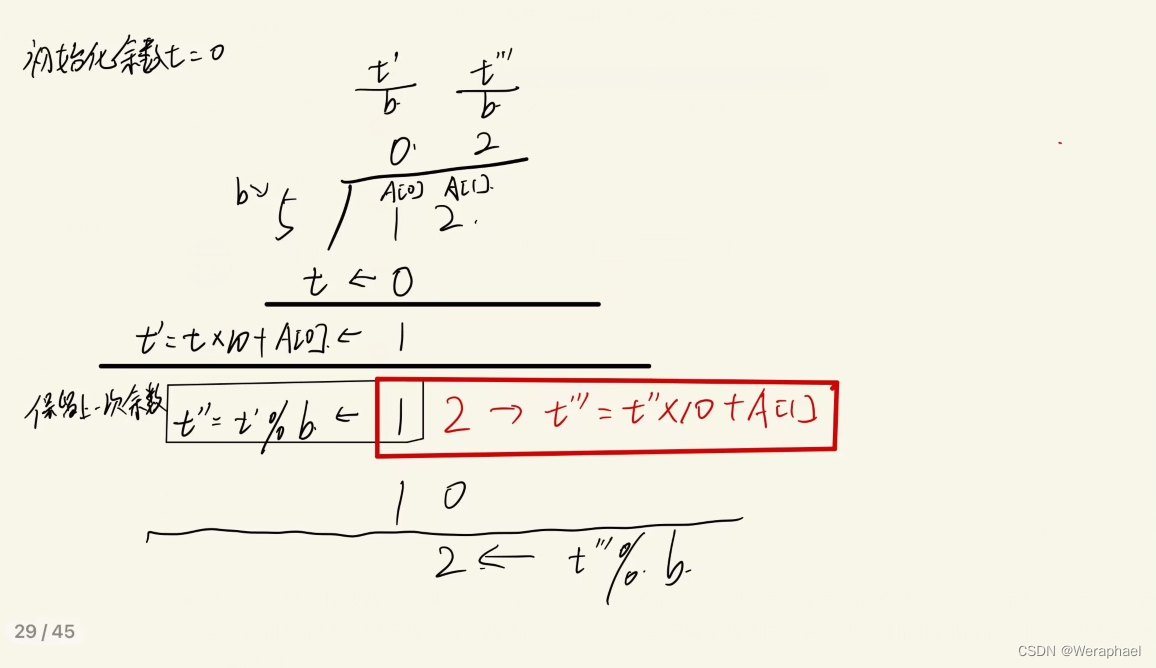
三、算法思路

• 首先，我们用数组存高精度数字（被除数）。为了方便读入，采用字符串读入。为什么要采用字符串读入呢？原因是数据位数过长。
• 其次，将其转化成数字存进vector<int>数组中。存进数组的时候一定要=倒着存入。
• 然后，就是两数相除的过程了，初始化余数t = 0，两数相除，t = t * 10 + A[i] ，t临时用来存储每一次余数的结果。
• 对于答案，只需要t / b即是商，为了保留上一步的余数t，只需要将t = t % b
• 再次重复以上操作，直到被除数全部都遍历完为止
• 在除法运算中，计算顺序是从高位向低位开始运算，因此A的前导0是在vector的前面而不是尾部（详情见算法基本思想），因此为了方便去除前导0，我们将A翻转，这样0就位于数组尾部，可以使用pop函数删除前导0
• 最后再逆序输出结果就是答案，输出t就是余数

四、代码模板

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

vector<int> div(vector<int> &A, int b, int &t)
{
    
    vector<int> C;//存储答案
    t = 0;//初始化余数为0
    
    //除法从高位开始算起
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        //上一次的余数乘10，再加上当前位上的数，就是被除数
        t = t * 10 + A[i];
        //商的计算
        C.push_back(t / b);
        //保留下一次的余数
        t %= b;
    }
    //翻转是为了方便取出前导0
    reverse(C.begin(), C.end());
    //去除前导0
    while (C.size() > 1 && C.back() == 0) 
    {
        C.pop_back();
    }
    //返回答案
    return C;
}

int main()
{
    string a;//字符串读入被除数
    int b; //除数
    int t; //余数
    vector<int> A; 

    //读入
    cin >> a >> b;
    
    //倒序存入A中
    for (int i = a.size() - 1; i >= 0; i -- ) 
    {
        A.push_back(a[i] - '0');
    }

    vector<int> C = div(A, b, t);

    //输出商
    for (int i = C.size() - 1; i >= 0; i -- ) 
    {
        printf("%d",C[i]);    
    }
    
    //输出余数
    printf("\n%d\n",t);

    return 0;
}