0 写在前面

机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖，由本人亲自从底层编写、测试与文章配套的各个经典算法，不依赖于现有库，可以大大加深对算法的理解。

🚀详情：机器学习强基计划(附几十种经典模型源码)

---

1 为什么要降维？

首先考虑单个特征的情形，假设在样本$x$任意小邻域$\delta$内都存在样本，则称对样本空间进行了密采样(dense sample)。例如取$\delta =0.01$，则在归一化样本平均分布的情况下需要采样100个样本。

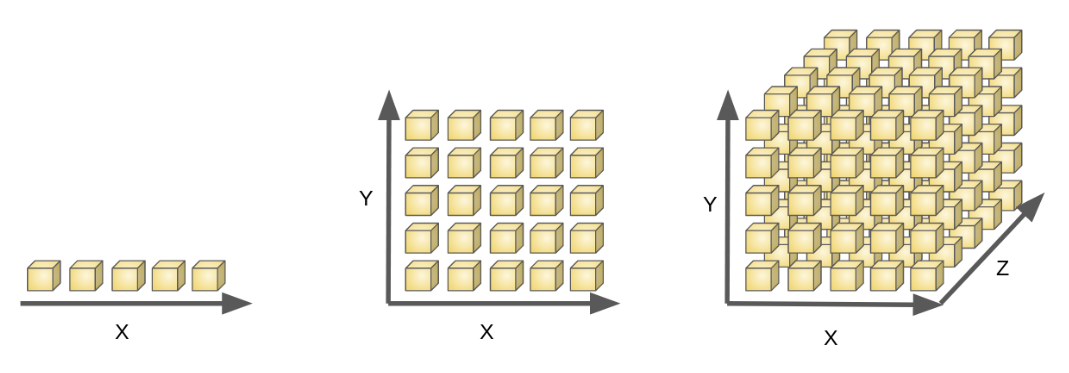
然而，机器学习任务中通常面临高维特征空间，若特征维数为40，则要实现密采样就需要$10^{80}$个样本——相当于宇宙中基本粒子的总数。所以密采样在高维特征空间中无法实现，换言之，高维特征样本分布非常稀疏，给机器学习训练、算法采样优化带来了困难。

这种高维情形下机器学习任务产生严重障碍现象称为维数灾难(curse of dimensionality)，维数灾难还会以指数级的规模造成计算复杂度上升、存储占用大等问题。缓解维数灾难的一个重要途径是降维(dimension reduction)，因为样本数据往往以某种与学习任务密切相关的低维分布的形式，嵌入在高维空间内，如图所示。

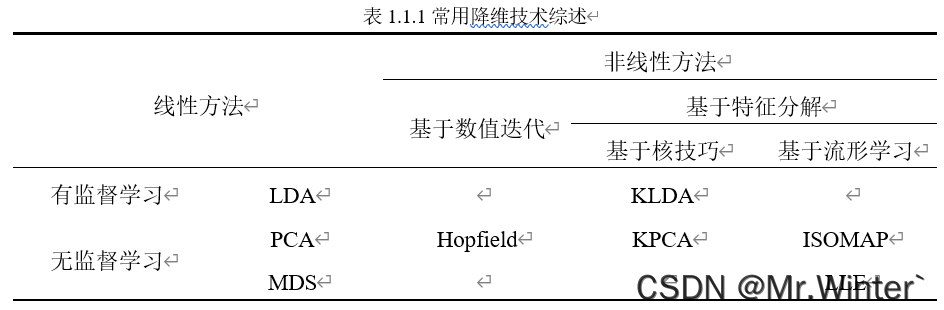
所以降维的核心原理是通过某种数学变换将原始高维特征空间转变为一个更能体现数据本质特征的低维子空间，在这个子空间中样本密度大幅提高，计算复杂度大幅降低，机器学习任务更容易进行。常见的降维技术如表所示

2 主成分分析原理

主成分分析(Principal Component Analysis, PCA)限制样本在经过降维映射$\mathbf{W}$得到的低维空间中具有最大可分性和特征最小相关性。

• 最大可分性：指高维样本在低维超平面上的投影应尽可能远离，因为越本质的特征越能将样本区分开
• 特征最小相关性：指量化样本属性的各个特征维度间应尽可能无关，因为特征间无关性越强构成的特征空间信息量越丰富。

满足这两个特性的特征在PCA算法中称为主成分。下面开始算法分析

假设样本$\mathbf{X}$经过中心化预处理，则其在低维超平面投影为${\mathbf{W}}^T\mathbf{X}$，投影协方差矩阵$\Sigma ={\mathbf{W}}^T{\mathbf{XX}}^T\mathbf{W}$，其中$\mathbf{W}=\left[\begin{array}{cccc}{\mathbf{w}}_1& {\mathbf{w}}_2& \cdots & {\mathbf{w}}_{d^{\prime }}\end{array}\right]$为低维空间的单位正交基。

• 考虑到最大可分性则应最大化$\Sigma$

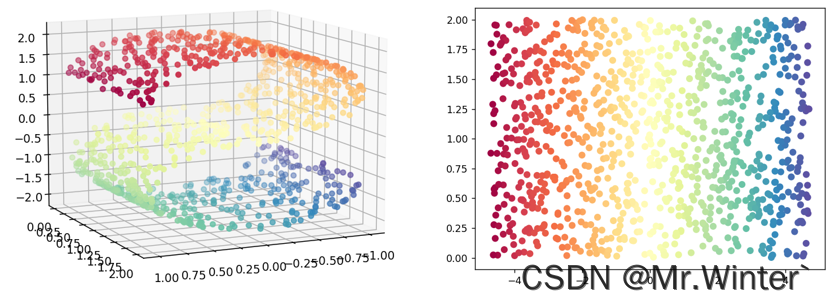
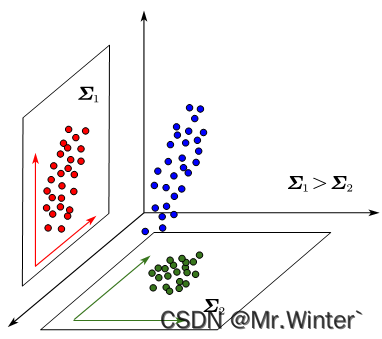
  我们从协方差的物理意义上思考一下为什么协方差小同类样本就接近。如图所示，是同一个三维样本在两个二维平面的投影，可以看出协方差大的样本越细长分散，协方差小则反之。所以协方差小可以使样本更聚合，也即样本投影点尽可能接近。更多协方差相关的内容请参考：机器学习强基计划1-4：从协方差的角度详解线性判别分析原理+Python实现

• 考虑到特征最小相关性则应最小化$\Sigma$的非对角线元素

综上所述，PCA的优化目标为

$$\underset{\mathbf{W}}{\max }\mathrm{tr}\left({\mathbf{W}}^T{\mathbf{XX}}^T\mathbf{W}\right)\mathrm{s}.\mathrm{t}.{\mathbf{W}}^T\mathbf{W}=\mathbf{I}$$

设拉格朗日函数为

$$\begin{array}{rl}L\left(\mathbf{W},\Theta \right)& =\mathrm{tr}\left({\mathbf{W}}^T{\mathbf{XX}}^T\mathbf{W}\right)+⟨\Theta ,{\mathbf{W}}^T\mathbf{W}-\mathbf{I}⟩\\ & =\mathrm{tr}\left({\mathbf{W}}^T{\mathbf{XX}}^T\mathbf{W}\right)+\mathrm{tr}\left({\Theta }^T\left({\mathbf{W}}^T\mathbf{W}-\mathbf{I}\right)\right)\end{array}$$

对降维映射$\mathbf{W}$的约束分为两个：${\mathbf{w}}_i^T{\mathbf{w}}_i=1,{\mathbf{w}}_i^T{\mathbf{w}}_j=0\left(i=1,2,\cdots ,d^{\prime },i\ne j\right)$

先考虑第一个单位化约束，则拉格朗日乘子矩阵退化为对角矩阵$\Lambda$。现令

$$\partial L\left(\mathbf{W},\Lambda \right)/\partial \mathbf{W}=2{\mathbf{XX}}^T\mathbf{W}+2\mathbf{W}\Lambda =0$$

即得${\mathbf{XX}}^T\mathbf{W}=-\mathbf{W}\Lambda$，考察每个${\mathbf{w}}_i$有

$${\mathbf{XX}}^T{\mathbf{w}}_i=-{\lambda }_i{\mathbf{w}}_i={\tilde{\lambda }}_i{\mathbf{w}}_i$$

所以$\mathbf{W}$是矩阵${\mathbf{XX}}^T\in {\mathbb{R}}^{d\times d}$进行特征值分解后对应的特征向量组成的矩阵，由于特征值分解可以通过施密特正交化等方式变换为正交矩阵，因此降维映射的${\mathbf{w}}_i^T{\mathbf{w}}_j=0$约束也成立。考虑到

$$\mathrm{tr}\left({\mathbf{W}}^T{\mathbf{XX}}^T\mathbf{W}\right)={\sum }_{i=1}^{d^{\prime }}{\mathbf{w}}_i^T{\mathbf{XX}}^T{\mathbf{w}}_i={\sum }_{i=1}^{d^{\prime }}{\tilde{\lambda }}_i{\mathbf{w}}_i^T{\mathbf{w}}_i={\sum }_{i=1}^{d^{\prime }}{\tilde{\lambda }}_i$$

因此取$d^{\prime }\ll d$个最大特征值对应的特征向量即可实现目标。

3 PCA与SVD的联系

PCA与SVD有一定联系：PCA降维需要求解协方差矩阵${\mathbf{XX}}^T$，而SVD分解的过程中需要求解${\mathbf{AA}}^T$与${\mathbf{A}}^T\mathbf{A}$，因此如果令$\mathbf{A}=\mathbf{X}$，那么SVD的过程中就能得到PCA所需的降维映射$\mathbf{W}$。

在大样本下${\mathbf{XX}}^T$或${\mathbf{AA}}^T$都将产生很高的复杂度，但SVD已有绕过计算${\mathbf{XX}}^T$或${\mathbf{AA}}^T$直接进行分解的高效算法，因此SVD通常作为求解PCA降维问题的工具，PCA体现了SVD分解中的一个方向(左奇异或右奇异)。

4 Python实现

PCA算法的复现非常简单，核心代码如下

'''
* @breif: 运行降维算法
* @param[in]: outDim -> 输出样本维数
* @retval: Z -> 低维样本集
'''          
def run(self, outDim):
    # 计算协方差矩阵
    cov = np.dot(self.X, self.X.T)
    # 特征值分解
    eigVal, eigVec = np.linalg.eig(cov)
    # 获取最大的d'个特征值对应的索引, np.argsort是按从小到大排序, 所以对特征值取负号
    index = np.argsort(-eigVal)[0:outDim]
    eigVec_ = eigVec[:, index]
    # 计算低维样本
    Z = np.dot(eigVec_.T, self.X)
    return Z

以鸢尾花数据集为例执行降维，效果如下

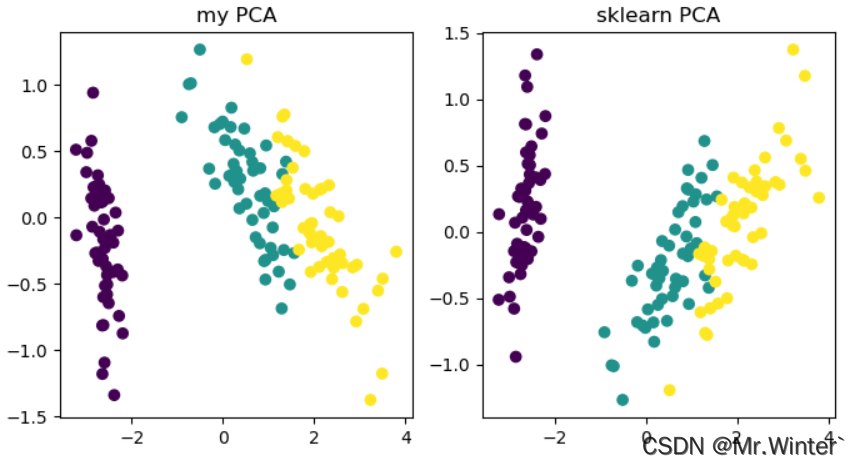
本文完整工程代码请通过下方名片联系博主获取

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇