欢迎关注「全栈工程师修炼指南」公众号

点击 👇 下方卡片 即可关注我哟!

设为「星标⭐」每天带你 基础入门 到 进阶实践 再到 放弃学习！

涉及 企业运维、网络安全、应用开发、物联网、人工智能、大数据 学习知识

“  花开堪折直须折，莫待无花空折枝。 ”

---

作者主页：[ https://www.weiyigeek.top ]

作者博客：[ https://blog.weiyigeek.top ]

作者答疑学习交流群：请关注公众号后回复【学习交流群】

---

文章目录:

计算机科学导论学习笔记

第 5 部分 数据安全与人工智能

17.计算理论

17.1 简单语言

• (1) 三条基本语句

• (2) 简单语言的威力

17.2 图灵机

• (1) 组成部分介绍

• (2) 简单语言的模拟

• (3) 邱奇-图灵论题

17.3 歌德尔数

• (1) 表示一个程序

• (2) 翻译一个数字

17.4 程序停止问题

17.5 问题复杂度

• (1) 不可解问题

• (2) 可解问题

温馨提示: 由于作者水平有限，本章错漏缺点在所难免，希望读者批评指正，若有问题或建议请在文章末尾留下您宝贵的经验知识，或联系邮箱地址

master@weiyigeek.top 或 关注公众号 [全栈工程师修炼指南] 留言。

---

计算机科学导论学习笔记

第 5 部分 数据安全与人工智能

此部分包含第15、16、17和18章，包含了计算机中传输的数据压缩(有损与无损)、网络数据在传输过程中如何保证其数据安全, 讨论计算理论，即哪些是可计算的，哪些是不可计算的，最后介绍当前热门的人工智能(AI)的观点，加深我们对计算机数据处理的的认识，为后续学习扩展基础认识。

17.计算理论

在前面几章中,我们把计算机看成是一台问题求解机器，在此章节我们冋答一些诸如此类的问题：

哪些问题可以通过计算机解决？语言之间是否存在优劣？运行一个程序前，是否可以确定该程序将要停止(终止)还是一直运行？用一种特定的语言解决一个问题需要多长时间？

为了回答这些问题，我们求助于一门学科：计算理论。

在学习计算理论前对其做一个简要的介绍。

• 首先，介绍一种语言，称为简单语言，通过它可以看到计算机解决任何问题所需要的最少语句是三条。

• 其次，介绍一种工具，一种称为图灵机的计算机模型，我们在第1章中提到过它。我们将看到，简单语言可以解决的问题也可以用图灵机解决。

• 第三，我们将证明没有任何程序可以知道另一个程序终止与否。证明本身表明有些问题计算机是无法解决的，最后简要地讨论算法的复杂性。本章中描绘的思想来自于计算机科学界的先驱们，如阿兰•图灵(Alan Turing),库尔特•哥德尔(Kurt Godel). 马文•明斯基(Marvin Minsky)、阿隆佐•邱奇(Alonzo Church)和斯蒂芬•科尔•克莱尼(Stephen Cole Kleene)。

17.1 简单语言

我们可以仅用三条语句来定义一种语言，它们是：递増语句、递减语句和循环语句, 在该语言中，只能使用非负整数数据类型。

这里不需要其他类型数据，因为本章的目标仅仅是说明计算理论中的一些思想。

(1) 三条基本语句

• 递增语句对变量加1: incr(x)

• 递减语句从变量中减1: decr(x)

• 循环语句是在变量的值不为0时，重复进行一个动作(或一系列动作)。

while(x){
  decr(x)
  Body of the loop
}

(2) 简单语言的威力

使用上述三种语句的简单程序设计语言和我们现在使用的任何一种复杂语言(比如C) 一样强大(虽然从效率来说不一定)，为了证明这一点，可以演示一下如 何模拟当今流行语言中的某些语句。

简单语言中的宏
此处，我们将每次模拟称为一个宏，并且在其他模拟中使用时不需要再重复其代码。

什么是宏?

宏(macro, macroinstruction 的简称)是高级语言中的一条指令，它等价于相同语言中的一条或多条指令的特定集合。

示例1.使用简单语言的语来给一变量X赋值为0(有时叫做清空变量), 第一个宏 X-0

while(x){
  decr(x)
}

示例2.使用简单语言的语句将一正整数赋值给变量X, 首先清空变量X，然后对X递增n次, 第二个宏: X-n。

X <- 0
incr(X)
incr(X)
...
incr(X)  // 重复n次

示例3.使用简单语言的语句将额外代码行来恢复X的值，第三个宏: Y <- X。

Y <- 0
while(X) {
  decr(X)
  incr(Y)
}

示例4.使用简单语言的语句将额外代码行来恢复X的值, 使其恢复原来的原始值，第四个宏: Y <- Y + X 。

while(X) {
  decr(X)
  incr(Y)
}

示例5.模拟简单语言中的宏,我们可使用加法宏因为整数的乘法可以用重复的加法来模拟，注意我们需要把X的值保存在一个临时变量中，因为在每次的加法中我们需要把的原始值加到Y上, 第五个宏: Y <- Y * X。

TEMP <- Y
Y <- 0
while(X) {
  decr(X)
  Y <- Y + TEMP
}

示例6.我使用宏来完成它因为整的指数可以用重复的乘法来模拟，第六个宏: Y <- Y^X

TEMP <- Y
Y <- 1
while(X) {
  decr(X)
  Y <- Y * TEMP
}

示例7.宏模了现代语言中的判断语 (if)在这个宏中，变量X的值只能是0或1这两个值之间的一个。如果的值不是0，在循环中A(一个动作或一系列动作)被执行。是该循只执行一次，因为第一轮行完后X的值变成0，从而跳出循环。如果的值是0循环被跳过，第七个宏: if X then A。

while(x) {
  decr(x)
  A
}

当然除此之外，还有需要其他宏，但是很显然，我们需要更多的宏来使简单语言与现代语言相匹配，建立其他宏是可能的，但却并不简单（较复杂）。

输入和输出
描述: 在简单语言中 Read X 语句 可以使用（X←n）来模拟，我们也可模拟输出，即假定程序中使用的最后一个变量保存着将要打印的数据, 记住这不是实际的语言，而是仅仅用来证明计算机科学中的一些定理。

17.2 图灵机

图灵机是在1936年由Alan M.Turning提出用来解决可计算问题的, 它是现代计算机的基础。

(1) 组成部分介绍

图灵机由三部分组成：磁带、控制器和读/写头（如下图所示）。

磁带
尽管现代计算机中使用的随机存储设备容量是有限的，但我们假定图灵机中的内存是无限的，磁带任何时候只能保存一系列顺序字符，该字符来自计算机所能接收的字符集中。

为了我们的目的，假设图灵机只能接收两个符号：空白（b）和数字1，下述给出了这种机器磁带记录数据的一个例子。

磁带左手的空白定义了存储在磁带上的非负整数的开始，一个整数用1构成的串表示。磁带右手的空白定义了整数的结束。磁带的其他部分包含了空白字符。如磁带上存有多个整数，它们用至少一个空白字符隔开。

此外，还假设磁带处理一元算术中的正整数, 在一元算术中，正整数仅由1组成，例如整数4表示为1111 （4个1）, 7表示为1111111 （7个1）,没有1的地方表示0。

读/写头
描述: 在任何时刻总是指向磁带上的一个符号，我们称这个符号为当前符号，读/写头每次在磁带上读写一个符号。每读写完一次后，它向左移、向右移, 读、写和移动都是在控制器指令下进行的。

控制器

控制器是理论上功能作用类似于现代计算机中央处理单元（CPU）的一个部件，它是一个有限状态自动机，即该机器有预定的有限个状态并能根据输入从一个状态转移到另一个状态，但任何时候它只能处于这些状态中的一种。

下图给出了简单控制器作为有限状态自动机控制器的状态转移图。

在此图中, 自动机有三个状态（A、B和C）,虽然控制器通常有很多状态。图中给出了读入字符后所引起状态的改变, 每一行上的表达式（x/y/L, x/y/R 和 x/y/N ）显示了：控制器读入x后，它写符号y（改写x）,并将读/写头移到左边（L）、右边（R）或不动（N）。注意既然磁带上的符号只有空白或数字1,那么从每个状态出去的路径只有两条：要么读到的是空白符号，要么读到的是数字1。线（称为转移线）的起点显示的是当前状态，线的末端（箭头）显示的是一下状态。

我们可以建立一个每一行代表一个状态的状态转移表（表17-1）。

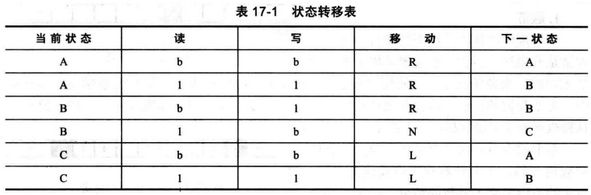
表有5栏表示当前状态、读入符号、所写符号、读/写头的移动方向和下一个符号，既然机器只能经历有限个状态, 那么我们能创建一个像我们在第5章中为简单计算机建立的指令集。

指令是把一行中的5列值放在一起，对于这台初级的机器，我们只有6条指令:

1.（A, b, b, R, A）3.（B, b, 1, R, B） 5.（C, b, b, L, A）
2.（A, 1, 1, R, B）4.（B, 1, b, N, C） 6.（C, 1, 1, L, B）

例如，第一条指令是说：如果机器处于状态A, 读到了符号b, 它就用一个新的b改写符号，读/写头向右移到下一个符号上，机器的状态转移到状态A也就是保留在相同的状态中。

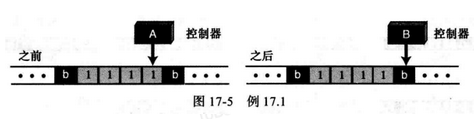
例如，一个图灵机只有两个状态和如下的4条指令：1.(A, b, b, L, A) 2.(A, 1, 1, R, B) 3.(B, b, b, L, A) 4.(B, 1, b, R, A).

• 开始时, 机器是处于状态A,当前符号是1,这就意味着只有第二条指令(A, 1, 1, R, B) 能被执行。

• 最后时, 注意控制器的状态已经变成了B,读/写头已经向右移动了一个符号。

---

偷偷的告诉你哟？【极客全栈修炼】微信小程序已经上线了，

可直接在微信里面直接浏览博主博客了哟，后续将上线更多有趣的小工具。

---

(2) 简单语言的模拟

在图灵机中，我们能编写程序来实现简单的语句了，值得注意的是这些语句可以用多种方法来写，为了学习的目的，我们选择了最简单或最方便的，但它们不一定是最好的。

1.incr(X)语句的图灵机
控制器有4个状态，从S1到状态S4,状态S1是开始状态，状态S2是右移的状态，状态S3是左移的状态，状态S4是停机状态。如果到达停止状态，机器就停止：没有指令从这个状态开始。

2.decr(X)语句的图灵机
此处，我们使用最小的指令数目来实现decr(X)语句, 其原因是我们在下一条语句(while循环)中要用到这个语句，它也被用来实现所有的宏。

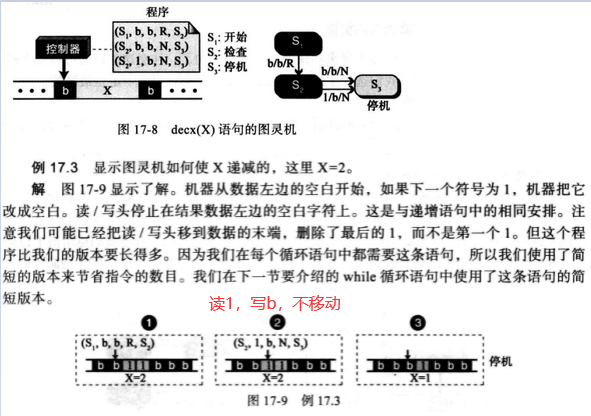
3.while语句的图灵机
为了模拟循环，我们假定X和循环体处理的数据存储在磁带上，中间以单个空白字符相隔，三个状态 Si、S和 S;控制了循环，它通过判断的值，如果X=0，就退出循环。把这三个状态与图 17-8 中减语句中使用的三个状态进行比较。状态 M把读/写头移过在每次重复中在处理数据开始时定义了数据开始位置的空白符号:状态M把读/写头移过在每次重复中在处理数据结束时定义了X的开始位置的空白符号;状态Bs定义了循环体的开始状态，而状态 B定义了循环体的停机状态。循环体在这两个状态间可能有几个状态。

下图中，还显示了语句的重复性质，状态图本身是一个只要X的值不为0就重复的循环，当X的值变成0,循环停止，状态S3 (停机状态)到达了。

(3) 邱奇-图灵论题

上面我们演示了图灵机能模拟简单语言中的三个基本语句，也就意味着图灵机能模拟我们为简单语言定义的所有的宏。

那么图灵机是否能解决一台计算机能解决的任何问题？

这个问题的答案可以在邱奇-图灵论题(Church-Turing thesis)中找到。

基于这样的观点，能用写一个算法来完成的任何符号操纵任务也可以用图灵机完成。注意这只是论题，不是定理, 定理可以在数学上得到证明，但论题却不能, 虽然这个论题可能永远得不到证明，但有些强有力的论断在支持它。

• 首先，尚未发现有图灵机不能模拟的算法；

• 其次，所有在数学上已经得到证明的计算机模型都与图灵机模型等价，这个论断是得到证明的。

17.3 歌德尔数

在计算机科学理论中，一个无符号数能被分配给任何用特定语言编写的程序，通常称为歌德尔数（用澳大利亚数学家Kurt G6del命名）, 这种分配有很多优点。

首先，程序可以作为单一数据项输入给其他程序。第二，程序可以通过它的整数表示来引用。第三，该编号方式可以用来证明有一些问题计算机并不能解决，从而说明世界上问题的数量远远比曾经编写的程序数量要多得多。

各种各样的方法被设计用来给程序编号, 我们用一个简单的变换给用简单语言编写的程序编号。假定简单语言仅使用15个标志符（表17-2 ）

注意，在这种语言当中仅使用X, X1. X2,…，X9。作为变量。为了将变量编码，将Xn看成是由X和n两个符号组成来处理（X3是由X和3组成）。如果在宏中有其他类型变量，应将它们转换为Xn的形式。

(1) 表示一个程序

运用这个表，我们可以通过唯一的正整数表示用简单语言编写的任何程序, 按照以下步骤进行：
1）将每一个符号用表中所给的对应十六进制代码替代。
2）将最后的结果（十六进制）转化为无符号整数。

例如，对于incr(X)来说，用对应的十六进制代码替代每个符号, 此程序可以用数字175表述。

incr X -> (AF)16 -> 175

(2) 翻译一个数字

为了证明编号方式是唯一的，用以下步骤来解释歌德尔数：
1）将数字转换成十六进制数。
2）用表17-2将每个十六进制数翻译成对应的符号(忽略0 )。

注意，虽然用简单语言编写的一切程序都能用数字表述，但是，并不是所有的数字都能解释为合法程序。转换之后，如果符号不符合语法规则，这个数字就不是有效的程序。

例如，将 3058 翻译成程序，即将数字变成十六进制数并使用相应的符号代替。

3058 -> (BF2)16 -> decr X 2 -> decr (X2)

17.4 程序停止问题

几乎所有的简单语言编写的程序都包含某种形式的重复(循环或递归函数)。

一个重复结构可能永远都不会结束(停机)，这就是说一个含有无限循环的程序可以永远运行，但是程序开发者通常需按照需求进行设置跳出循环条件，否则可能导致死循环(严重时会导致系统崩溃😫)。

例如，下面的用简单语言编写的程序可以永不结束。

x = 1
while (x) {}

我们能编写一个程序来测试任何可以用哥德尔数表示的程序是否会终止吗?

答: 经过计算机科学家证实，停机问题是不可能解决的。

17.5 问题复杂度

既然我们已经证明, 至少有一个问题计算机无法解决，那么让我们在这个问题上再进一步深入。

在计算机科学领域，我们可以这么说，一般来说问题可以分为两类：可解问题和不可解问题,而可解问题又可以分为两种：多项式问题和非多项式问题。

(1) 不可解问题

描述: 无法用计算机解决的问题有无穷无尽，停机问题是其中一个。

要证明一个问题是无法解决的，方法是证明如果它可以解决，那么停机问题也同样可以解决，换句话说，证明一个问题能否解决等同于证明停机问题能否解决。

亲，文章就要看完了，不关注一下作者吗？

(2) 可解问题

描述: 能够被计算机解决的问题也是无穷无尽，平常我们关心的是：计算机需要花多长时间去解决一个问题。换言之，这个问题有多复杂？

问题的复杂度可以用不同的方法衡量，例如，运行时间、需要的内存等，其中一种衡量方法是运行时间，即运行一个程序需要花多长时间？

衡量可解问题复杂度的一个方法是找出计算机运行该程序时要执行的运算数量。

这样，复杂度问题不是依赖于运行程序的计算机速度，而是依赖于输入的数目。

例如，如果程序在处理一个列表(例如对列表中元素进行排序)，则复杂度依赖于该列表中元素的数目，通是使用大 O 表示法。

大 O 表示法
通常我们会使用大O表示法来表示，算法代码片段的执行效率，在该表示法中，运行数量(或者一系列相关运算)，表示为输入量的函数。

例如, 符号 O(n) 表示有n个输入, 执行 n 次运算，符号 O(n^2) 表示有n个输入，执行n^2次运算。

多项式问题
如果程序的复杂度为 0(logn)、O(n)、O(n^2) 或 O(n^k)(k为常数)，则被称为多项式问题。

以当今计算机的处理速度，对于一个有合理输入数量 的(如从1000到1000 000) 的多项式问题我们都能解决。

非多项式问题
如果一个程序的复杂度远比多项式问题复杂, 例如 0(10^n) 或 O(n!)，当输入数很小(小于 100)时，这种问题可以解决。

如果输入数很大，则需要坐在计算机面前等上几个月的时间才能看到非多项式问题的解决结果。

但是，随着计算机处理速度的不断提高，我们也许能在更短的时间内解决非多项式问题。

原文地址: https://blog.weiyigeek.top/2023/1-18-708.html

本文至此完毕，更多技术文章，尽情等待下篇好文！

 学习书籍推荐 往期发布文章 

持续集成案例之使用Docker运行自构建Jenkins的Agent镜像固定工作节点实践（分享企业项目流水线代码）

记一次由于外部K8S集群证书到期导致Jenkins无法生成动态agent节点错误解决（入坑出坑）

运维案例之记一次Kubernetes集群证书过期或延期操作处理实践指南（干货分享）

长按（扫描）二维码  获取更多渠道哟!

如果此篇文章对你有帮助，请你将它分享给更多的人！

 点击【"阅读原文"】获取更多有趣的知识!