【数据结构】基础：图的基本概念与实现（附C++源代码）

摘要：将会在数据结构专题中开展关于图论的内容介绍，其中包括四部分，分别为图的概念与实现、图的遍历、图的最小生成树以及图的最短路径问题。本文将介绍图的基本概念以及相关内容，再对图的常见实现方式进行介绍。实现方法为邻接矩阵法与邻接表法，从其成员实现、构造、边的添加出发，最后对二者进行比较。

文章目录

【数据结构】基础：图的基本概念与实现（附C++源代码）
- 一、图的基本概念
- - 1.1 图的定义
  - 1.2 图的相关概念
- 二、图的实现
- - 2.1 邻接矩阵
  - - 2.1.1 成员实现
    - 2.1.2 构造函数
    - 2.1.3 边的添加
    - 2.1.4 打印函数
    - 2.1.5 测试用例
  - 2.2 邻接表
  - - 2.2.1 成员实现
    - 2.2.2 构造函数
    - 2.2.3 边的添加
    - 2.2.4 打印函数
    - 2.2.5 测试用例
  - 2.3 对比

一、图的基本概念

1.1 图的定义

图是由顶点集合及顶点间的关系组成的一种数据结构：G = (V， E)，其中：

顶点集合V = {x|x∈G中顶点}，V(G)表示图G中顶点的有限非空集；
边集合E = {(x,y)|x,y∈V}或者E = {<x, y>|x,y∈V && Path(x, y)}，E(G)是顶点间关系的有穷集合，也叫做边的集合。(x, y)表示x到y的一条双向通路，即(x, y)是无方向的；Path(x, y)表示从x到y的一条单向通路，即Path(x, y)是有方向的。

1.2 图的相关概念

顶点和边：图中结点称为顶点，第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边，图中的第k条边记作ek，ek = (vi，vj)或<vi，vj>。

有向图和无向图：

在有向图中，顶点对<x, y>是有序的，顶点对<x，y>称为顶点x到顶点y的一条边(弧)，<x, y>和<y, x>是两条不同的边。

在无向图中，顶点对(x, y)是无序的，顶点对(x,y)称为顶点x和顶点y相关联的一条边，这条边没有特定方向，(x, y)和(y，x)是同一条边。注意：无向边(x, y)等于有向边<x, y>和<y, x>。

完全图：

无向完全图：在有n个顶点的无向图中，若有n * (n-1)/2条边，即任意两个顶点之间有且仅有一条边

有向完全图：在n个顶点的有向图中，若有n * (n-1)条边，即任意两个顶点之间有且仅有方向相反的边

邻接顶点：在无向图中G中，若(u, v)是E(G)中的一条边，则称u和v互为邻接顶点，并称边(u,v)依附于顶点u和v；在有向图G中，若<u, v>是E(G)中的一条边，则称顶点u邻接到v，顶点v邻接自顶点u，并称边<u, v>与顶点u和顶点v相关联。

顶点的度：顶点v的度是指与它相关联的边的条数，记作deg(v)。

对于有向图，顶点的度等于该顶点的入度与出度之和，其中顶点v的入度是以v为终点的有向边的条数，记作indev(v);顶点v的出度是以v为起始点的有向边的条数，记作outdev(v)。因此：dev(v) = indev(v) + outdev(v)。

对于无向图，顶点的度等于该顶点的入度和出度，即dev(v) = indev(v) = outdev(v)。

路径：在图G = (V， E)中，若从顶点vi出发有一组边使其可到达顶点vj，则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径。

路径长度：对于不带权的图，一条路径的路径长度是指该路径上的边的条数；对于带权的图，一条路径的路径长度是指该路径上各个边权值的总和。

子图：设图G = {V, E}和图G1 = {V1，E1}，若V1属于V且E1属于E，则称G1是G的子图。

连通图：在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图。

强连通图：在有向图中，若在每一对顶点vi和vj之间都存在一条从vi到vj的路径，也存在一条从vj到vi的路径，则称此图是强连通图。

生成树：一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。

二、图的实现

对于图的实现，需要反映顶点集和边集的信息，可以采取不同的图结构和算法，主流方法有两种，分别为邻接矩阵和邻接表。以下将对该方式进行说明，并对其进行比较。

2.1 邻接矩阵

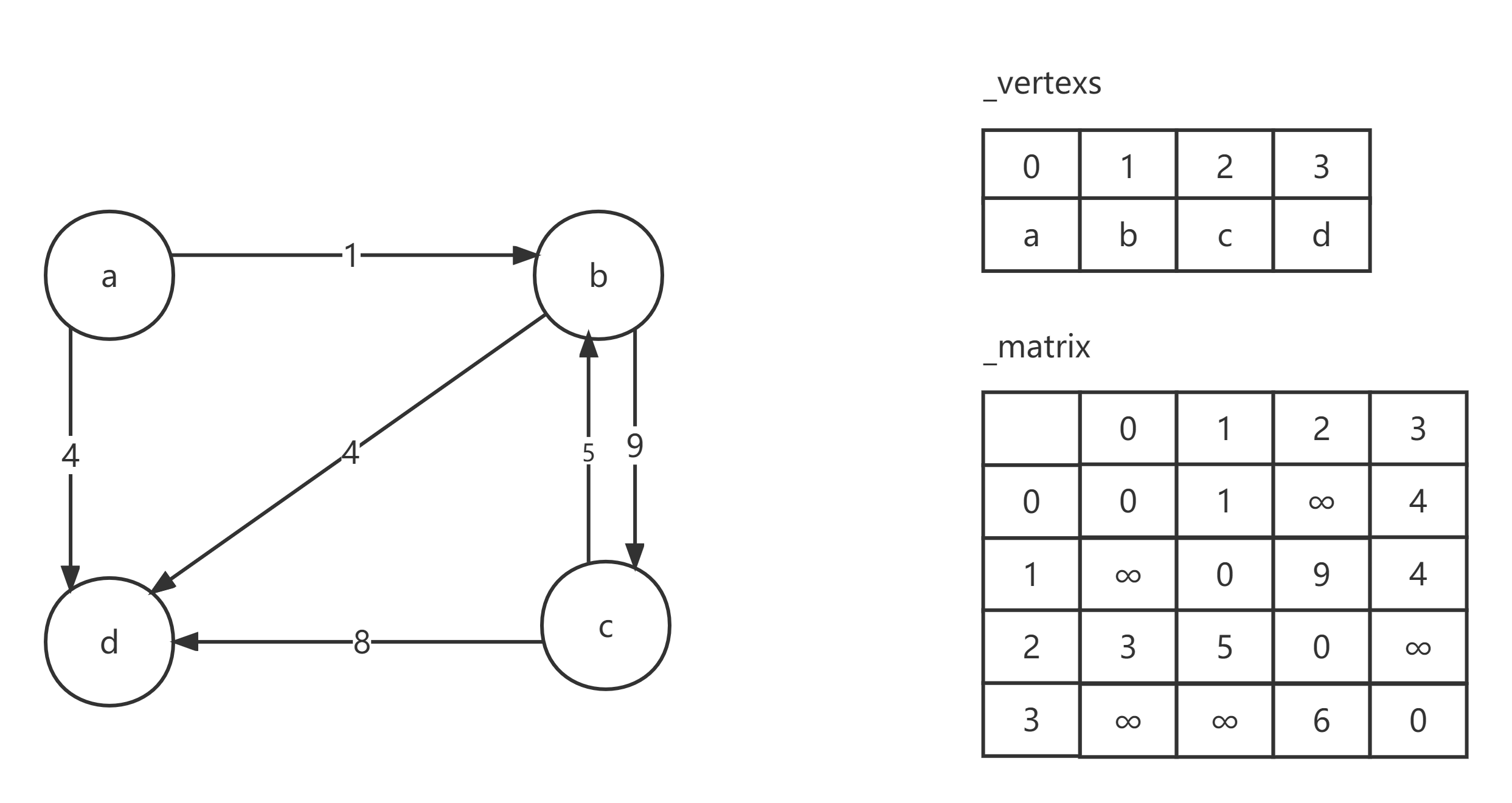
邻接矩阵法是通过一个二维数组及其他附属数据结构完成对于图的存储，具体内容如下：

一维数组：记录顶点及其元素，每个顶点都对应着一个检索，该检索通过一棵树进行储存在这里采用了map
索引树：记录了数组索引和顶点元素之间的关系
二维矩阵：表示顶点之间边的关系，可以记录为是否连通或记录两点之间的权重

2.1.1 成员实现

在此使用C++实现，其中添加了Direction 表示是否为有向图，MAX_WEIGHT表示最大权值

template<class V, class W, bool Direction = false, W MAX_WEIGHT = INT_MAX>
    class Graph {
        private:
        vector<V> _vertexs; // 顶点集合
        map<V, int> _vIndexMap; // 顶点检索
        vector<vector<W>> _matrix; // 邻接矩阵
    };

2.1.2 构造函数

对于图的初始化构建，将容量进行对于n个结点的扩容，将节点元素写入，并将结点元素与对应的索引记录再map中。对于矩阵而言，形成n × n的扩容，赋初值为最大权值，在有些实现方法中，会对图的对角线进行取零也是可以的，在此不进行该操作。

Graph() = default;
/// <summary>
/// _vertexs扩容即可
/// _matrix赋初值Max_Weight 对角线为0
/// </summary>
Graph(const V* vertexs,size_t vertexSize) {
    _vertexs.reserve(vertexSize);
    for (size_t i = 0; i < vertexSize; i++) {
        _vertexs.push_back(vertexs[i]);
        _vIndexMap[vertexs[i]] = i;
    }
    // 格式化
    _matrix.resize(vertexSize);
    for (auto& e : _matrix) {
        e.resize(vertexSize, MAX_WEIGHT);
    }
    // 对角线写0
    //for (size_t i = 0; i < _matrix.size(); i++) {
    //	_matrix[i][i] = 0;
    //}
}

2.1.3 边的添加

实现图边添加的方式主要有三种，分别为基础IO、文件添加以及函数调用。在此使用函数调用的方式，而具体实现方式是在邻接矩阵写入对应权值即可。对于有向与无向而言，无向图需要在对称位置写入对称的权值，具体代码如下：

/// <summary>
/// 在map中检索对应的索引
/// </summary>
/// <param name="v">顶点中的元素</param>
/// <returns>检索值</returns>
size_t GetVertexIndex(const V& v) {
    auto ret = _vIndexMap.find(v);
    if (ret != _vIndexMap.end()) {
        return ret->second;
    }
    else {
        throw invalid_argument("不存在的顶点");
        return -1;
    }
}
/// <summary>
/// 添加边 找出索引调用函数AddEdgeByIndex
/// </summary>
/// <param name="src">起点元素</param>
/// <param name="dest">终点元素</param>
/// <param name="weight">权重</param>
void AddEdge(const V& src, const V& dest, const W& weight) {
    size_t srcIndex = GetVertexIndex(src);
    size_t destIndex = GetVertexIndex(dest);
    AddEdgeByIndex(srcIndex, destIndex, weight);
}
/// <summary>
/// 在矩阵中写入对应权值
/// 无向图需要再写入对称位置
/// </summary>
/// <param name="srcIndex">起点检索</param>
/// <param name="destIndex">终点检索</param>
/// <param name="weight">权重</param>
void AddEdgeByIndex(size_t srcIndex, size_t destIndex, const W& weight){
    _matrix[srcIndex][destIndex] = weight;
    if (Direction == false) {
        _matrix[destIndex][srcIndex] = weight;
    }
}

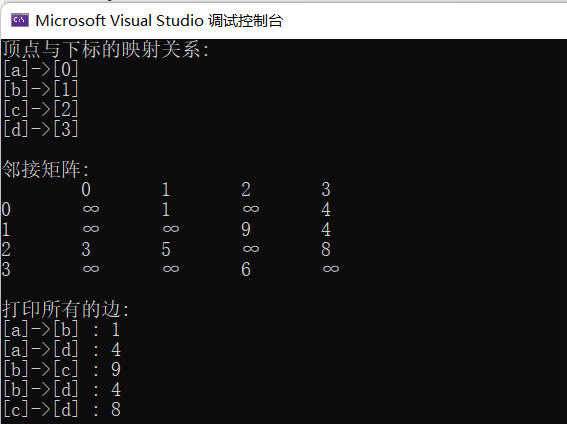
2.1.4 打印函数

打印顶点和下标映射关系
打印矩阵
打印所有的边

void Print() {
    // 打印顶点和下标映射关系
    cout << "顶点与下标的映射关系:" << endl;
    for (size_t i = 0; i < _vertexs.size(); ++i) {
        cout << "[" << _vertexs[i] << "]" << "->" << "[" << i << "]" << endl;
    }
    cout << endl;

    cout << "邻接矩阵:" << endl;
    cout << " \t";
    for (size_t i = 0; i < _vertexs.size(); ++i) {
        cout << i << "\t";
    }
    cout << endl;
    // 打印矩阵
    for (size_t i = 0; i < _matrix.size(); ++i) {
        cout << i << "\t";
        for (size_t j = 0; j < _matrix[i].size(); ++j) {
            if (_matrix[i][j] == MAX_WEIGHT)
                cout << "∞" << "\t";
            else
                cout << _matrix[i][j] << "\t";
        }
        cout << endl;
    }
    cout << endl;

    // 打印所有的边
    cout << "打印所有的边:" << endl;
    for (size_t i = 0; i < _matrix.size(); ++i) {
        for (size_t j = 0; j < _matrix[i].size(); ++j) {
            if (i < j && _matrix[i][j] != 0 && _matrix[i][j] != MAX_WEIGHT) {
                cout << "[" << _vertexs[i] << "]" << "->" << "[" << _vertexs[j] << "] : " << _matrix[i][j] << endl;
            }
        }
    }
}

2.1.5 测试用例

void TestGraph(){
	Graph<char, int, true> g("abcd", 4);
	g.AddEdge('a', 'b', 1);
	g.AddEdge('a', 'd', 4);
	g.AddEdge('b', 'd', 4);
	g.AddEdge('b', 'c', 9);
	g.AddEdge('c', 'd', 8);
	g.AddEdge('c', 'b', 5);
	g.AddEdge('c', 'a', 3);
	g.AddEdge('d', 'c', 6);

	g.Print();
}

2.2 邻接表

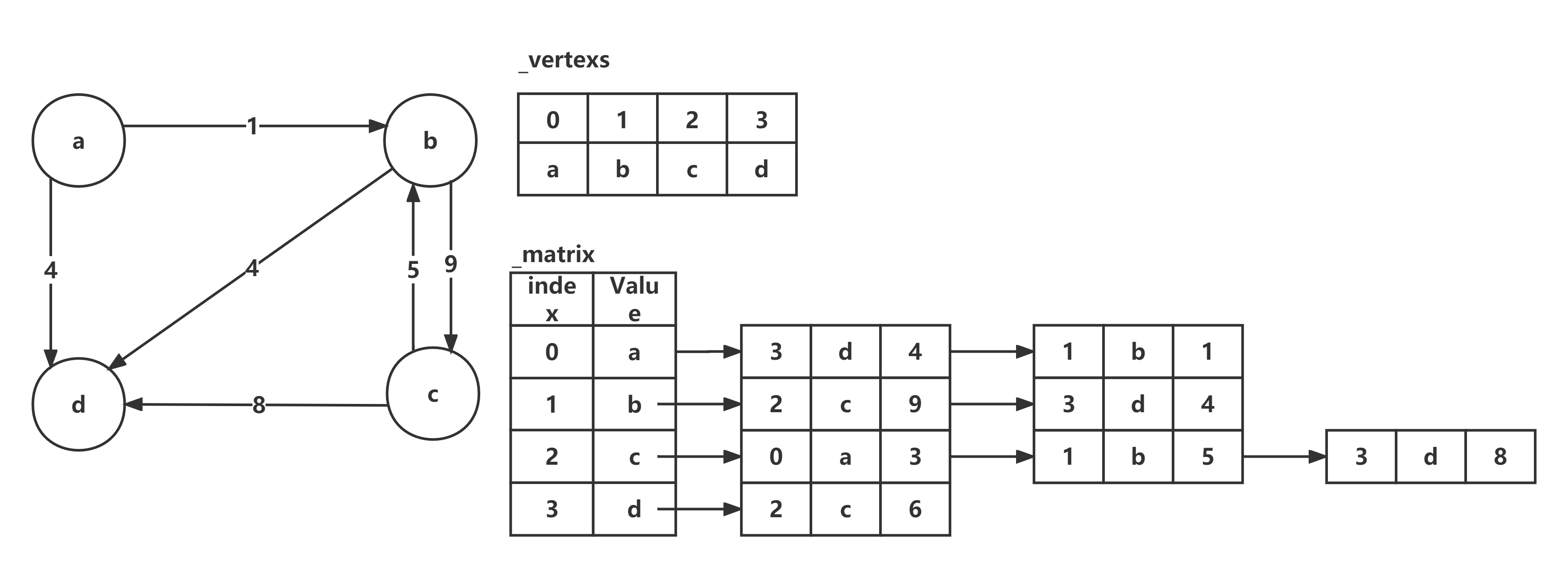
邻接矩阵法是通过一个二维数组及其他附属数据结构完成对于图的存储，具体内容如下：

一维数组：记录顶点及其元素，每个顶点都对应着一个检索，该检索通过一棵树进行储存在这里采用了map
索引树：记录了数组索引和顶点元素之间的关系
邻接表：通过数组进行储存，索引下标对应顶点，每个数组元素为一个链表，记录与该点连接的边

2.2.1 成员实现

在此使用C++实现，其中添加了Direction 表示是否为有向图，由于后续需要对边进行插入，因此需要进行封装。

template<class V,class W,bool Direction = false>
    class Graph {
        typedef Edge<W> Edge;
        private:
        vector<V> _vertexs;
        map<V, int> _indexMap;
        vector<Edge*> _linkTables;
    };
template<class W>
    class Edge {
        public:
        int _destIndex;
        W _weight;
        Edge<W>* _next;

        Edge(int destIndex,const W& weight) 
            :_destIndex(destIndex)
                ,_weight(weight)
                ,_next(nullptr)
            {}
    };

2.2.2 构造函数

对于图的初始化构建，将容量进行对于n个结点的扩容，将节点元素写入，并将结点元素与对应的索引记录再map中。对于邻接表而言，进行扩容并存储空指针，在后续过程中会进行插入。

Graph(const V* arrV, size_t vSize){
    _vertexs.reserve(vSize);
    for (size_t i = 0; i < vSize; i++) {
        _vertexs.push_back(arrV[i]);
        _indexMap[arrV[i]] = i;
    }
    _linkTables.resize(vSize, nullptr);
}

2.2.3 边的添加

获取边的插入，进行检索顶点，在邻接表中找出对应的位置，对应链表来说，为了提高效率进行头插操作。而对于无向图还需要在目标节点的链表上也添加边，具体代码如下：

size_t GetVertexIndex(const V& value){
    auto it = _indexMap.find(value);
    if (it != _indexMap.end()){
        return it->second;
    }
    else{
        throw invalid_argument("顶点不存在");
        return -1;
    }
}
void AddEdge(const V& src, const V& dest, const W& weight) {
    size_t srcIndex = GetVertexIndex(src);
    size_t destIndex = GetVertexIndex(dest);
    // 链表头插
    Edge* edge = new Edge(destIndex, weight);
    edge->_next = _linkTables[srcIndex];
    _linkTables[srcIndex] = edge;
    // 对称插入
    if (Direction == false) {
        Edge* edge = new Edge(srcIndex, weight);
        edge->_next = _linkTables[destIndex];
        _linkTables[destIndex] = edge;
    }
}

2.2.4 打印函数

打印对应的顶点与检索信息，再打印邻接表的内容，代码如下：

void Print(){
    // 顶点
    for (size_t i = 0; i < _vertexs.size(); ++i){
        cout << "[" << i << "]" << "->" << _vertexs[i] << endl;
    }
    cout << endl;

    for (size_t i = 0; i < _linkTables.size(); ++i){
        cout << _vertexs[i] << "[" << i << "]-> ";
        Edge* cur = _linkTables[i];
        while (cur){
            cout << "[" << _vertexs[cur->_destIndex] << "|" << cur->_destIndex << "|" << cur->_weight << "]->";
            cur = cur->_next;
        }
        cout << "nullptr" << endl;
    }
}

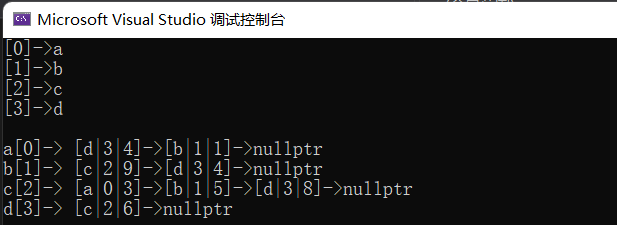
2.2.5 测试用例

void TestGraph(){
	linkTable::Graph<char, int, true> g("abcd", 4);
	g.AddEdge('a', 'b', 1);
	g.AddEdge('a', 'd', 4);
	g.AddEdge('b', 'd', 4);
	g.AddEdge('b', 'c', 9);
	g.AddEdge('c', 'd', 8);
	g.AddEdge('c', 'b', 5);
	g.AddEdge('c', 'a', 3);
	g.AddEdge('d', 'c', 6);
	g.Print();
}

2.3 对比

内容比较	邻接矩阵	邻接表
适用场景	稠密图	稀疏图
优点	通过下标判断两点间的邻接关系并获得权值	适用于查找一个顶点连接出去的边
缺点	相对而言不适用于查找一个顶点连接所有边	不适用于确定两个点是否连接及权值
空间复杂度	O(\|V\|^2)	O(\|V\|+\|E\|)