---

力扣435. 无重叠区间

题目链接：435. 无重叠区间

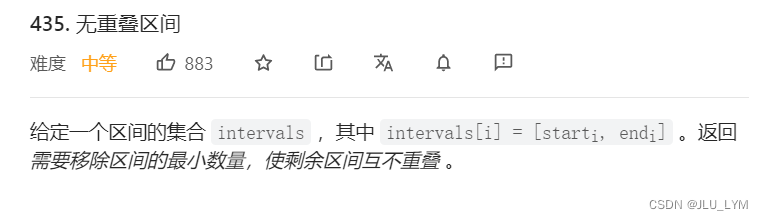
思路

1、贪心策略：

1、题目中，给了若干个区间，现在，我想留下尽可能多的，不重叠的区间
2、考虑，一个区间，无非就是，起点终点，一定要避免一个误区，就是二者一起考虑，这样不利于制定贪心策略，尤其是遇到这种，多条件的，最开始想的时候，一定要分开考虑，再进行适当的合并
3、所以，按照上面的思路，要么考虑起点，要么考虑终点
4、比如说所有区间都在[1,10]，[1,9],[1,2]明显的，选后者能剩余出更多的地方容纳别的区间，是满足题意得
5、综上，起点并不能决定是否能帮助容纳更多区间，只有终点可以，越早结束，那么就会留下更多的地方容纳更多的区间
6、所以，我们按照终点进行排序，我们从小到大选择出不重叠的所有区间即可

2、因为是vector<vector> ,sort函数不能直接用，需要自定义比较方法，有如下几种方式

<1>单独写出来

// 比较器函数
bool compare(参与比较的第一个元素, 参与比较的第二个元素)
{
    return 参与比较的第一个元素 > 参与比较的第二个元素; // 降序
    // return 参与比较的第一个元素 < 参与比较的第二个元素; 升序
}
 
// sort函数
void sort(排序的首地址, 排序的末地址 + 1, 比较器函数名称);

<2>写在sort函数内部

		sort(intervals.begin(), intervals.end(), [](const auto& a, const auto& b) {
			return a[1] < b[1];
		});

代码

class Solution {
public:
	int eraseOverlapIntervals(vector<vector<int>>& intervals) {
		int n = intervals.size();
		sort(intervals.begin(), intervals.end(), [](const auto& a, const auto& b) {
			return a[1] < b[1];
		});
		int ends = intervals[0][1];//选择终点最小的，作为必选区间
		int ans = 0;
		for (int i = 1; i < n; i++) {
			if (intervals[i][0] < ends) {//产生重叠，不要，因为我们要的是，尽早结束且不重叠区间
				ans++;
			}
			else {
				ends = intervals[i][1];//不重叠，更新终点位置
			}
		}
		return ans;
	}
};