目录
1 简介
2 比例Proportional
3 积分Integral
4 微分Differential
5 公式
6 积分限幅
7 积分限行
8 相关代码
1 简介
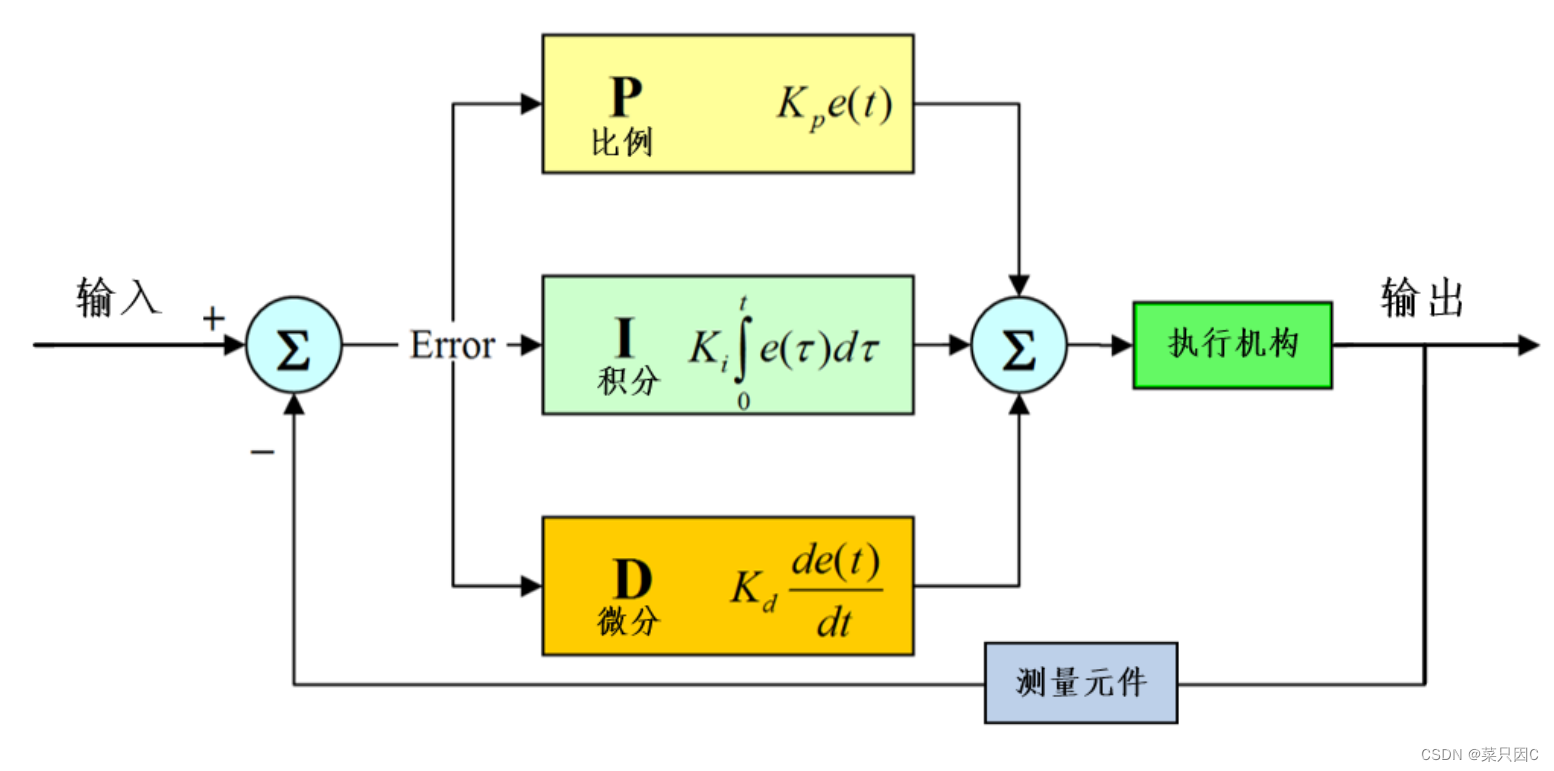
PID控制中有P、I、D三个参数,PID即:Proportional(比例)、Integral(积分)、Differential(微分)的缩写。只有明白这三个参数的含义和作用才能完成控制器PID参数整定,让控制器到达最佳控制效果。
PID是经典的闭环控制算法,具有原理简单,易于实现,适用面广,控制参数相互独立,参数的选定比较简单等优点。
凡是需要将某一个物理量“保持稳定”的场合(比如维持平衡,稳定温度、转速等),PID都会派上大用场。
2 比例Proportional
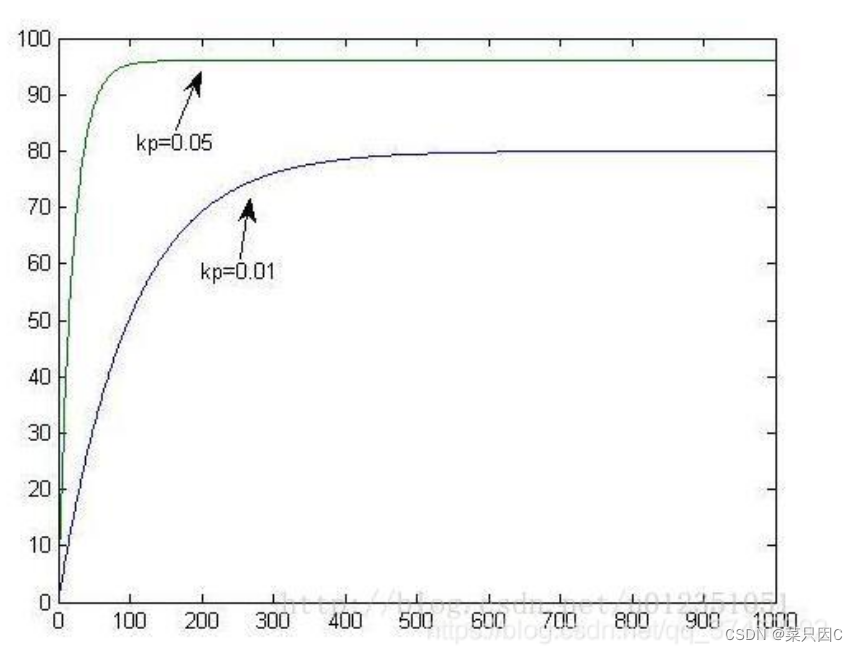
比例控制器实际上就是个放大倍数可调的放大器,即△P=Kp×e,式中Kp为比例增益,即Kp可大于1,也可小于1;e为控制器的输入,也就是测量值与给定值之差,又称为偏差。
比例控制有个缺点,就是会产生余差,要克服余差就必须引入积分作用。
只有比例系数无法准确到达目标位置,但增大比例系数有利于减小误差
3 积分Integral
控制器的积分作用就是为了消除自控系统的余差而设置的。所谓积分,就是随时间进行累积的意思,即当有偏差输入e存在时,积分控制器就要将偏差随时间不断累积起来,也就是积分累积的快慢与偏差e的大小和积分速度成正比。只要有偏差e存在,积分控制器的输出就要改变,也就是说积分总是起作用的,只有偏差不存在时,积分才会停止。
实际上积分作用很少单独使用,通常与比例作用一起使用,使其既具有把偏差放大(或缩小)的比例作用,又具有将偏差随时间累积的积分作用,且其作用方向是一致的。这时控制器的输出为:△P=Ke+△Pi,式中△P为控制器输出值的变化;Ke为比例作用引起的输出;△Pi为积分作用引起的输出。
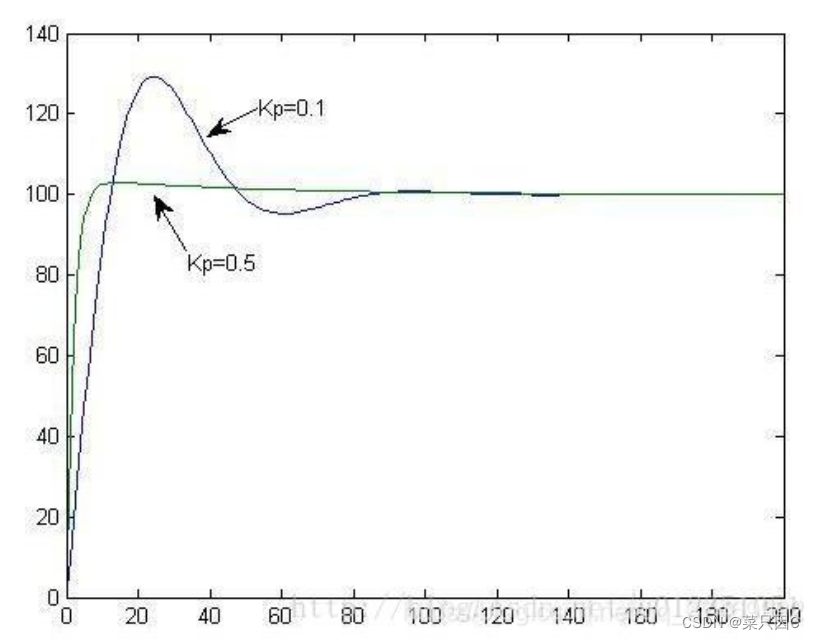
同时使用比例系数和积分可以准确到达目标位置,但当比例系数过大时会出现不稳定性
4 微分Differential
微分作用主要是用来克服被控对象的滞后,常用于温度控制系统。除采用微分作用外,在使用控制系统时要注意测量传送的滞后问题,如温度测量元件的选择和安装位置等。
在常规PID控制器中,微分作用的输出变化与微分时间和偏差变化的速度成比例,而与偏差的大小无关,偏差变化的速度越大,微分时间越长,则微分作用的输出变化越大。但如果微分作用过强,则可能由于变化太快而由其自身引起振荡,使控制器输出中产生明显的“尖峰”或“突跳”。为了避免这一扰动,在PID调节器和DCS中可使用微分先行PID运算规律,即只对测量值PV进行微分,当人工改变控制器的给定值SP时,不会造成控制器输出的突变,避免了改变SP的瞬间给控制系统带来的扰动。如TDC-3000,则在常规PID算法中增加一个软开关,组态时供用户选择控制器对偏差、还是测量值进行微分。
微分保证系统能够平稳运行,不至于出现太大的波动
5 公式
连续形式:
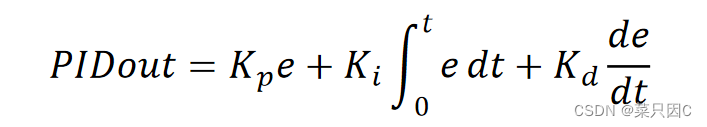
离散形式(常用,由连续形式推导):
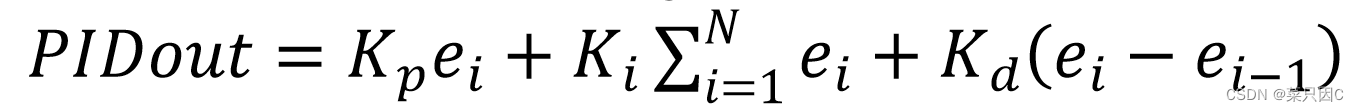
6 积分限幅
试想一下,使用P和I项进行控制,无人机在地面准备起飞,期望高度是100m。此时一个人摁住无人机,那么误差值一直为100m,控制器P项输出保持不变,控制器I项输出是线性增长的
一段时间后,那个人突然不摁了,此时控制器I项输出可能非常大,再加上控制器P项输出,控制器给电机的输出非常大,那么无人机速度就非常快并且飞的非常高。对于这种情况,我们对积分限幅,I项增加到一定值时就不再增了。那么无人机在上面这种情况下就不至于飞的很快很高,这就是积分限幅的作用。
7 积分限行
我们直接将传感器的反馈值分出来一路给到控制器的D项,这样做有一个好处就是如果希望无人机快速反应移动,当期望高度突变的时候,影响会先给到P和I项,由于开始时无人机位置没有突变,传感器反馈的实际高度值也不会突变,因此不会马上给到D项,这样就有效减小了D项开始的缓冲作用,使无人机可以快速反应移动。如果不这样做,那么如果期望高度突变,D项的微分值也会突变变得很大,缓冲作用非常大,使相应效果大大降低。
8 相关代码
chassis_motor_pid[i].SpeedPID.current=motor_chassis[i].speed_rpm;
pid_calc(&chassis_motor_pid[i].SpeedPID);
void pid_calc(_pid* pid)
{
pid->e=pid->target-pid->current;
pid->p_out=(int32_t)(pid->Kp*pid->e);
if(fabs(pid->e)<I_Band)//积分限幅和积分分离
{
pid->i_out+=(int32_t)(pid->Ki*pid->e);
limit(&(pid->i_out),pid->IntegralLimit);
}
else
{
pid->i_out=0;
}
pid->d_out=(int32_t)(pid->Kd*(pid->e-pid->last_e));
pid->total_out=pid->p_out+pid->i_out+pid->d_out;//公式
limit(&(pid->total_out),pid->MaxOutput);//输出限制
pid->last_e=pid->e;//更新last值
}