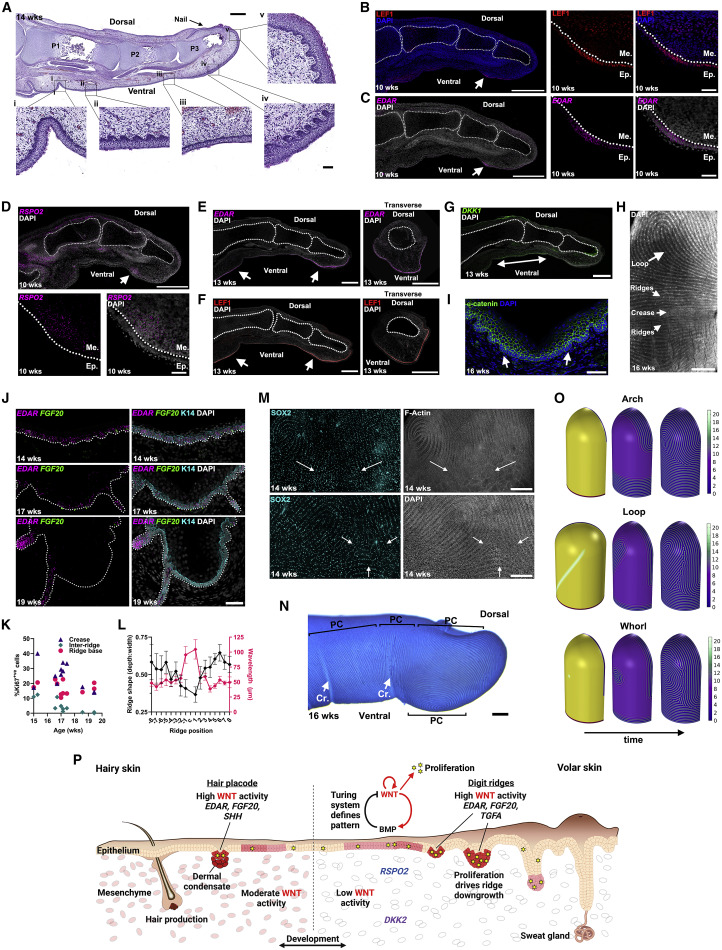
目录
一、性质推导
二、常见的二叉树性质习题
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为()。
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为()。
3.一个具有767个节点的完全二叉树,其叶子节点个数为()。
4.一棵完全二叉树的节点数为531个,那么这棵树的高度为()。
5.在一颗度为3的树中,度为3的结点有2个,度为2的结点有1个,度为1的结点有2个,则叶子结点有( )个。
6.一颗拥有1000个结点的树度为4,则它的最小深度是( )。
7.在一颗完全二叉树中,某一个结点没有其左孩子,则该结点一定( )。
一、性质推导
1. 若一个二叉树有n个节点,则该二叉树共有(n-1)条边。
推导:如图,可以理解为二叉树除了根节点外,每一个节点头上都有一条边指向它。因此,边的总数就是n-1

2. 若规定 根结点的层数为 1 ,则一棵 非空二叉树的第 i 层上最多有 2^(i-1) (i>0) 个结点。
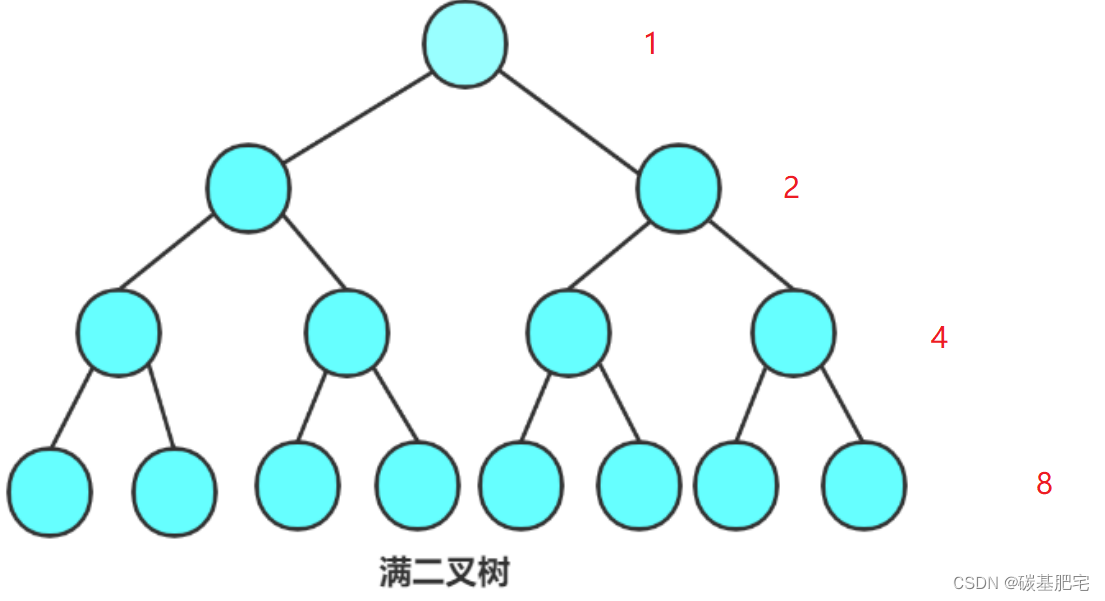
3. 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是 2^k -1
(k>=0)
推导:深度为K的二叉树最大节点的情况是该树为一棵满二叉树。将每一层节点数求和,即该树的总结点数。求和的过程是等比数列的求和过程,根据等比数列求和的公式(其中n是项数):
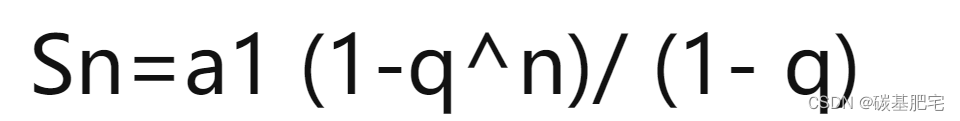
代入a1(首项)为2^0即1,q为2,n为k,可得最大节点数为: 2^k-1
4. 具有 n 个结点的完全二叉树的深度 k为log(n+1)上取整 。
推导:由性质3倒推可得:
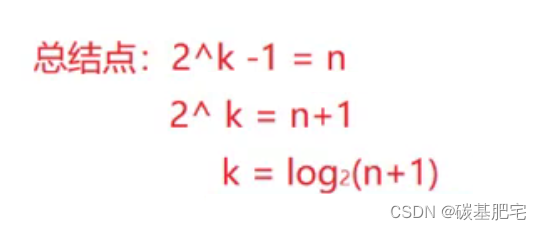
向上取整即若一个数是3点几,则答案向上取4。
假设共有16个节点,n=16.则:2^k = 17,而2^4为16,2^5为32,因此k实际为4点几,但若k取4,则不够,还多了一个节点。因此k应当向上取5.
注意:这里的 k 还有另一种表示方式,即log(n)+1。此时 k 为log(n)+1向下取整。向下取整即3点几向下取3.
5. 对任何一棵二叉树 , 如果其 叶结点个数为 n0, 度为 2 的非叶结点个数为 n2, 则有 n0 = n2 + 1 (度为0的节点个数比度为2的节点个数多一个。)
推导:该结论的推导运用到了二叉树边与节点个数的关系。
假设度为0的节点有n0个,度为1的节点有n1个,度为2的节点有n2个,总结点数为N。首先可得:N = n0 + n1 + n2 ……①(节点个数关系)
同时,由性质1可得,该二叉树有N-1条边。度为0的节点发射出0条边,度为1的节点发射出1条边,度为2的节点发射出2条边。由此可得:
N-1 = 0*n0 + 1*n1 + 2*n2 ……②(边条数关系)
由①和②可得结论:n0 = n2 + 1
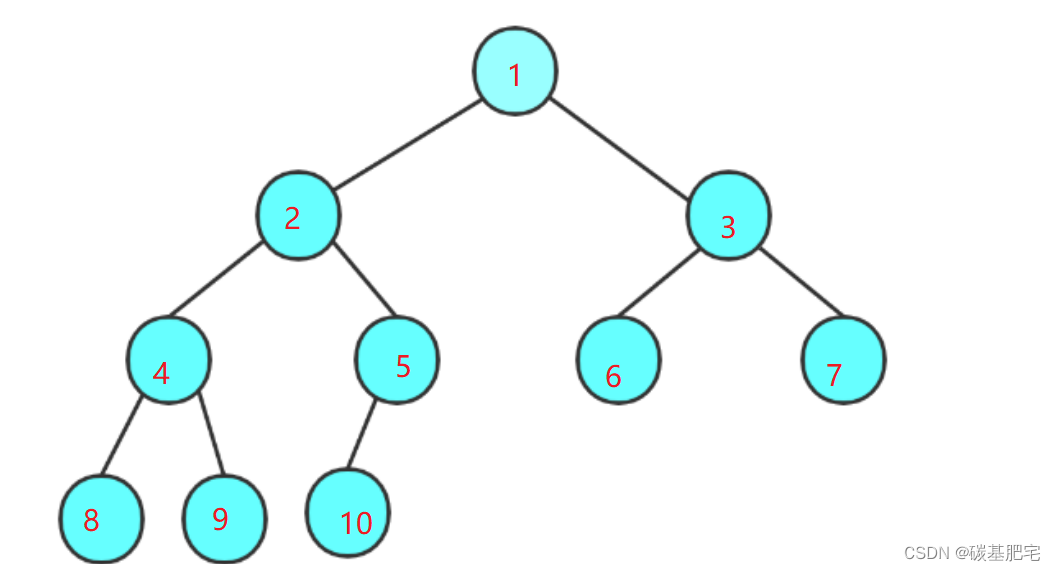
6. 对于具有 n 个结点的完全二叉树 ,如果按照 从上至下从左至右的顺序对所有节点从 0 开始编号 ,则对于 序号为 i 的结点有 :若i>0 ,则其 双亲结点序号为: (i-1)/2 ;若 i=0 , i 为根结点编号 ,无双亲结点。若2i+1<n,则其左孩子序号为: 2i+1; 否则无左孩子。若2i+2<n ,则其右孩子序号: 2i+2; 否则无右孩子。
推导:如下图规律所示。
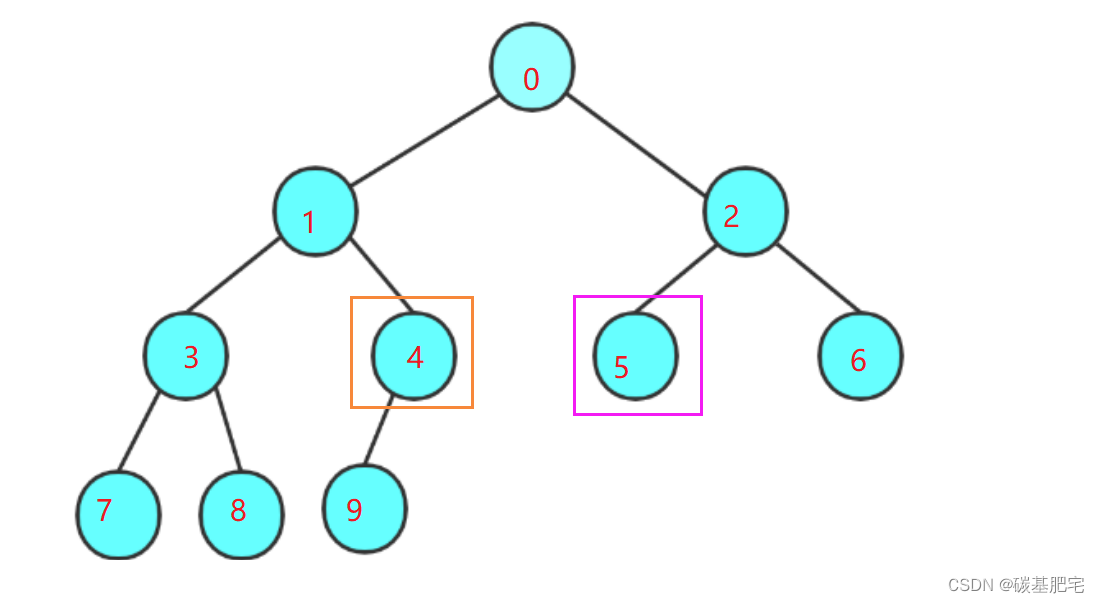
若 i = 4,则其双亲序号为 (i-1)/2 即 (4-1)/2 为1;
左孩子2*i+1为9 < 总结点个数10,因此左孩子存在且序号为9;
右孩子2*i+2为10,不小于10,因此右孩子不存在。
若i = 5,则其双亲序号为(i-1)/2 即 2;
左孩子2*i+1为11大于10,因此左孩子不存在。由于该性质是针对完全二叉树的,因此其右孩子一定也不存在。
注意:若从1开始编号,则序号为i的节点的双亲节点序号为 i/2,左孩子节点为 2*i ,右孩子节点为 2*i + 1.
该结论可以不死记硬背,遇到的时候简单画图即可快速推导。
二、常见的二叉树性质习题
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为()。
A、不存在这样的二叉树
B、200
C、198
D、199
答案选B。
由性质5可知,n0 = n2+1.n0 = 199+1 = 200
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为()。
A n
B n+1
C n-1
D n/2
答案选A。
该题运用到了性质5.
首先分析题干,如何求叶子节点的个数?和节点个数相关的公式有二:
n0 = n2 + 1,N = n0 + n1 + n2
已知总个数N为2n,那么只要知道n1即可求出n0.
这里有一个重要的结论:
在完全二叉树中,如果节点总个数为奇数,则没有度为1的节点;如果节点总个数为偶数,只有一个度为1的节点。

节点个数是偶数,只有一个度为1的节点 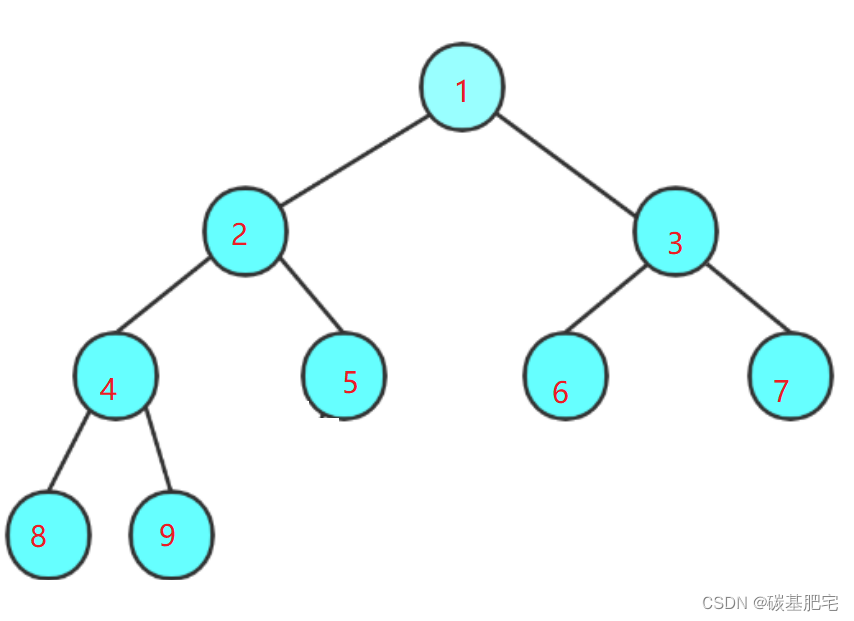
节点个数是奇数,没有度为1的节点 2n为偶数,因此有一个度为1的节点。
2n = n0 + 1 + n2 = n0 + 1 + n0 - 1
2n = 2n0
n0 = n,故选A
3.一个具有767个节点的完全二叉树,其叶子节点个数为()。
A 383
B 384
C 385
D 386
答案选B。
本题同上。此时共有奇数个节点,因此没有度为1的节点,即n1 = 0.
由 N = n0 + n1 + n2得: 767 = n0 + 0 + n0 - 1
n0 = 768/2 = 384
4.一棵完全二叉树的节点数为531个,那么这棵树的高度为()。
A 11
B 10
C 8
D 12
答案选B。
已知节点求高度,运用性质4,h = log(n+1)向上取证。h = log(531+1),向上取整为10,故选B。
5.在一颗度为3的树中,度为3的结点有2个,度为2的结点有1个,度为1的结点有2个,则叶子结点有( )个。
A.4
B.5
C.6
D.7
本题选C。
运用了边与节点个数的关系。
令n3 = 2;n2 = 1;n1 = 2;设总结点的个数为N
则由节点个数的关系得 N = n3 + n2 + n1 + n0,由边条数的关系得 N-1 = 3*n3 + 2*n2 + 1*n1 + 0*n0
联立可得:N = 2 + 1 + 2 + n0,N-1 = 3*2 + 2*1 + 1*2 + 0
n0 = 6
6.一颗拥有1000个结点的树度为4,则它的最小深度是( )。
A.5
B.6
C.7
D.8
答案选B
当这棵树每一层都是满的时,它的深度最小。也就是说,这棵树应当是一棵满四叉树。
假设高度为h,则由求二叉树节点个数的公式类比可知:根据等比数列求和公式得,这个数的节点个数为(4^h - 1) / 3
当h = 5,最大节点数为341,当h = 6, 最大节点数为1365,所以,最小深度应该向上取整为6。
7.在一颗完全二叉树中,某一个结点没有其左孩子,则该结点一定( )。
A.是根结点
B.是叶结点
C.是分支结点
D.在倒数第二层
答案选B.
完全二叉树中,如果一个节点没有左孩子,则一定没有右孩子,它必定为一个叶子节点。
最后一层一定为叶子节点,但是倒数第二层也可能存在叶子节点。
![字母板上的路径[提取公共代码,提高复用率]](https://img-blog.csdnimg.cn/dcdc077c29f14c2cac0d898ace0b53ae.png)