文章目录
- 单组分反应-扩散方程
- 双组分反应-扩散方程
- 三组分和更多组分的反应-扩散方程
- Fisher's equation
- KPP方程
- Belousov–Zhabotinsky reaction
- 历史
- 化学机理
- 变体
- Noise-induced order
- 数学背景
- Briggs–Rauscher reaction
- ZFK equation
- 行波解
- 渐近解
- 外部区域
- 内部区域
- KPP-ZFK 转变
- Clavin–Liñán 模型
- 应用和普遍性
- 指纹的生成
- 独一无二的存在
- 三种重要的信号分子
- 小鼠“指纹”带来的启示
- 时间、位置、形状,都很关键
- 实验
- 数值处理
- 演示工具

反应扩散系统(Reaction–diffusion system)是对应于多种物理现象的数学模型。最常见的是一种或多种化学物质浓度在空间和时间上的变化:物质相互转化的局部化学反应,以及导致物质在空间表面扩散的扩散。
反应扩散系统自然地应用于化学。然而,该系统也可以描述非化学性质的动态过程。例子可以在生物学、地质学和物理学(中子扩散理论)和生态学中找到。在数学上,反应扩散系统采用半线性抛物线偏微分方程(parabolic partial differential equations)的形式。它们可以用一般形式表示
∂ t q = D ‾ ‾ ∇ 2 q + R ( q ) \partial _{t}{\boldsymbol {q}}={\underline {\underline {\boldsymbol {D}}}}\,\nabla ^{2}{\boldsymbol {q}}+{\boldsymbol {R}}({\boldsymbol {q}}) ∂tq=D∇2q+R(q)
其中 q ( x , t ) \bm{q}(\bm{x}, t) q(x,t) 表示未知向量函数, D ‾ ‾ \underline {\underline {\boldsymbol {D}}} D 是扩散系数(diffusion coefficients)的对角矩阵, R \bm{R} R 表示所有局部反应。反应扩散方程的解表现出广泛的行为,包括行波和类波现象的形成,以及其他自组织模式,如条纹、六边形或更复杂的结构,如耗散孤子。这种模式被称为“图灵模式(Turing patterns)”。反应-扩散微分方程成立的每个函数实际上代表一个浓度变量。
单组分反应-扩散方程
最简单的反应扩散方程是在平面几何中的一个空间维度上,
∂ t u = D ∂ x 2 u + R ( u ) \partial _{t}u=D\partial _{x}^{2}u+R(u) ∂tu=D∂x2u+R(u)
也称为 Kolmogorov–Petrovsky–Piskunov equation。如果反应项消失,则方程表示纯扩散过程。对应的方程是菲克第二定律(Fick’s second law)。选择 R ( u ) = u ( 1 − u ) R(u) = u(1 − u) R(u)=u(1−u) 产生最初用于描述生物种群扩散的 Fisher’s equation 。Newell-Whitehead-Segel 方程 R ( u ) = u ( 1 − u 2 ) R(u) = u(1 − u^{2}) R(u)=u(1−u2) 为了描述 Rayleigh–Bénard 对流,更一般的 Zeldovich–Frank-Kamenetskii equation R ( u ) = u ( 1 − u ) e − β ( 1 − u ) R(u) = u(1 − u)e^{-\beta(1-u)} R(u)=u(1−u)e−β(1−u) 和 0 < β < ∞ 0 < \beta < \infty 0<β<∞(Zeldovich number)出现在燃烧理论中,及其 R ( u ) = u 2 − u 3 R(u) = u^{2} − u^{3} R(u)=u2−u3 的特定退化情况,有时也称为 Zeldovich 方程。
单组分系统的动力学受到一定的限制,因为演化方程也可以写成变分形式
∂ t u = − δ L δ u \partial _{t}u=-{\frac {\delta {\mathfrak {L}}}{\delta u}} ∂tu=−δuδL
因此描述了“自由能”的永久减少 L \mathfrak {L} L 由泛函给出
L = ∫ − ∞ ∞ [ D 2 ( ∂ x u ) 2 − V ( u ) ] d x {\displaystyle {\mathfrak {L}}=\int _{-\infty }^{\infty }\left[{\tfrac {D}{2}}\left(\partial _{x}u\right) ^{2}-V(u)\right]\,{\text{d}}x} L=∫−∞∞[2D(∂xu)2−V(u)]dx
其中势能 V ( u ) V(u) V(u) 可以有例如 R ( u ) = d V ( u ) d u R(u) = \frac{\mathrm{d}V(u)}{\mathrm{d}u} R(u)=dudV(u) 的形式。

在具有多个稳态齐次解的系统中,典型的解是通过连接齐次状态的行进前沿给出的。这些解在不改变形状的情况下以恒定速度移动,并且具有
u
(
x
,
t
)
=
u
^
(
ξ
)
u(x, t) = \hat{u}(\xi)
u(x,t)=u^(ξ) 和
ξ
=
x
−
c
t
\xi = x − ct
ξ=x−ct 的形式,其中
c
c
c 是行波的速度。请注意,虽然行波通常是稳定的结构,但所有非单调稳态解(例如,由前-反前对(front-antifront pair)组成的局部域)都是不稳定的。对于
c
=
0
c = 0
c=0,此陈述有一个简单的证明:如果
u
0
(
x
)
u_{0}(x)
u0(x) 是平稳解且
u
=
u
0
(
x
)
+
u
~
(
x
,
t
)
u = u_{0}(x) + \tilde{u}(x, t)
u=u0(x)+u~(x,t) 是无限微扰动解,则线性稳定性分析会得出方程式:
∂ t u ~ = D ∂ x 2 u ~ − U ( x ) u ~ , U ( x ) = − R ′ ( u ) ∣ u = u 0 ( x ) {\displaystyle \partial _{t}{\tilde {u}}=D\partial _{x}^{2}{\tilde {u}}-U(x){\tilde {u}},\qquad U(x)=-R^{\prime }(u){\Big |}_{u=u_{0}(x)}} ∂tu~=D∂x2u~−U(x)u~,U(x)=−R′(u) u=u0(x)
通过假设 u ~ = ψ ( x ) exp ( − λ t ) \tilde{u}= \psi(x)\exp(−\lambda t) u~=ψ(x)exp(−λt) 我们得到了特征值问题:
H ^ ψ = λ ψ , H ^ = − D ∂ x 2 + U ( x ) {\hat {H}}\psi =\lambda \psi ,\qquad {\hat {H}}=-D\partial _{x}^{2}+U(x) H^ψ=λψ,H^=−D∂x2+U(x)
Schrödinger type,其中负特征值导致解的不稳定性。由于平移不变性, ψ = ∂ x u 0 ( x ) \psi =\partial_{x} u_{0}(x) ψ=∂xu0(x) 是特征值 λ = 0 \lambda = 0 λ=0 的中性特征函数,所有其他特征函数都可以根据节点数量的增加进行排序,相应的实特征值的大小随 0 的数量单调增加。特征函数 ψ = ∂ x u 0 ( x ) \psi =\partial_{x} u_{0}(x) ψ=∂xu0(x) 应该至少有一个零,对于非单调平稳解,相应的特征值 λ = 0 \lambda = 0 λ=0 不可能是最低的,因此意味着不稳定性。
要确定移动前沿的速度 c c c,可以转到移动坐标系并查看稳态解:
D ∂ ξ 2 u ^ ( ξ ) + c ∂ ξ u ^ ( ξ ) + R ( u ^ ( ξ ) ) = 0 D\partial _{\xi }^{2}{\hat {u}}(\xi )+c\partial _{\xi }{\hat {u}}(\xi )+R({\hat { u}}(\xi))=0 D∂ξ2u^(ξ)+c∂ξu^(ξ)+R(u^(ξ))=0
这个方程有一个很好的机械类比,在阻尼系数为 c c c 的力 R R R 下,一个位置为 u ^ \hat{u} u^ 的质量 D D D 在“时间” ξ \xi ξ 过程中的运动,这让我们有了一个很好的说明方法来构造不同类型的解和确定 c c c。
当从一个空间维度转向多个空间维度时,仍然可以应用来自一维系统的许多陈述。平面或弯曲的波阵面是典型的结构,随着弯曲波阵面的局部速度变得取决于局部曲率半径(这可以通过转到极坐标可以看出),会出现一种新的效果。这种现象导致了所谓的曲率驱动的不稳定性。
双组分反应-扩散方程
双组分系统比单组分系统允许更大范围的可能现象。艾伦·图灵首先提出的一个重要想法是,在局部系统中稳定的状态在存在扩散的情况下可能变得不稳定。
然而,线性稳定性分析表明,当对一般的双组分系统进行线性化时:
( ∂ t u ∂ t v ) = ( D u 0 0 D v ) ( ∂ x x u ∂ x x v ) + ( F ( u , v ) G ( u , v ) ) {\displaystyle {\begin{pmatrix}\partial _{t}u\\\partial _{t}v\end{pmatrix}}={\begin{pmatrix}D_{u}&0\\0&D_{v}\end{pmatrix}}{\begin{pmatrix}\partial _{xx}u\\\partial _{xx}v\end{pmatrix}}+{\begin{pmatrix}F(u,v)\\G(u,v)\end{pmatrix}}} (∂tu∂tv)=(Du00Dv)(∂xxu∂xxv)+(F(u,v)G(u,v))
平面波扰动
q ~ k ( x , t ) = ( u ~ ( t ) v ~ ( t ) ) e i k ⋅ x {\tilde {\boldsymbol {q}}}_{\boldsymbol {k}}({\boldsymbol {x}},t)={\begin{pmatrix}{\tilde {u}}(t)\\{ \tilde {v}}(t)\end{pmatrix}}e^{i{\boldsymbol {k}}\cdot {\boldsymbol {x}}} q~k(x,t)=(u~(t)v~(t))eik⋅x
的稳态齐次解将满足
( ∂ t u ~ k ( t ) ∂ t v ~ k ( t ) ) = − k 2 ( D u u ~ k ( t ) D v v ~ k ( t ) ) + R ′ ( u ~ k ( t ) v ~ k ( t ) ) {\begin{pmatrix}\partial _{t}{\tilde {u}}_{\boldsymbol {k}}(t)\\\partial _{t}{\tilde {v}}_{\boldsymbol { k}}(t)\end{pmatrix}}=-k^{2}{\begin{pmatrix}D_{u}{\tilde {u}}_{\boldsymbol {k}}(t)\\D_ {v}{\tilde {v}}_{\boldsymbol {k}}(t)\end{pmatrix}}+{\boldsymbol {R}}^{\prime }{\begin{pmatrix}{\tilde { u}}_{\boldsymbol {k}}(t)\\{\tilde {v}}_{\boldsymbol {k}}(t)\end{pmatrix}} (∂tu~k(t)∂tv~k(t))=−k2(Duu~k(t)Dvv~k(t))+R′(u~k(t)v~k(t))
图灵的想法只能在以反应函数的雅可比矩阵 R ′ R' R′ 的符号表征的四个等价类系统中实现。特别地,如果有限波矢 k k k 被认为是最不稳定的波矢,则雅可比行列式必须具有符号
( + − + − ) , ( + + − − ) , ( − + − + ) , ( − − + + ) {\begin{pmatrix}+&-\\+&-\end{pmatrix}},\quad {\begin{pmatrix}+&+\\-&-\end{pmatrix}},\quad {\begin{pmatrix}-&+\\-&+\end{pmatrix}},\quad {\begin{pmatrix}-&-\\+&+\end{pmatrix}} (++−−),(+−+−),(−−++),(−+−+)
此类系统以其第一个代表命名为激活剂-抑制剂系统(activator-inhibitor system):接近基态时,一种成分刺激两种成分的产生,而另一种成分抑制它们的生长。其最突出的代表是 FitzHugh-Nagumo equation:
∂ t u = d u 2 ∇ 2 u + f ( u ) − σ v , τ ∂ t v = d v 2 ∇ 2 v + u − v {\begin{aligned}\partial _{t}u&=d_{u}^{2}\,\nabla ^{2}u+f(u)-\sigma v,\\\tau \partial _{t }v&=d_{v}^{2}\,\nabla ^{2}v+u-v\end{aligned}} ∂tuτ∂tv=du2∇2u+f(u)−σv,=dv2∇2v+u−v
其中 f ( u ) = λ u − u 3 − κ f (u) = λu − u^{3} − \kappa f (u)=λu−u3−κ 描述了动作电位如何通过神经传播。这里, d u d_{u} du、 d v d_{v} dv、 τ \tau τ、 σ \sigma σ 和 λ \lambda λ 是正常数。
当激活剂-抑制剂系统经历参数变化时,可能会从均匀基态稳定的条件转变为线性不稳定的条件。相应的分岔可以是到具有主导波数 k = 0 k = 0 k=0 的全局振荡均匀(homogeneous)状态的 Hopf bifurcation,或者是到具有主导有限波数的全局图案化状态的图灵分岔(Turing bifurcation)。后者在两个空间维度上通常会导致条纹或六边形图案。
- 亚临界图灵分岔(Subcritical Turing bifurcation):在上述 Fitzhugh-Nagumo 型双组分反应扩散系统中,从嘈杂的初始条件形成六边形图案。



对于 Fitzhugh–Nagumo 示例,标记 Turing 和 Hopf 分岔线性稳定区域边界的中性稳定性曲线(neutral stability curves)由下式给出:
q n H ( k ) : 1 τ + ( d u 2 + 1 τ d v 2 ) k 2 = f ′ ( u h ) , q n T ( k ) : κ 1 + d v 2 k 2 + d u 2 k 2 = f ′ ( u h ) . {\begin{aligned}q_{\text{n}}^{H}(k):&{}\quad {\frac {1}{\tau }}+\left(d_{u}^{2} +{\frac {1}{\tau }}d_{v}^{2}\right)k^{2}&=f^{\prime }(u_{h}),\\[6pt]q_{ \text{n}}^{T}(k):&{}\quad {\frac {\kappa }{1+d_{v}^{2}k^{2}}}+d_{u}^ {2}k^{2}&=f^{\prime }(u_{h}).\end{aligned}} qnH(k):qnT(k):τ1+(du2+τ1dv2)k21+dv2k2κ+du2k2=f′(uh),=f′(uh).
如果分叉是亚临界的,通常可以在斑图与基态共存的滞回区域(hysteretic region)中观察到局部结构(耗散孤子(dissipative solitons))。其他经常遇到的结构包括脉冲序列(也称为周期性行波(periodic travelling waves))、螺旋波(spiral waves)和目标斑图(target patterns)。这三种解类型也是双(或多)组分反应-扩散方程的一般特征,其中局部动力学具有稳定的极限环。
在上述 Fitzhugh-Nagumo 型双组分反应-扩散系统中发现的其他模式。



三组分和更多组分的反应-扩散方程
对于各种系统,已经提出了具有两个以上组分的反应-扩散方程,例如 Belousov–Zhabotinsky reaction,用于凝血(blood clotting),裂变波(fission waves)或平面气体放电系统(planar gas discharge systems)。
众所周知,具有更多组分的系统允许出现在具有一个或两个组件的系统中不可能出现的各种现象(例如,在没有全局反馈的情况下在多个空间维度上稳定运行脉冲)。
Fisher’s equation

在数学中,Fisher 方程(以统计学家和生物学家 Ronald Fisher 的名字命名)也称为 Kolmogorov–Petrovsky–Piskunov 方程(以 Andrey Kolmogorov、Ivan Petrovsky 和 Nikolai Piskunov 的名字命名)、KPP 方程或 Fisher–KPP 方程,这是一种偏微分方程 :
∂ u ∂ t − D ∂ 2 u ∂ x 2 = r u ( 1 − u ) {\displaystyle {\frac {\partial u}{\partial t}}-D{\frac {\partial ^{2}u}{\partial x^{2}}}=ru(1-u)} ∂t∂u−D∂x2∂2u=ru(1−u)
它是一种反应扩散系统,可用于模拟种群增长和波传播。
Fisher 方程属于反应-扩散方程类:实际上,它是最简单的半线性反应-扩散方程之一,具有非齐次项:
f ( u , x , t ) = r u ( 1 − u ) {\displaystyle f(u,x,t)=ru(1-u)} f(u,x,t)=ru(1−u)
它可以展示在由下式给出的平衡状态之间切换的行波解 f ( u ) = 0 f(u)=0 f(u)=0。此类方程出现在例如生态学、生理学、燃烧、结晶、等离子体物理学和一般相变问题中。
Fisher 在他 1937 年的论文 “The wave of advance of advanced genes in the context of population dynamics” 中提出了这个方程来描述优势等位基因的空间分布,并探索了它的行波解。对于每个波速 c ≥ 2 r D c\geq 2{\sqrt {rD}} c≥2rD(无量纲下为 c ≥ 2 c\geq 2 c≥2),它允许下面形式的行波解:
u ( x , t ) = v ( x ± c t ) ≡ v ( z ) u(x,t)=v(x\pm ct)\equiv v(z) u(x,t)=v(x±ct)≡v(z)
其中 v \textstyle{v} v 正在增加并且
lim z → − ∞ v ( z ) = 0 , lim z → ∞ v ( z ) = 1 \lim _{{z\rightarrow -\infty }}v\left(z\right)=0,\quad \lim _{{z\rightarrow \infty }}v\left(z\right)=1 z→−∞limv(z)=0,z→∞limv(z)=1
也就是说,解从平衡状态 u = 0 u = 0 u=0 切换到平衡状态 u = 1 u = 1 u=1。对于 c < 2 c < 2 c<2,不存在这样的解。给定波速的波形是唯一的。行波解对近场扰动是稳定的,但对会加厚尾部的远场扰动则不稳定。用比较原理(comparison principle)和超解理论(super-solution theory)可以证明,所有具有紧致(compact)初始数据的解都以最小速度收敛于波。
对于特殊的波速 c = ± 5 / 6 c=\pm 5/{\sqrt {6}} c=±5/6,所有的解都可以在一个封闭的形式中找到:
v ( z ) = ( 1 + C e x p ( ∓ z / 6 ) ) − 2 {\displaystyle v(z)=\left(1+C\mathrm {exp} \left(\mp {z}/{\sqrt {6}}\right)\right)^{-2}} v(z)=(1+Cexp(∓z/6))−2
其中 C C C 任意,满足上述极限条件为 C > 0 C>0 C>0。
行波解存在性的证明及其性质的分析通常通过相空间方法(phase space method)来完成。
KPP方程
同年(1937)Fisher、Kolmogorov、Petrovsky 和 Piskunov 引入了更一般的反应-扩散方程:
∂ u ∂ t − ∂ 2 u ∂ x 2 = F ( u ) {\displaystyle {\frac {\partial u}{\partial t}}-{\frac {\partial ^{2}u}{\partial x^{2}}}=F(u)} ∂t∂u−∂x2∂2u=F(u)
其中 F F F 是一个足够光滑的函数,具有以下属性: F ( 0 ) = F ( 1 ) = 0 , F ′ ( 0 ) = r > 0 F(0)=F(1)=0,F'(0)=r>0 F(0)=F(1)=0,F′(0)=r>0 和 F ( v ) > 0 , F ′ ( v ) < r F(v)>0,F'(v)<r F(v)>0,F′(v)<r 对于所有 0 < v < 1 0<v<1 0<v<1。这也有上面讨论的行波解决方案。通过假定 F ( u ) = r u ( 1 − u ) F(u)=ru(1-u) F(u)=ru(1−u) 并重新缩放 x x x 坐标系数 D \sqrt {D} D,我们可以得到 Fisher 方程。 一个更一般的例子是:
F ( u ) = r u ( 1 − u q ) , q > 0 {\displaystyle F(u)=ru(1-u^{q})},q>0 F(u)=ru(1−uq),q>0
Kolmogorov、Petrovsky 和 Piskunov 讨论了在种群遗传学的背景下 q = 2 q=2 q=2 的例子。
KPP 型行波的最小速度为:
2 d F d u ∣ u = 0 {\displaystyle 2{\sqrt {\left.{\frac {dF}{du}}\right|_{u=0}}}} 2dudF u=0
这不同于其他类型的波,例如 ZFK-type waves。
Belousov–Zhabotinsky reaction
Belousov–Zhabotinsky 反应或 BZ 反应是作为非平衡热力学经典例子的一类反应之一,导致非线性化学振荡器的建立。 这些振荡器中唯一的共同元素是溴和酸。

这些反应对理论化学很重要,因为它们表明化学反应不必受平衡热力学行为的支配。这些反应远未达到平衡,并且会在很长一段时间内保持这种状态,并且会混乱地演变。从这个意义上说,它们提供了一个有趣的非平衡生物现象的化学模型;因此,BZ 反应本身的数学模型和模拟具有理论意义,如噪声诱导有序。

BZ 反应的一个重要方面是它所谓的“激发性(excitability)”;在刺激的影响下,模式在原本完全静止的介质中发展。一些时钟反应,例如 Briggs–Rauscher 和 BZ,使用tris(bipyridine)ruthenium(II) chloride 作为催化剂,可以通过光的影响激发自组织活动。
历史

这一现象的发现归功于 Boris Belousov。1951 年,在试图寻找 Krebs cycle 的非有机类似物时,他注意到在稀硫酸中溴酸钾、硫酸铈 (IV)、丙二酸和柠檬酸的混合物中, 铈 (IV) 和铈 (III) 离子发生振荡,导致溶液颜色在黄色溶液和无色溶液之间振荡。这是因为铈 (IV) 离子被丙二酸还原为铈 (III) 离子,然后又被溴酸盐 (V) 离子氧化回铈 (IV) 离子。
Belousov 曾两次尝试发表他的发现,但都被拒绝了,理由是他无法解释他的结果以使他提交结果的期刊编辑满意。苏联生物化学家 Simon El’evich Shnoll 鼓励 Belousov 继续努力发表他的成果。1959 年,他的作品终于发表在一份不太受人尊敬的未经审查的期刊上。
Belousov 发表后,Shnoll 于 1961 年将该项目交给了研究生 Anatol Zhabotinsky,后者详细研究了反应序列;然而,这些人的工作成果仍未得到广泛传播,在西方也不为人所知,直到 1968 年在布拉格举行的一次会议。
在化学文献和网络上可以找到许多 BZ 混合物。 铁蛋白(Ferroin)是一种菲咯啉(phenanthroline)和铁的复合物,是一种常见的指示剂。如果在培养皿中进行这些反应,则首先会形成彩色斑点。这些点长成一系列扩展的同心环或可能扩展的螺旋,类似于循环元胞自动机生成的模式。如果摇动盘子,颜色会消失,然后重新出现。波一直持续到试剂被消耗完。该反应也可以在使用磁力搅拌器的烧杯中进行。
Andrew Adamatzky,西英格兰大学的计算机科学家,报告了使用 BZ 反应的液体逻辑门(liquid logic gates)。BZ 反应也被 Juan Pérez-Mercader 和他在哈佛大学的团队用来创建一个完全化学的图灵机,能够识别乔姆斯基类型 1 语言。
惊人相似的振荡螺旋模式出现在自然界的其他地方,在非常不同的空间和时间尺度上,例如盘基网柄菌的生长模式,一种土壤栖息的变形虫菌落。在 BZ 反应中,相互作用元素的大小是分子大小,反应的时间尺度是分钟。就土壤变形虫而言,元素的大小是单细胞生物的典型特征,所涉及的时间在几天到几年的数量级。
研究人员还在探索创建“湿式计算机(wet computer)”,使用自我创建的“细胞”和其他技术来模仿神经元的某些特性。
化学机理
这种反应的机制非常复杂,被认为涉及大约 18 个不同的步骤,这些步骤已成为许多研究论文的主题。
以类似于 Briggs–Rauscher 反应的方式,发生两个关键过程(两者都是自催化的);过程 A 生成分子溴,呈现红色,过程 B 消耗溴生成溴离子。从理论上讲,该反应类似于理想的图灵模式,该系统通过求解产生反应抑制剂和反应促进剂的反应的反应扩散方程定性地出现,其中两者以不同的速率在介质中扩散。
该反应最常见的变化之一是使用丙二酸 (CH2(CO2H)2) 作为酸,使用溴酸钾 (KBrO3) 作为溴源。 总方程为:
3 C H 2 ( C O 2 H ) 2 + 4 B r O 3 − → 4 B r − + 9 C O 2 + 6 H 2 O \mathrm{3 CH_{2}(CO_{2}H)_{2} + 4 BrO^{−}_{3} \rightarrow 4 Br^{−} + 9 CO_{2} + 6 H_{2}O} 3CH2(CO2H)2+4BrO3−→4Br−+9CO2+6H2O
变体
存在许多反应变体。唯一的关键化学品是溴酸盐氧化剂。催化剂离子通常是铈,但也可以是锰,或铁、钌、钴、铜、铬、银、镍和锇的络合物。 可以使用许多不同的还原剂。 (Zhabotinsky, 1964b; Field and Burger, 1985)
当反应在微乳液(microemulsion)中运行时,可以观察到许多不同的模式。
Noise-induced order
噪声诱导有序(Noise-induced order)是 Belosov-Zhabotinski 反应的 Matsumoto-Tsuda 模型中出现的一种数学现象。
在这个模型中,向系统添加噪声会导致从“混乱”行为转变为更“有序”的行为;这篇文章是该领域的开创性论文,产生了大量引用,并催生了应用数学和物理学的一系列研究。这种现象后来在 Belosov-Zhabotinsky 反应中被观察到。
数学背景
从 Belosouv-Zabotinsky 反应中插入实验数据,Matsumoto 和 Tsuda 引入了一个一维模型,一个具有均匀加性噪声的随机动力系统,由映射驱动:
T ( x ) = { ( a + ( x − 1 8 ) 1 3 ) e − x + b , 0 ≤ x ≤ 0.3 c ( 10 x e − 10 x 3 ) 19 + b 0.3 ≤ x ≤ 1 {\displaystyle T(x)={\begin{cases}(a+(x-{\frac {1}{8}})^{\frac {1}{3}})e^{-x}+b ,&0\leq x\leq 0.3\\c(10xe^{\frac {-10x}{3}})^{19}+b&0.3\leq x\leq 1\end{cases}}} T(x)={(a+(x−81)31)e−x+b,c(10xe3−10x)19+b0≤x≤0.30.3≤x≤1
其中:
- a = 19 42 ⋅ ( 7 5 ) 1 / 3 a={\frac {19}{42}}\cdot {\bigg (}{\frac {7}{5}}{\bigg )}^{1/3} a=4219⋅(57)1/3 (定义为 T ′ ( 0. 3 − ) = 0 T'(0.3^{-})=0 T′(0.3−)=0),
- b = 0.0232885283030703205447815804402391873566994364808885264612318273983102252 8 158 213 b=0.02328852830307032054478158044023918735669943648088852646123182739831022528_{158}^{213} b=0.02328852830307032054478158044023918735669943648088852646123182739831022528158213,使得 T 5 ( 0.3 ) T^{5}(0.3) T5(0.3) 落在一个排斥不动点上(在某种程度上这类似于 Misiurewicz point)
- c = 20 3 20 ⋅ 7 ⋅ ( 7 5 ) 1 / 3 ⋅ e 187 / 10 c={\frac {20}{3^{20}\cdot 7}}\cdot {\bigg (}{\frac {7}{5}}{\bigg )}^{1/3} \cdot e^{187/10} c=320⋅720⋅(57)1/3⋅e187/10(定义为 T ( 0. 3 − ) = T ( 0. 3 + ) T(0.3^{-})=T(0.3^{+}) T(0.3−)=T(0.3+))。
使用浮点算法模拟具有不同噪声振幅的随机动力系统,并计算模拟轨道上的李雅普诺夫指数; 随着噪声幅度的增加,这个模拟系统的 Lyapunov 指数被发现从正向负转变。
浮点系统和原始系统的行为可能不同;因此,这不是该现象的严格数学证明。
2017 年给出了具有上述参数的 Matsumoto-Tsuda 映射的噪声诱导有序的计算机辅助证明。在 2020 年,一维映射给出了噪声诱导有序的充分条件:小噪声情况下,Lyapunov 指数为正,而关于勒贝格函数(Lebesgue)的导数的对数平均值为负。
Briggs–Rauscher reaction
wiki: Briggs–Rauscher reaction
ZFK equation
ZFK 方程是 Zeldovich–Frank-Kamenetskii 方程的缩写,是模拟预混火焰传播(premixed flame propagation)的反应扩散方程。该方程以 Yakov Zeldovich 和 David A. Frank-Kamenetskii 的名字命名,他们于 1938 年推导出该方程,也称为 Nagumo 方程。该方程类似于 KPP 方程,只是它包含反应项的指数行为,并且在行波的传播速度方面与 KPP 方程有根本的不同。在无量纲形式中,等式为:
∂ θ ∂ t = ∂ 2 θ ∂ x 2 + ω ( θ ) {\displaystyle {\frac {\partial \theta }{\partial t}}={\frac {\partial ^{2}\theta }{\partial x^{2}}}+\omega (\theta )} ∂t∂θ=∂x2∂2θ+ω(θ)
ω \omega ω 有一个典型的形式:
ω = β 2 2 θ ( 1 − θ ) e − β ( 1 − θ ) {\displaystyle \omega ={\frac {\beta ^{2}}{2}}\theta (1-\theta )e^{-\beta (1-\theta )}} ω=2β2θ(1−θ)e−β(1−θ)
其中 θ ∈ [ 0 , 1 ] \theta \in [0,1] θ∈[0,1] 是无量纲因变量(通常是温度), β \beta β 是 Zeldovich number。 在 ZFK 机制(ZFK regime)下, β ≫ 1 \beta \gg 1 β≫1。 该方程式简化为 Fisher 方程式 β ≪ 1 \beta \ll 1 β≪1。因此 β ≪ 1 \beta \ll 1 β≪1 对应于 KPP 机制。ZFK 机制中行波的最小传播速度 U m i n U_{\mathrm{min}} Umin (通常是长时间渐近速度),由下式给出:
U Z F K ∝ 2 ∫ 0 1 ω ( θ ) d θ {\displaystyle U_{ZFK}\propto {\sqrt {2\int _{0}^{1}\omega (\theta )d\theta }}} UZFK∝2∫01ω(θ)dθ
而在 KPP 机制中,它由
U K P P = 2 d ω d θ ∣ θ = 0 . {\displaystyle U_{KPP}=2{\sqrt {\left.{\frac {d\omega }{d\theta }}\right|_{\theta =0}}}.} UKPP=2dθdω θ=0.
行波解

与 Fisher 方程类似,可以找到该问题的行波解。假设波以恒定速度
U
U
U 从右向左传播,波的坐标中,即
z
=
x
+
U
t
z=x+Ut
z=x+Ut,问题变得稳定。ZFK 方程简化为:
U d θ d z = d 2 θ d z 2 + β 2 2 θ ( 1 − θ ) e − β ( 1 − θ ) {\displaystyle U{\frac {\mathrm{d}\theta }{\mathrm{d}z}}={\frac {\mathrm{d}^{2}\theta }{\mathrm{d}z^{2}}}+{\frac {\beta ^{2}}{ 2}}\theta (1-\theta )e^{-\beta (1-\theta )}} Udzdθ=dz2d2θ+2β2θ(1−θ)e−β(1−θ)
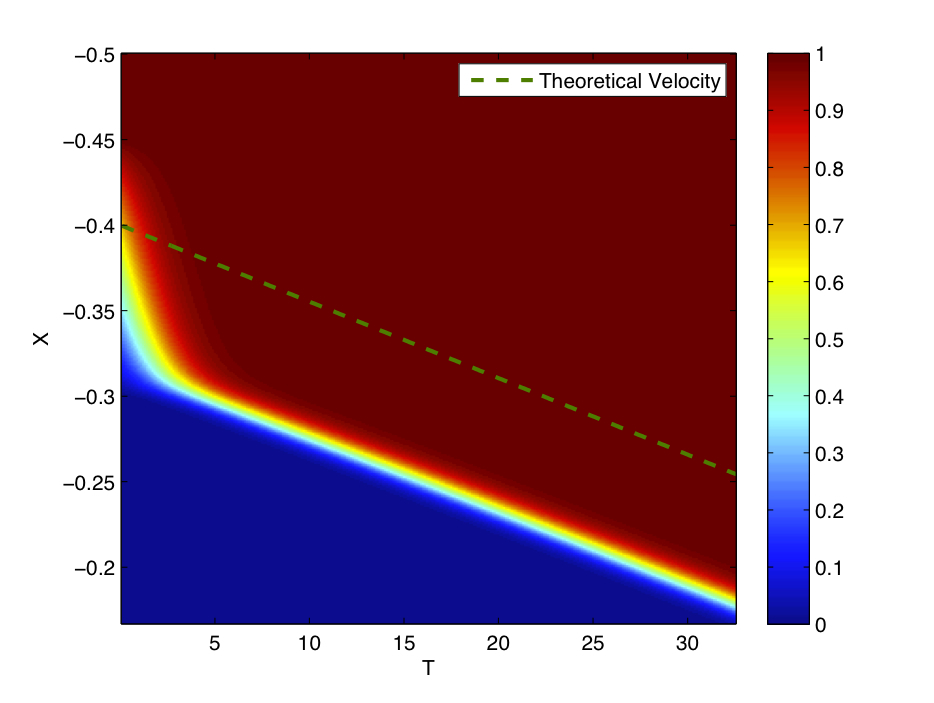
满足边界条件 θ ( − ∞ ) = 0 \theta (-\infty )=0 θ(−∞)=0 和 θ ( ∞ ) = 1 \theta (\infty )=1 θ(∞)=1。边界条件足够平滑,使得导数 d θ / d z d\theta /dz dθ/dz 消失,即 z → ± ∞ z\rightarrow \pm \infty z→±∞。 由于方程在 z z z 方向上是平移不变的,因此可以使用一个附加条件,例如 θ ( 0 ) = 1 / 2 \theta(0)=1/2 θ(0)=1/2 来确定波的位置。波速 U U U 作为解的一部分得到,从而构成一个非线性特征值问题。上述方程的数值解, θ \theta θ,特征值 U U U 和相应的反应项 ω \omega ω 如图所示,其中 β = 15 \beta =15 β=15。
渐近解
当 β → ∞ \beta\rightarrow\infty β→∞ 时,ZFK 机制使用活化能渐近法(activation energy asymptotics)进行正式分析。由于 β \beta β 很大, e − β ( 1 − θ ) e^{-\beta (1-\theta )} e−β(1−θ) 将使反应项几乎为零,但是如果 1 − θ ∼ 1 / β 1-\theta \sim 1/\beta 1−θ∼1/β,在其不可忽略。当 θ = 0 \theta =0 θ=0 或 θ = 1 \theta=1 θ=1 时,反应项也将消失。因此,很明显 ω \omega ω 除了靠近右边界 θ = 1 \theta=1 θ=1 的薄层外,在任何地方都可以忽略不计。因此,问题被分成三个区域,一个内部扩散-反应区域,两侧是两个外部对流-扩散区域(convective-diffusive regions)。
外部区域
外部区域的问题由下式给出:
U d θ d z = d 2 θ d z 2 {\displaystyle U{\frac {\mathrm{d}\theta }{\mathrm{d}z}}={\frac {\mathrm{d}^{2}\theta }{\mathrm{d}z^{2}}}} Udzdθ=dz2d2θ
满足条件 θ ( − ∞ ) = 0 \theta (-\infty )=0 θ(−∞)=0 的解是 θ = e U z \theta =e^{Uz} θ=eUz。这个解也是为了满足 θ ( 0 ) = 1 \theta(0)=1 θ(0)=1(任意选择)来固定波在定义域中的某个位置,因为问题在 z z z 方向上是平移不变的。当 z → 0 − z\rightarrow 0^{-} z→0−,外部解(outer solution)的行为就像 θ = 1 + U z + ⋯ \theta =1+Uz+\cdots θ=1+Uz+⋯,这反过来意味着 d θ / d z = U + ⋯ \mathrm{d}\theta /\mathrm{d}z=U+\cdots dθ/dz=U+⋯
满足条件 θ ( ∞ ) = 1 \theta (\infty )=1 θ(∞)=1 的解是 θ = 1 \theta=1 θ=1。当 z → 0 + z\rightarrow 0^{+} z→0+,外部解的行为就像 θ = 1 \theta =1 θ=1,因此 d θ / d z = 0 \mathrm{d}\theta /\mathrm{d}z=0 dθ/dz=0。
我们可以看到,虽然在 z = 0 z=0 z=0 处, θ \theta θ 是连续的, d θ / d z \mathrm{d}\theta /\mathrm{d}z dθ/dz 在 z = 0 z=0 z=0 处有一个跳跃。导数之间的过渡由内部区域描述。
内部区域
在内部区域 1 − θ ∼ 1 / β 1-\theta \sim 1/\beta 1−θ∼1/β,反应项不再可以忽略不计。为了研究内层结构,引入了一个包含点 z = 0 z=0 z=0 的拉伸坐标,因为那是 θ \theta θ 根据外解趋近于一(unity),而拉伸因变量则根据 η = β z \eta =\beta z η=βz, Θ = β ( 1 − θ ) \Theta =\beta (1-\theta ) Θ=β(1−θ)。将这些变量代入控制方程并仅收集主导项(leading order terms),我们得到:
2 d 2 Θ d η 2 = Θ e − Θ 2{\frac {\mathrm{d}^{2}\Theta }{\mathrm{d}\eta ^{2}}}=\Theta e^{-\Theta } 2dη2d2Θ=Θe−Θ
当 η → − ∞ \eta\rightarrow -\infty η→−∞,边界条件为来自先前获得的外部解的局部行为,当我们用内部区域坐标来写时,它变成 Θ → − U η = + ∞ \Theta \rightarrow -U\eta =+\infty Θ→−Uη=+∞ 和 d Θ / d η = − U \mathrm{d}\Theta /\mathrm{d}\eta =-U dΘ/dη=−U。同样,当 η → ∞ \eta \rightarrow \infty η→∞,我们发现 Θ = d Θ / d η = 0 \Theta =\mathrm{d}\Theta /\mathrm{d}\eta =0 Θ=dΘ/dη=0。施加这些边界条件后,上述方程的第一个积分变为:
( d Θ d η ) 2 ∣ Θ = ∞ − ( d Θ d η ) 2 ∣ Θ = 0 = ∫ 0 ∞ Θ e − Θ d Θ U 2 = 1 {\displaystyle {\begin{aligned}\left.\left({\frac {\mathrm{d}\Theta }{\mathrm{d}\eta }}\right)^{2}\right|_{\Theta =\infty }-\left.\left({\frac {\mathrm{d}\Theta }{\mathrm{d}\eta }}\right)^{2}\right|_{\Theta =0}&=\int _{0}^{\infty }\Theta e^{-\Theta }\mathrm{d}\Theta \\U^{2}&=1\end{aligned}}} (dηdΘ)2 Θ=∞−(dηdΘ)2 Θ=0U2=∫0∞Θe−ΘdΘ=1
这意味着 U = 1 U=1 U=1。从第一个积分很清楚,波速平方 U 2 U^{2} U2 与积分(相对于 θ \theta θ)值 ω \omega ω 成正比(当然,在大 β \beta β 极限下,只有内部区域对这个积分有贡献)。代入 U = 1 U=1 U=1 后的第一个积分:
d Θ d η = − 1 − ( Θ + 1 ) exp ( − Θ ) . {\displaystyle {\frac {\mathrm{d}\Theta }{\mathrm{d}\eta }}=-{\sqrt {1-(\Theta +1)\exp(-\Theta )}}.} dηdΘ=−1−(Θ+1)exp(−Θ).
KPP-ZFK 转变
在 KPP 机制下, U m i n = U K P P U_{min}=U_{KPP} Umin=UKPP。对于这里使用的反应项,适用于 β ≪ 1 \beta \ll 1 β≪1的 KPP 速度由下式给出:
U K P P = 2 d ω d θ ∣ θ = 0 = 2 β e − β / 2 {\displaystyle U_{KPP}=2{\sqrt {\left.{\frac {\mathrm{d}\omega }{\mathrm{d}\theta }}\right|_{\theta =0}}}={\sqrt {2}} \beta e^{-\beta /2}} UKPP=2dθdω θ=0=2βe−β/2
而在 ZFK 机制中,正如我们在上面看到的 U Z F K = 1 U_{ZFK}=1 UZFK=1。方程对于各种 β \beta β 值的数值积分表明存在临界值 β ∗ = 1.64 \beta _{*}=1.64 β∗=1.64。这样只有 β ≤ β ∗ \beta \leq \beta _{*} β≤β∗, U m i n = U K P P U_{min}=U_{KPP} Umin=UKPP。对于 β ≥ β ∗ \beta \geq \beta _{*} β≥β∗, U m i n U_{min} Umin 大于 U K P P U_{KPP} UKPP。当 β ≫ 1 \beta \gg 1 β≫1, U m i n U_{min} Umin 趋近于 U Z F K = 1 U_{ZFK}=1 UZFK=1,从而接近 ZFK 机制。KPP 机制和 ZFK 机制之间的区域称为 KPP-ZFK 过渡区(transition zone)。
临界值取决于反应模型,例如我们得到:
β ∗ = 3.04 for ω ∝ ( 1 − θ ) e − β ( 1 − θ ) β ∗ = 5.11 for ω ∝ ( 1 − θ ) 2 e − β ( 1 − θ ) {\displaystyle \beta _{*}=3.04\quad {\text{for}}\quad \omega \propto (1-\theta )e^{-\beta (1-\theta )}}\\ {\displaystyle \beta _{*}=5.11\quad {\text{for}}\quad \omega \propto (1-\theta )^{2}e^{-\beta (1-\theta )}} β∗=3.04forω∝(1−θ)e−β(1−θ)β∗=5.11forω∝(1−θ)2e−β(1−θ)
Clavin–Liñán 模型
为了分析地预测 KPP-ZFK 转变,Paul Clavin 和 Amable Liñán 提出了一个简单的分段线性模型:
ω ( θ ) = { θ if 0 ≤ θ ≤ 1 − ϵ , h ( 1 − θ ) / ϵ 2 if 1 − ϵ ≤ θ ≤ 1 {\displaystyle \omega (\theta )={\begin{cases}\theta \quad {\text{if}}\quad 0\leq \theta \leq 1-\epsilon ,\\h(1-\theta ) /\epsilon ^{2}\quad {\text{if}}\quad 1-\epsilon \leq \theta \leq 1\end{cases}}} ω(θ)={θif0≤θ≤1−ϵ,h(1−θ)/ϵ2if1−ϵ≤θ≤1
其中 h ℎ h 和 ϵ \epsilon ϵ 是常数。模型的 KPP 速度为 U K P P = 2 U_{KPP}=2 UKPP=2,而在双极限 ϵ → 0 \epsilon \rightarrow 0 ϵ→0 和 h → ∞ ℎ\rightarrow \infty h→∞,ZFK 速度为 U Z F K = h U_{ZFK}={\sqrt {h}} UZFK=h,模拟 θ = 1 \theta=1 θ=1 附近反应的急剧增加。
对于这个模型,存在一个临界值 h ∗ = 1 − ϵ 2 h_{*}=1-\epsilon ^{2} h∗=1−ϵ2,这样:
{ h < h ∗ : U m i n = U K P P , h > h ∗ : U m i n = h / ( 1 − ϵ ) + 1 − ϵ h / ( 1 − ϵ ) − ϵ , h ≫ h ∗ : U m i n → U Z F K {\displaystyle {\begin{cases}h<h_{*}:&\quad U_{\mathrm{min}}=U_{KPP},\\h>h_{*}:&\quad U_{\mathrm{min}}={\frac { h/(1-\epsilon )+1-\epsilon }{\sqrt {h/(1-\epsilon )-\epsilon }}},\\h\gg h_{*}:&\quad U_{\mathrm{min}} \rightarrow U_{ZFK}\end{cases}}} ⎩ ⎨ ⎧h<h∗:h>h∗:h≫h∗:Umin=UKPP,Umin=h/(1−ϵ)−ϵh/(1−ϵ)+1−ϵ,Umin→UZFK
应用和普遍性
最近,反应-扩散系统作为图案形成的原型模型引起了人们的极大兴趣。上述模式(前沿(fronts)、螺旋、目标、六边形、条纹和耗散孤子)可以在各种类型的反应扩散系统中找到,尽管差异很大,例如在局域反应方面。还有人认为,反应-扩散过程是生物学中与形态发生相关过程的重要基础,甚至可能与动物皮毛和皮肤色素沉着有关。反应扩散方程的其他应用包括生态入侵、流行病传播、肿瘤生长、裂变波动力学和伤口愈合。对反应扩散系统感兴趣的另一个原因是,尽管它们是非线性偏微分方程,但通常有可能进行分析处理。
指纹的生成
独一无二的存在
人们常说,世上没有两片完全相同的树叶。其实,人的指纹也同样如此。一直以来,指纹的这种独一无二的特性,使它们长期被用于个人身份的识别。
过去,科学家们已经提出几种不同的理论来解释指纹的形成,比如之前有研究认为,基因在指纹的生长过程中,起到了重要作用。然而这无法解释为什么连同卵双胞胎也拥有不同的指纹。
现在,在一项新发表于《细胞》杂志的研究中,一个研究团队终于揭开了指纹形成的生化机制。他们发现,每个人指尖的独特指纹,是由三种信号分子,以及手指形状和皮肤生长时间的细微差异,共同创造的。
三种重要的信号分子
我们指尖之上的凹凸纹路,形成于胎儿发育的早期。人们认为,这些微小的脊状凸起结构可以增加指尖的抓力和敏感度,并且它们的图样可以帮助我们对一些发育状况进行诊断。
根据纹路的图样,指纹主要可以分为三种类型:呈三角形的弓形纹,长长且、的弯曲的箕形纹,以及对称的呈圆形的斗形纹。

为了确定在指纹的形成过程中所表达的基因,研究人员对人类胚胎指尖的细胞核内的RNA进行了测序,发现了三种在指导指尖皮肤的生长中发挥了重要作用的信号分子(在细胞之间传递信息的信使):WNT、BMP和EDAR。这三种信号分子共同控制了主要的脊状凸起的形成,衍化出了指纹的波纹结构。
小鼠“指纹”带来的启示
为了进一步研究这些信号分子是如何相互作用并形成纹路的,研究人员对小鼠的“指纹”进行了分析。小鼠的脚趾皮肤上也有简单的脊状凸起,可以将其与人类的指纹相比较。
通过控制小鼠体内的分子水平,他们发现,涉及到WNT和BMP这两种信号分子的基因,会在发育中的指尖细胞中以交替的条纹形式进行表达。当研究人员敲除WNT信号分子通路时,小鼠的脚趾上完全没有形成脊状凸起;而当BMP被敲除时,脊状凸起变得更宽了。
用简单的话来说,这意味着BMP会抑制细胞生长,在皮肤外层形成凹槽;WNT可以让细胞增殖,在皮肤上形成脊状凸起。
与此同时,他们发现EDAR与脊状凸起的粗细和间距有关:增加EDAR会导致小鼠的脚趾上出现更粗的、间距更宽的脊状凸起;而减少EDAR则会导致小鼠的脚趾上出现斑点状的凸起,而非条纹状的凸起。
时间、位置、形状,都很关键
WNT和BMP的这种对立关系,是图灵反应-扩散控制系统的一种标志性特征。这种系统由阿兰·图灵在20世纪50年代提出,它描述了化学物质如何相互作用和扩散,解释了自然界中出现的那些可见模式,比如植物叶片的排列,热带鱼身上的斑点或条纹等。
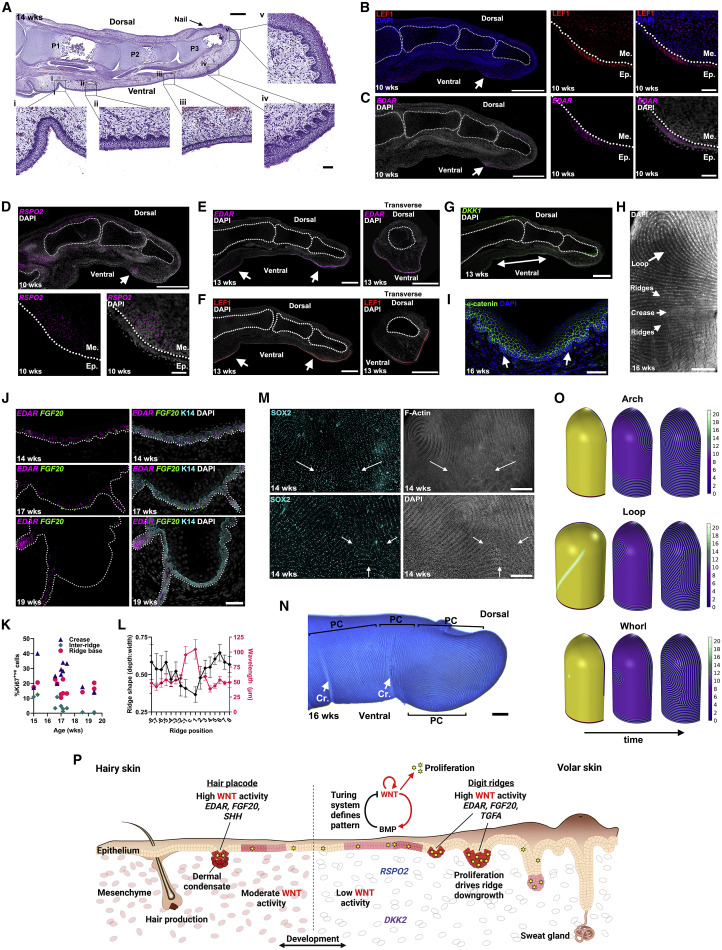
由于小鼠的脚趾太小,无法形成人类指纹那样的精致形状,因此在这项研究中,研究团队需要依靠计算机模型来模拟指纹的图灵斑图的扩散。已知在人类胚胎组织中,主要的脊状凸起始于指尖上的三个位置:柔软隆起的指垫的中心,指甲下的手指末端,以及最靠近指尖的关节折痕处。
于是,研究人员模拟了从这三个起始位置开始扩散的图灵斑图。通过让这些扩散起始于相对不同的时间、位置和角度,研究人员创造出了三种最常见的指纹模式——弓形纹、箕形纹和斗形纹,甚至还得出了一些更罕见的指纹模式。这表明,指纹图样的最终整体形状,还取决于手指的形状,以及脊状凸起形成的确切时间。
这是一项非常出色的研究,是理解指纹图样的一个重大进步。过去那些对皮肤纹路的研究往往更多地关注理论和建模方法,而非实验数据。但新的研究利用细胞培养技术和其他方法来推动了这一领域的实验方法的发展,大大地拓展了这一领域。让科学家有更多的机会关注隐藏在皮肤中的这些模式,了解皮肤的形成和发展。
实验
到目前为止,化学反应-扩散系统中的可控实验已经通过三种方式实现。首先,可以使用凝胶反应器或填充毛细管。其次,研究了催化表面(catalytic surface)的温度脉冲。第三,使用反应-扩散系统对运行神经脉冲的传播进行建模。
除了这些一般的例子,事实证明,在适当的情况下,电传输系统如等离子体或半导体可以用反应-扩散方法来描述。对于这些系统,已经进行了关于图案形成的各种实验。
数值处理
反应-扩散系统可以用数值数学方法求解。研究文献中已有几种数值处理。还针对复杂的几何形状提出了数值求解方法。为了最详细地描述反应扩散系统,使用基于粒子的模拟工具(如 SRSim 或 ReaDDy)进行描述,这些工具采用例如可逆相互作用粒子反应动力学(reversible interacting-particle reaction dynamics)。
演示工具
-
Reaction–Diffusion by the Gray–Scott Model: Pearson’s parameterization a visual map of the parameter space of Gray–Scott reaction diffusion.
-
Interactive web application for reaction-diffusion simulation
- 参考文献
wiki: Reaction–diffusion system
wiki: Fisher’s equation
Noise-induced order
wiki: Belousov–Zhabotinsky reaction
Glover, J. D. et al. Cell. The developmental basis of fingerprint pattern formation and variation. https://doi.org/10.1016/j.cell.2023.01.015 (2023).
How fingerprints form was a mystery — until now
How fingerprints get their one-of-a-kind swirls
Why don’t identical twins have the same fingerprints? New study provides clues
为什么指纹独一无二?现在终于有答案了
wki: ZFK equation