目录

题目描述

解题思路

 代码部分

---

题目描述

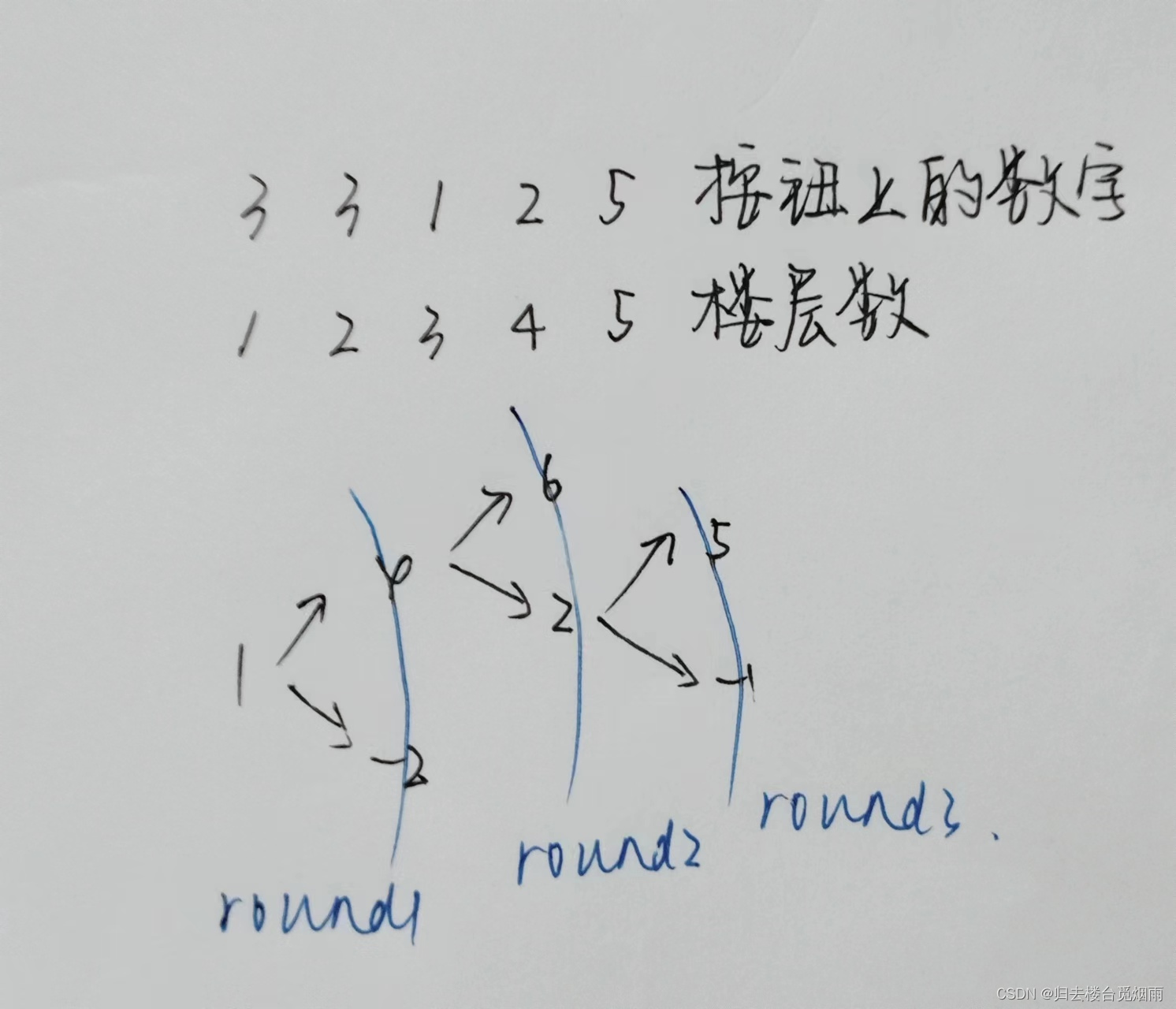
大楼的每一层楼都可以停电梯，而且第i层楼（1≤i≤N）上有一个数字Ki(0≤=Ki≤=N）。电梯只有四个按钮：开，关，上，下。上下的层数等于当前楼层上的那个数字。当然，如果不能满足要求，相应的按钮就会失灵。例如：3 3 1 2 5代表了（K1=3,K2=3,……），从一楼开始。在一楼，按“上”可以到4楼，按“下”是不起作用的，因为没有-2楼。那么，从A楼到B楼至少要按几次按钮呢？

输入

共有二行，第一行为三个用空格隔开的正整数，表示N,A,B(1≤N≤200, 1≤A,B≤N)，第二行为N个用空格隔开的正整数，表示Ki。

输出

一行，即最少按键次数,若无法到达，则输出-1。

样例输入

5 1 5
3 3 1 2 5

样例输出

3

解题思路

对于任意一层楼的楼梯，在该层都有一个数字按钮。这层楼至多可以通往两层楼。

应用队列思想。建立队列，传入初始值。

从队首取元素，判断这个元素代表的楼层可能到达的两个楼层“是否合法”。

如果合法，从队尾追加到队列之中，同时执行步数标记，又走了一步；如果不合法，舍弃。

判断循环终止条件：这道题如果能够成功到达目标楼层，即某次循环初队首元素刚好与目标层数字相等，可以提前终止循环；如果所有搜索结束后，队首元素一直不是目标楼层的层数，那么说明无法成功到达目标楼层，输出-1。

为什么这样做一定是最短路径：

关键词：广度搜索、优先输出。

将最短路径的问题转化为最先输出队列的问题。

本题与题目《1947抓住那头牛》方法类似。详情请参见

https://blog.csdn.net/bc202205/article/details/128986357

 代码部分

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 201;
int len[N];//路径标记
int a[N];//每层电梯上的特定数字的储存
int main()
{
	int n, former, latter;
	cin >> n >> former >> latter;
	for (int i = 1; i <= n; i++)
		cin >> a[i];
	int flag = 0;//标记是否能够成功运行
	memset(len, -1, sizeof(len));//路径初始化
	len[former] = 0;//路径赋初值
	queue<int>q;
	q.push(former);//将第一个元素推入队中
	int head; int temp1, temp2;//为了书写方便，
    //将某次取的队首元素提取出来，同时求出队首元素可能移动到的位置
	while (!q.empty())
	{
		head = q.front();
		if (head == latter)
		{
			flag = 1;//成功到达，标记为true
			break;
		}
		q.pop();//弹出队首元素
		temp1 = head + a[head];//可能到达的位置1
		temp2 = head - a[head];//可能到达的位置2
		if (temp1 > 0 && temp1 <= n && len[temp1]==-1)
        //如果楼层合法&&不往回走&&不走别人的路
		{
			len[temp1] = len[head] + 1;//从一步走到下一步，下一步标记
			q.push(temp1);//推入合法的temp1
		}
		if (temp2 > 0 && temp2 <= n && len[temp2]==-1)//同理
		{
			len[temp2] = len[head] + 1;
			q.push(temp2);
		}
	}
	if (flag)cout << len[latter];//如果标记为1，证明电梯成功到达latter楼，输出路径标记
	else cout << "-1";//如果标记为0，证明电梯无法到达latter楼，输出-1
	return 0;
}