2016-ICLR-Order Matters- Sequence to sequence for sets

Paper: [https://arxiv.org/pdf/1511.06391.pdf](https://arxiv.org/pdf/1511.06391.pdf)
Code:

顺序重要性：集合的顺序到序列

摘要

许多需要从观察序列映射或映射到观察序列的复杂任务现在可以使用序列到序列（seq2seq）框架来制定，该框架使用链规则来有效地表示序列的联合概率。然而，在许多情况下，可变大小的输入和/或输出可能不会自然地表示为序列。因此，作者讨论 seq2seq 框架的扩展，该框架超越序列并以原则的方式处理输入集。此外，作者提出了一个损失，通过在训练期间搜索可能的顺序，处理输出集结构的缺乏。并展示了关于排序的主张的经验证据，以及对基准语言建模和解析任务的seq2seq框架的修改，以及两个人工任务 - 排序数字和估计未知图形模型的联合概率。

序列和集合的神经网络

考虑一个具有 $n$ 对 $(X_i, Y_i)^n_{i=1}$ 的给定训练集的通用监督任务，其中 $X_i, Y_i)$ 是输入的第 $i$ i 对及其相应的目标。序列到序列范式对应于 $X_i$ 和 $Y_i$ 都由长度可能不同的序列表示的任务： $X_i = \{x^i_1, x^i_2,...,x^i_{si}\}$ 和 $Y_i = \{y^i_1, y^i_2, …, y^i_{ti} \}$ 。在这种情况下，使用条件概率 $P (Y ∣ X)$ 对每个示例建模并使用链式法则将其分解如下

并将其实现为编码器递归神经网络（RNN, 以按顺序读取每个 $x_s \in X$ ，如下所示：

其中 $h_s$ 是编码器在时间 s 的状态，后跟解码器 RNN 以在给定当前状态 $g_t$ 和之前的 $y_{t−1}$ 符号的情况下，一次生成一个 $y_t \in Y$ ：

输入集

原则上，当使用复杂编码器（如递归神经网络）时，顺序无关紧要，因为这些是通用近似器，可以从输入序列（例如，任何顺序的 n 元语法）对复杂特征进行编码。作者认为，顺序似乎很重要的原因是由于潜在的非凸优化和更合适的先验。并且输入数据向模型显示的顺序会影响学习性能。

注意力机制（重要，主要公式）

在此，作者采用了基于“content”的注意力。它具有以下特性：如果随机排序内存，从内存中检索到的向量不会改变。这对于正确处理输入集 $X$ 本身至关重要。基于注意力机制的流程块使用以下功能：

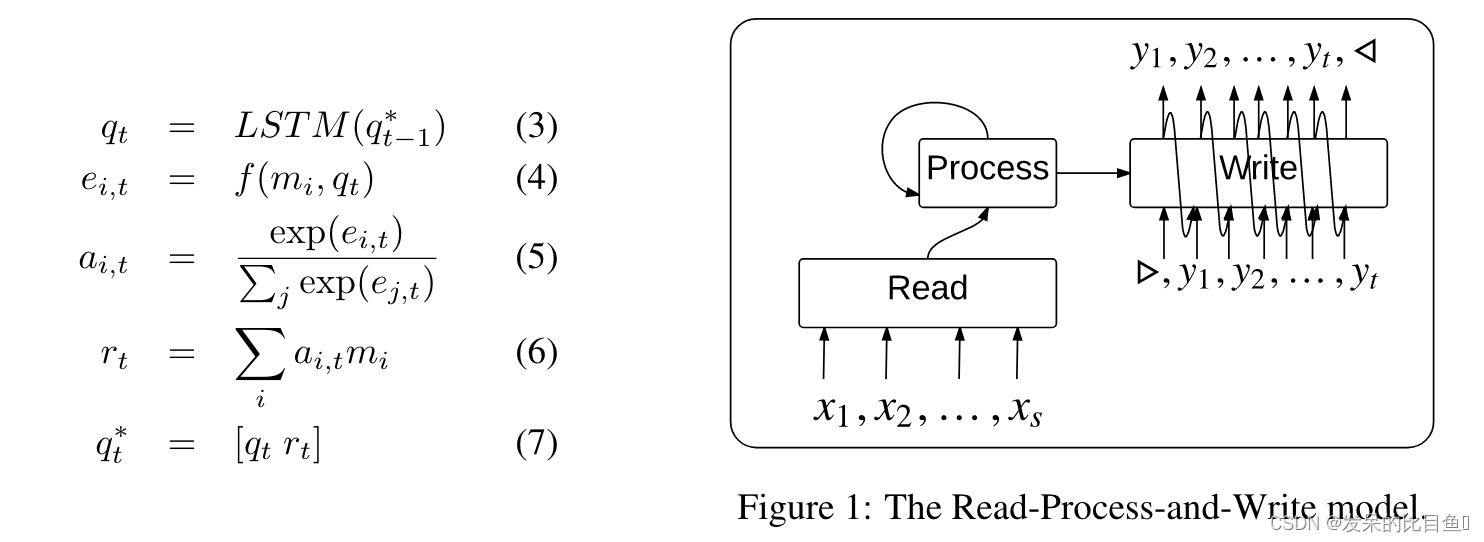
其中 $i$ 通过每个内存向量 $m_i$ （通常等于 X 的基数）进行索引， $q_t$ 是一个查询向量，允许从内存中读取 $r_t$ ， $f$ 是一个从 $m_i$ 和 $q_t$ 计算单个标量的函数（例如，点积），LSTM 是一个计算循环状态但不带输入的模型。 $q^∗ _t$ 是此 LSTM 演变的状态，通过将查询 $q_t$ 与生成的注意力读出 $r_t$ 连接起来而形成。 $t$ 是指示要提供给解码器的状态所携带多少“处理步骤”的索引。请注意，排列 $m_i$ 和 $m_{i′}$ 对读取向量 $r_t$ 没有影响。

读取、处理、写入

有三个组成部分:

一个读取块，它使用一个小神经网络简单地将每个元素 $x_i \in X$ 嵌入到一个记忆向量 $m_i$ （所有 $i$ 使用相同的神经网络）。
一个进程块，它是一个没有输入或输出的LSTM，在存储器 $m_i$ 上执行 $T$ T级计算。
一个写块，它是一个 LSTM 指针网络，它接收 $q^∗_T$ （作为从输入集产生输出所需的上下文），并指向 $m_i$ 的元素（隐式地, $x_i$ ), 一次一个步骤。

输出顺序的重要性

已经考虑了编码输入集的问题; 把注意力转向输出表示。描述随机变量 Y 集合上的联合概率的链式规则可能是联合概率的最简单分解，它不会产生任意限制（例如条件独立性）。

结论

LSTM已被证明是表示可变长度顺序数据的强大模型，这要归功于它们能够处理合理的长期依赖关系，并且使用链式规则有效地分解联合分布。另一方面，有些问题表现为一组无序的元素，要么作为输入，要么作为输出;在其他一些情况下，数据由一些需要线性化才能馈送到 LSTM 的结构表示，并且可能有多种方法可以做到这一点。

代码

来自于torchdrug

class Set2Set(Readout):
    def __init__(self, input_dim, type="node", num_step=3, num_lstm_layer=1):
        super(Set2Set, self).__init__(type)
        self.input_dim = input_dim
        self.output_dim = self.input_dim * 2
        self.num_step = num_step
        self.lstm = nn.LSTM(input_dim * 2, input_dim, num_lstm_layer)
        self.softmax = Softmax(type)

    def forward(self, graph, input):
 ensor: graph representations
        """
        input2graph = self.get_index2graph(graph)
        hx = (torch.zeros(self.lstm.num_layers, graph.batch_size, self.lstm.hidden_size, device=input.device),) * 2 # [bi*num_lyers, batch, hz]
        query_star = torch.zeros(graph.batch_size, self.output_dim, device=input.device) #[seq_len, batch, input_dim]

        for i in range(self.num_step):
            query, hx = self.lstm(query_star.unsqueeze(0), hx) #[seq_len, bz, bi*hz], [bi*nlayers, batch, hz]
            query = query.squeeze(0)
            product = torch.einsum("bd, bd -> b", query[input2graph], input) #
            attention = self.softmax(graph, product) # batch内节点对每个batch的注意力
            output = scatter_add(attention.unsqueeze(-1) * input, input2graph, dim=0, dim_size=graph.batch_size)
            query_star = torch.cat([query, output], dim=-1)

        return query_star