目录

1 问题背景

1.1计算图（Computational Graph）

1.2 激活函数（Activation Function）引入

1.3 问题引入

2 反向传播（Back Propagation）

2.1 为什么要使用反向传播

2.2 前馈运算(Forward Propagation)过程

2.3 反向传播过程

2.3.1 计算过程 

2.3.2 课堂练习

3 在Pytorch中进行前馈和反向传播计算

3.1 Tensor数据类型

3.2 代码实现

3.2.1 实现线性模型

---

1 问题背景

1.1计算图（Computational Graph）

计算图（Computational Graph）是一种用于表示数学运算的图形模型。在计算图中，每个节点代表一个数学运算，而每条边代表运算之间的输入输出关系。

计算图用于记录和组织复杂的数学运算，可以帮助我们快速理解运算的依赖关系和结构。在机器学习和深度学习中，计算图是一种常用的工具，用于定义和计算模型的损失函数和梯度。

计算图还可以用于求导，通过利用计算图上的梯度进行反向传播，可以快速计算模型的损失函数对于每个参数的导数。因此，计算图不仅提高了计算效率，而且可以方便地实现自动微分和反向传播。

比如下式

 用计算图表示

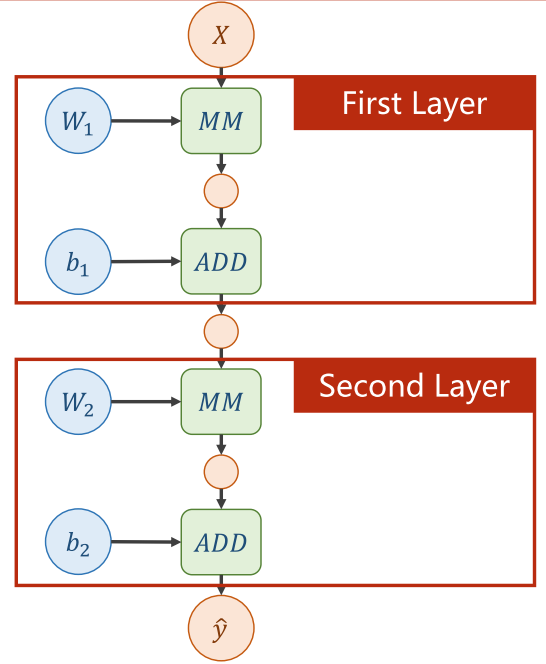
 注：MM表示相乘

1.2 激活函数（Activation Function）引入

对于刚刚举例的神经网络计算图，计算机会直接对其进行简化：

 

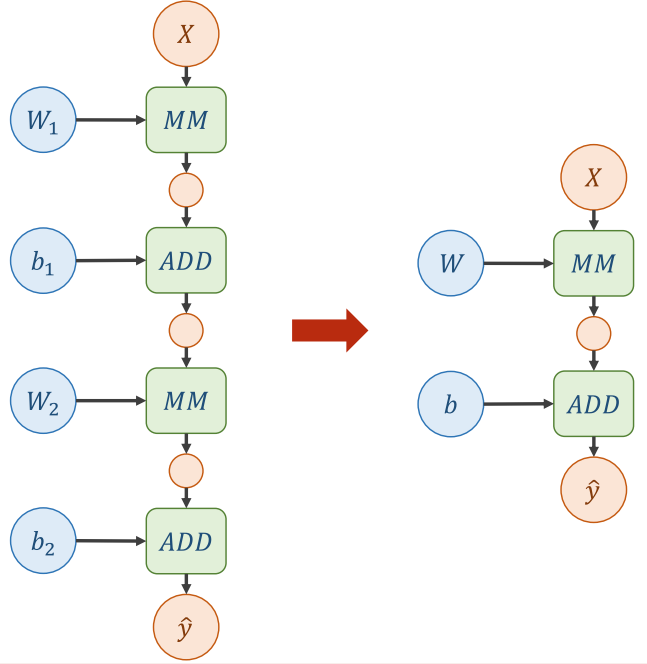
 这就导致了计算过程中添加的新的权重值变得毫无意义，层数的划分变得多余，导致神经网络的表示能力下降。

  为了解决这个问题，我们需要在每一层的输出处应用上一个非线性变换函数(Nonlinear
Function)，这样模型就不会被简化了

  如果一个神经网络只使用线性变换函数，那么其最终的表示能力仍然有限，因为它们的输出结果是线性的，无法对复杂的数据进行分类或回归。因此，在每一层的输出都应用非线性变换函数，以增强神经网络的表示能力。

  非线性变换函数通常也称为激活函数（Activation Function）。常见的激活函数有Sigmoid函数、ReLU函数等。

补充

线性函数与非线性函数的简单区别：线性函数其函数图像是一条直线；非线性函数的函数图像是一条曲线，等等。

1.3 问题引入

对于一个简单线性模型 ，我们可以利用解析式来进行简单的计算。

 通过计算图，我们可以直观地看出计算的过程：

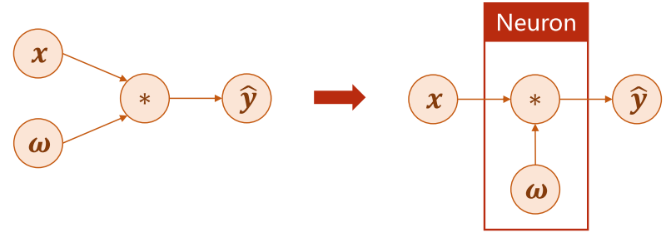
然后利用解析式来更新权重：

 但是对于复杂的神经网络模型来说，可能同时含有多个𝜔，如果为每个𝜔写解析式来计算，任务会非常繁重，且解析式也会变得很复杂：

  复杂的神经网络模型往往具有大量的权重，如果使用手动计算权重导数的方法，这将是一项非常复杂且繁琐的任务。

2 反向传播（Back Propagation）

2.1 为什么要使用反向传播

  如果使用手动计算权重导数的方法来计算复杂神经网络模型，将会非常困难。而反向传播（Back Propagation）可以使用链式法则自动计算损失函数对于每个权重的导数，大大减少计算复杂度，使训练神经网络变得更加有效。

  除此之外，反向传播还有一个优点：实现最优化，省去了重复求导的步骤，以及更高效地去计算偏导。详情请参考相关链接，这里不展开：

http://t.csdn.cn/igONJ
https://zhuanlan.zhihu.com/p/25081671

2.2 前馈运算(Forward Propagation)过程

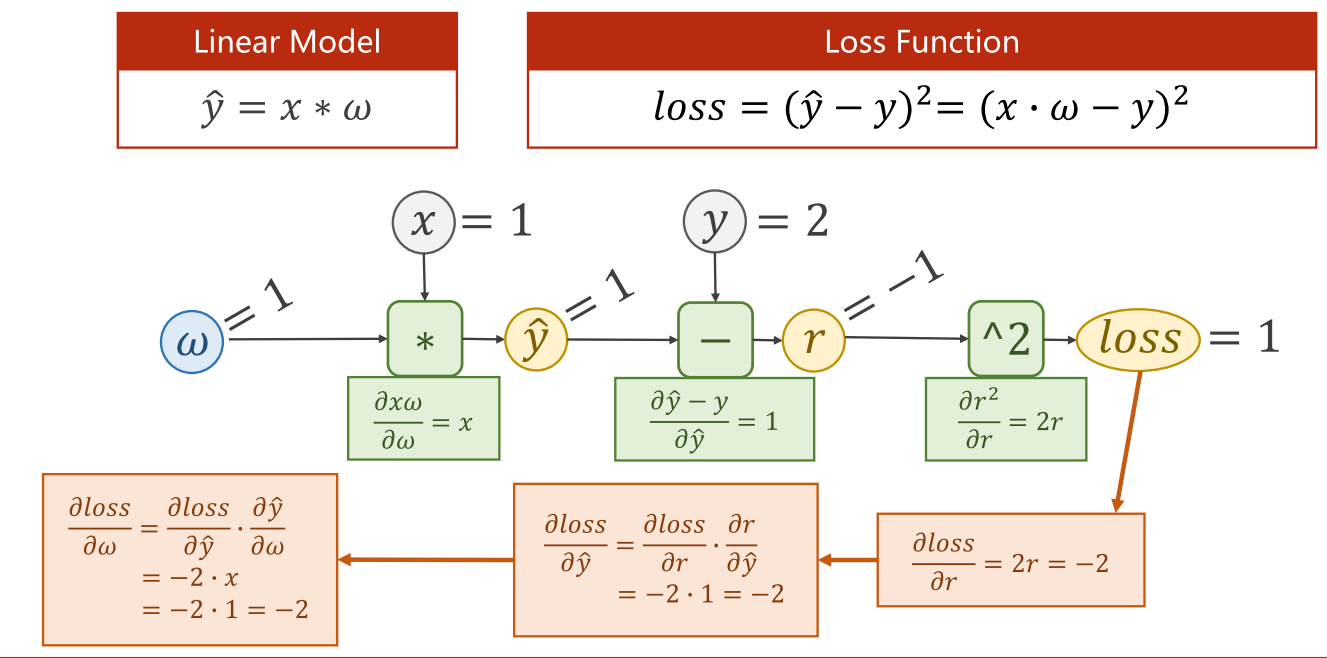
简单来说，就是 x和𝜔进行f(x, 𝜔)操作后得出z，然后把z值应用到Loss中去。

比如𝑓 = 𝑥 ∙ 𝜔, 𝑥 = 2, 𝜔 = 3

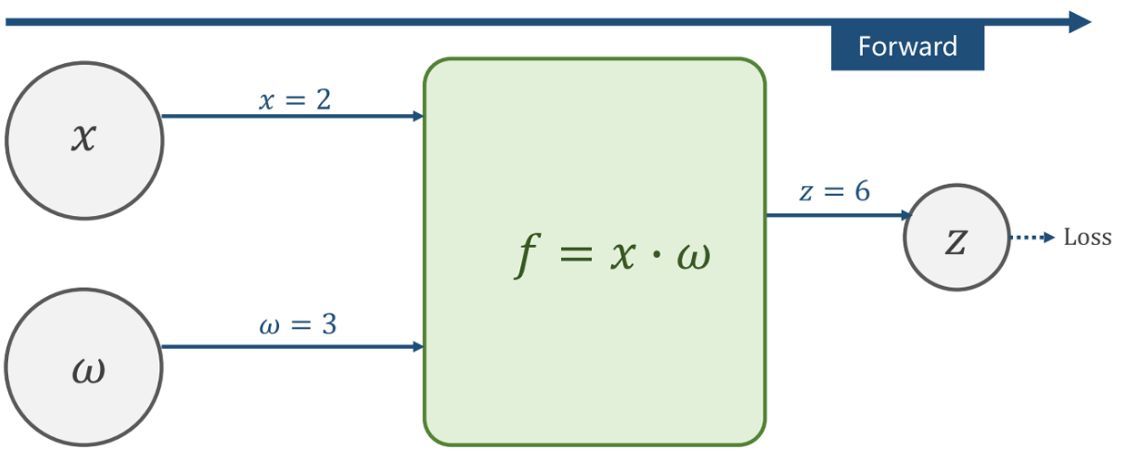
2.3 反向传播过程

2.3.1 计算过程 

 

其中以下两个局部函数是由z=𝑥 ∙ 𝜔，分别对x和对𝜔求导得到的：

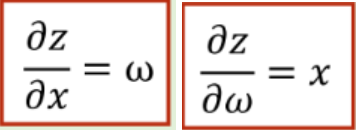
简单来说，就是沿着正方向相反的方向，为每个节点乘上局部导数后，再传递给下一个节点。

2.3.2 课堂练习

 (1)计算梯度

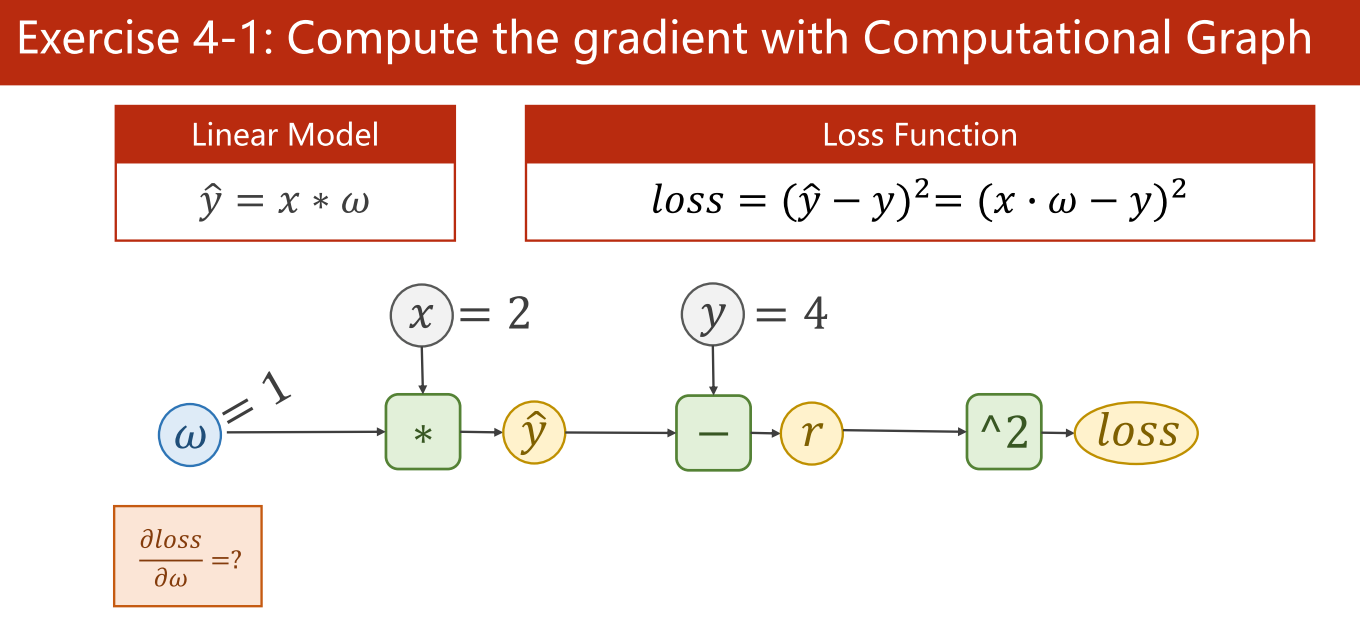
答案：-8

(2)计算加上偏差值后的梯度(计算仿射模型的梯度) 

 

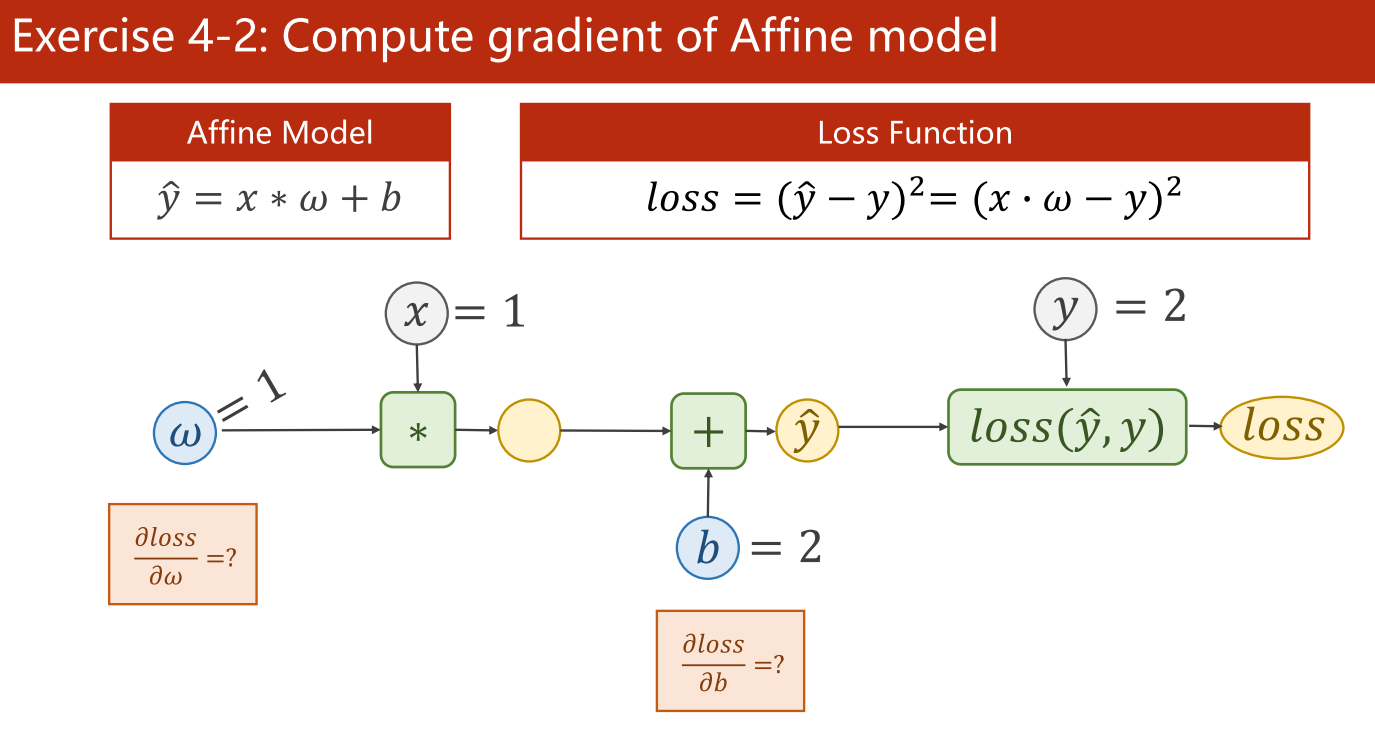
答案：2,2

3 在Pytorch中进行前馈和反向传播计算

3.1 Tensor数据类型

3.2 代码实现

3.2.1 实现线性模型

课堂上的案例，补充了些解释： 

import torch

x_data = [2.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = torch.Tensor([1.0])  # 创建了一个一维张量，包含单一数值1.0，作为权重初始值
w.requires_grad = True  #  w=torch.Tensor([1.0])创建了一个张量，然后使用 w.requires_grad = True设置该张量需要求导，于是PyTorch 会记录对该张量的操作，以便在反向传播时进行梯度更新


def forward(x):
    return x * w # 注意这里的x已经自动转换为Tensor类型,原本是list类型


def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2


print("predict (before training)", 4, forward(4).item())
for epoch in range(100):
    for x, y in zip(x_data, y_data):
        l = loss(x, y)

        # 反向传播，这句还可以清空释放计算图，避免计算图堆砌在内存中。
        # 若在当前backward()后，不执行forward() 而是执行另一个backward()，
        # 则需要在当前backward()时，指定保留计算图，backward(retain_graph)
        # 换言之，想要保留计算图，则写成backward(retain_graph)
        l.backward()

        # 使用item将一个张量转换成一个 Python标量，也是为了防止产生计算图
        # 一般在进行数学运算时使用grad.data，而在输出梯度数值时使用grad.item()
        # 一般梯度只有一个元素，所以使用.item()
        # 可以方便地把梯度值转换为一个数字。
        print('\tgrad:', x, y, w.grad.item())

        # 这句代码用来更新权重
        # 这里使用w.grad.data而不是w.grad是为了防止建立计算图，我们只是对数值做修改，而不是对模型做出修改
        # 虽然w.data 也是 tensor 类型的数据，
        # 但它是不需要 gradient 的，因此不会建立计算图，只是在数值范围上发生变化
        w.data = w.data - 0.01 * w.grad.data

        w.grad.data.zero_()  # 每次反向传播前，需要清空梯度缓存，以避免之前的梯度对当前梯度造成影响。

    print("progress:", epoch, l.item())  # 轮数，每轮训练完后对应的loss值，l是tensor类型，所以用item取出值来
print("predict (after training)", 4, forward(4).item())

简单来说，每一轮，数据都会先前馈运算出loss，再反向运算出新的梯度，然后用梯度来更新权重值。