凸优化问题
凸优化问题的广义定义:
- 目标函数为凸函数
- 约束集合为凸集
一、优化问题
基本用语
一般优化问题的描述:
minimize
f
0
(
x
)
subject to
f
i
(
x
)
⩽
0
,
i
=
1
,
⋯
,
m
h
i
(
x
)
=
0
,
i
=
1
,
⋯
,
p
(1)
\begin{array}{ll} \operatorname{minimize} & f_0(x) \\ \text { subject to } & f_i(x) \leqslant 0, \quad i=1, \cdots, m \\ & h_i(x)=0, \quad i=1, \cdots, p \end{array}\tag{1}
minimize subject to f0(x)fi(x)⩽0,i=1,⋯,mhi(x)=0,i=1,⋯,p(1)
相关定义:
x ∈ R n x\in \R^n x∈Rn:优化变量,optimization variable
f 0 : R n → R f_0:\R^n\rightarrow R f0:Rn→R:目标函数/损失函数,objective function/cost function
若是一个极大化问题,那么称为 效用函数 utility function
f i ( x ) ≤ 0 : R n → R f_i(x)\leq 0:\R^n\rightarrow \R fi(x)≤0:Rn→R:不等式约束,inequality constraint
h i ( x ) = 0 h_i(x)=0 hi(x)=0:等式约束 equality constraint
m = p = 0 m=p=0 m=p=0:无约束 unconstraited
优化问题的域:domain;所有函数定义域的交集
D
=
⋂
i
=
0
m
dom
f
i
∩
⋂
i
=
1
p
dom
h
i
\mathcal{D}=\bigcap_{i=0}^m \operatorname{dom} f_i \cap \bigcap_{i=1}^p \operatorname{dom} h_i
D=i=0⋂mdomfi∩i=1⋂pdomhi
可行解集:feasible set,使得问题约束满足的解的集合
注意,还需要在目标函数的定义域内
最优点与局部最优点
最优点与局部最优点:若可行解集合不是空集那么总是能在集合中找到一个X,使得目标函数最优,这个值称为最优值。
P
∗
=
inf
{
f
0
(
x
)
∣
X
∈
X
f
}
P^*=\inf \{f_0(x)|X\in X_f\}
P∗=inf{f0(x)∣X∈Xf}
若
X
f
X_f
Xf为空集,那么
P
∗
=
∞
P^*=\infty
P∗=∞
最优解:若 X ∗ X^* X∗可行,且 f 0 ( X ∗ ) = P ∗ f_0(X^*)=P^* f0(X∗)=P∗
最优解集:最优解的集合
X
o
p
t
=
{
X
∣
X
∈
X
f
,
f
0
(
X
)
=
P
∗
}
X_{opt}=\{X|X\in X_f,f_0(X)=P^*\}
Xopt={X∣X∈Xf,f0(X)=P∗}
ϵ
−
\epsilon-
ϵ−次优解集:satisficing solution

约束一般要满足,目标函数值不一定要达到最优值,可以离最优值小一定的距离
ϵ
\epsilon
ϵ
X
ϵ
=
{
X
∈
X
f
,
f
0
(
X
)
≤
P
∗
+
ϵ
}
X_{\epsilon}=\{X\in X_f,f_0(X)\leq P^*+\epsilon\}
Xϵ={X∈Xf,f0(X)≤P∗+ϵ}
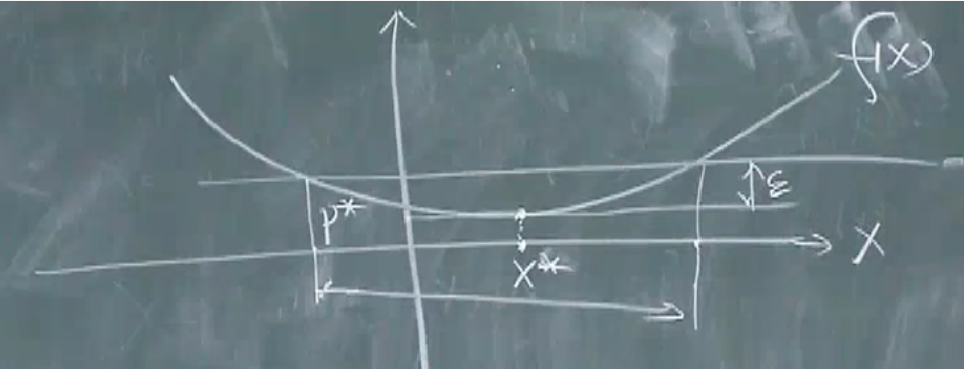
局部最优解:
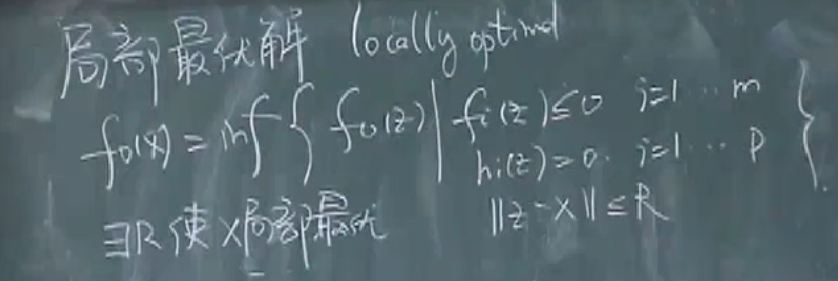
域、可行解集、全局最优解、局部最优解, ϵ \epsilon ϵ解集之间的关系:
若 x ∈ X f , f i ( x ) = 0 x\in X_f,f_i(x)=0 x∈Xf,fi(x)=0,则 f i ( x ) ≤ 0 f_i(x)\leq 0 fi(x)≤0为活动约束; f i ( x ) < 0 f_i(x)<0 fi(x)<0为不活动约束。
排除临界点的方法:

可行性优化问题
可行性优化问题一般可以写成下面的形式:
find
x
subject to
f
i
(
x
)
⩽
0
,
i
=
1
,
⋯
,
m
h
i
(
x
)
=
0
,
i
=
1
,
⋯
,
p
.
\begin{array}{ll} \text { find } & x \\ \text { subject to } & f_i(x) \leqslant 0, \quad i=1, \cdots, m \\ & h_i(x)=0, \quad i=1, \cdots, p . \end{array}
find subject to xfi(x)⩽0,i=1,⋯,mhi(x)=0,i=1,⋯,p.
如何写成标准的形式?写成最优化一个常数。
问题的标准表示
框约束 Box Constraints
minimize f 0 ( x ) subject to l 1 ≤ x i ≤ u i , i = 1 , . . . , n \begin{array}{ll} \text{minimize}& f_0(x)\\ \text{subject to}& l_1\leq x_i\leq u_i,i=1,...,n \end{array} minimizesubject tof0(x)l1≤xi≤ui,i=1,...,n
即每个变量都有一个上界和下界,那么可以转换为下面的标准形式:
minimize
f
0
(
x
)
subject to
l
i
−
x
i
≤
0
,
i
=
1
,
.
.
.
,
n
x
i
−
u
i
≤
0
,
i
=
1
,
.
.
.
,
n
\begin{array}{ll} \text{minimize}& f_0(x)\\ \text{subject to}& l_i-x_i\leq 0,i=1,...,n\\ & x_i-u_i\leq 0,i=1,...,n \end{array}
minimizesubject tof0(x)li−xi≤0,i=1,...,nxi−ui≤0,i=1,...,n
等价问题
如果从一个问题的解,很容易得到另一个问题的解,并且反之亦然,那么我们称两个问题是等价的。作为一个简单的例子,考虑:
minimize
f
~
(
x
)
=
α
0
f
0
(
x
)
subject to
f
~
i
(
x
)
=
α
i
f
i
(
x
)
⩽
0
,
i
=
1
,
⋯
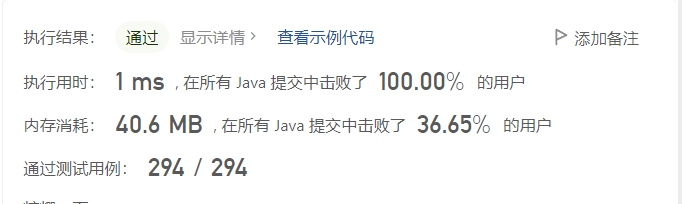
,
m
h
~
i
(
x
)
=
β
i
h
i
(
x
)
=
0
,
i
=
1
,
⋯
,
p
(2)
\begin{array}{ll} \operatorname{minimize} & \tilde{f}(x)=\alpha_0 f_0(x) \\ \text { subject to } & \tilde{f}_i(x)=\alpha_i f_i(x) \leqslant 0, \quad i=1, \cdots, m \\ & \tilde{h}_i(x)=\beta_i h_i(x)=0, \quad i=1, \cdots, p \end{array}\tag{2}
minimize subject to f~(x)=α0f0(x)f~i(x)=αifi(x)⩽0,i=1,⋯,mh~i(x)=βihi(x)=0,i=1,⋯,p(2)
很多时候约束的量级不同,量级过大导致约束的权重变化。通过等价转换,可以将问题的约束进行标准化。
目标函数和约束函数的变换
设:
ψ
0
:
R
→
R
\psi_0:\R\rightarrow \R
ψ0:R→R单增;
ψ
1
,
.
.
.
,
ψ
m
:
R
→
R
\psi_1,...,\psi_m:\R\rightarrow \R
ψ1,...,ψm:R→R满足:当且仅当
u
≤
0
u\leq 0
u≤0时
ψ
i
(
u
)
≤
0
;
ψ
m
+
1
,
.
.
.
,
ψ
m
+
p
:
R
→
R
\psi_i(u)\leq 0;\psi_{m+1},...,\psi_{m+p}:\R\rightarrow \R
ψi(u)≤0;ψm+1,...,ψm+p:R→R满足:当且仅当
u
=
0
u=0
u=0时
ψ
i
(
u
)
=
0
\psi_i(u)=0
ψi(u)=0。我们定义函数
f
~
i
\tilde f_i
f~i和
h
~
i
\tilde h_i
h~i为复合函数:
f
~
i
(
x
)
=
ψ
(
f
i
(
x
)
)
,
i
=
0
,
.
.
.
,
m
h
~
i
(
x
)
=
ψ
m
+
i
(
h
i
(
x
)
)
,
i
=
1
,
.
.
.
,
p
\tilde f_i(x)=\psi(f_i(x)),i=0,...,m\qquad \tilde{h}_i(x)=\psi_{m+i}(h_i(x)),i=1,...,p
f~i(x)=ψ(fi(x)),i=0,...,mh~i(x)=ψm+i(hi(x)),i=1,...,p
显然,问题
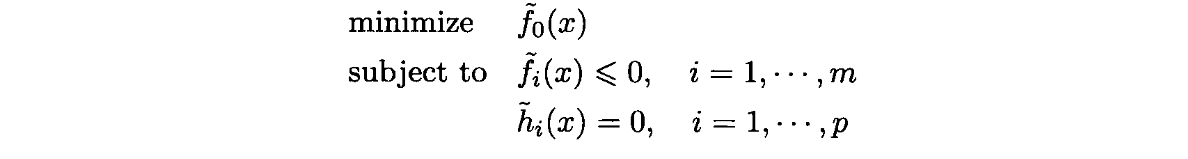
与标准形式式1等价且同解。并且式2是 ψ \psi ψ为线性函数的一种特例。
例:最小函数和最小范数平方问题
min
∣
∣
A
X
−
b
∣
∣
2
\min ||AX-b||_2
min∣∣AX−b∣∣2
上述问题是一个无约束的优化问题,等价于最小化二范数的平方。
min
∣
∣
A
X
−
b
∣
∣
2
2
\min ||AX-b||_2^2
min∣∣AX−b∣∣22
原因是原函数在实数域内单调递增。
松弛变量
f i ( x ) ≤ 0 f_i(x)\leq 0 fi(x)≤0等价于 ∃ s i ≥ 0 , f i ( x ) + s i ( x ) = 0 \exist s_i\geq 0,f_i(x)+s_i(x)=0 ∃si≥0,fi(x)+si(x)=0,将问题进行转换,得到:
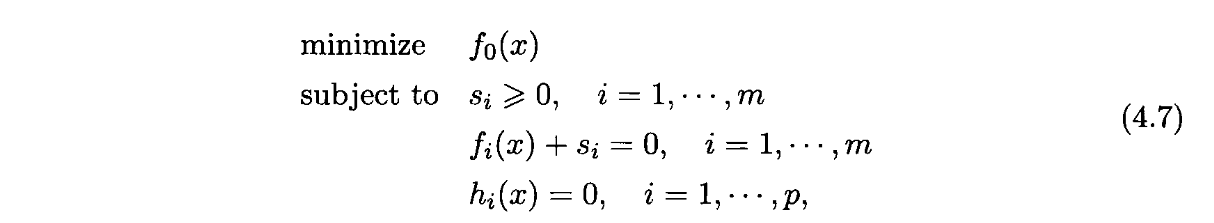
引入 s i s_i si后,问题就不仅是关于x的优化问题了。对于问题的凸性,需要对变量x和s同时验证。
进行松弛后,将变量的维数和约束都增加了。但有些时候,会通过松弛变量,将问题的结构转换为更加通用的结构。
等式约束的消除
例:等式约束的消除
对于优化问题而言,约束的数目越多,优化越复杂,所以消除等式约束是降低优化问题难度的一个重要方法。
{ h i ( x ) = 0 , i = 1 , . . . , p } (3) \{h_i(x)=0,i=1,...,p\}\tag{3} {hi(x)=0,i=1,...,p}(3)
是一组方程。假设我们能够得到这组方程的解,那么用一组参数
z
∈
R
k
z\in \R^k
z∈Rk来显式地参数化等式约束。设函数
ϕ
:
R
k
→
R
n
\phi:\R^k\rightarrow \R^n
ϕ:Rk→Rn是这样的函数:
x
x
x满足式(3)等价于存在一些
z
∈
R
k
z\in\R^k
z∈Rk,使得
x
=
ϕ
(
z
)
x=\phi(z)
x=ϕ(z)
那么优化问题
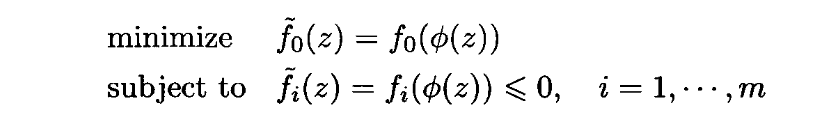
与原问题式1等价。求解出 z z z后,可由 x = ϕ ( z ) x=\phi(z) x=ϕ(z)得出最优解 x x x。
相当于用变量z去表示x,然后代入原目标函数和约束中。
等式定义了一组超平面,可以表示为特解+一组基的形式。
例:消除线性等式约束 A X − b = 0 AX-b=0 AX−b=0
A ∈ R p × n A\in \R^{p\times n} A∈Rp×n,是否能找到一组 z z z表示X呢?
分情况讨论:
- A X − b = 0 AX-b=0 AX−b=0无解,那么原问题无可行解
- 反之,令 x 0 x_0 x0为等式约束的任意可行解,那么通解可以表示为 F z + x 0 Fz+x_0 Fz+x0。即 ϕ ( z ) = F z + x 0 \phi (z)=Fz+x_0 ϕ(z)=Fz+x0
二、凸优化
标准形式的凸优化问题
凸优化问题是形如:
minimize
f
0
(
x
)
subject to
f
i
(
x
)
⩽
0
,
i
=
1
,
⋯
,
m
a
i
x
=
b
i
,
i
=
1
,
⋯
,
p
(4)
\begin{array}{ll} \operatorname{minimize} & f_0(x) \\ \text { subject to } & f_i(x) \leqslant 0, \quad i=1, \cdots, m \\ & a_i^x=b_i, \quad i=1, \cdots, p \end{array}\tag{4}
minimize subject to f0(x)fi(x)⩽0,i=1,⋯,maix=bi,i=1,⋯,p(4)
从广义上来说,如果目标函数是一个凸函数,约束的集合为凸集,那么问题就是凸问题。
狭义上的凸问题:
- 目标函数是凸函数
- 不等式约束的函数也是凸函数
- 等式约束函数是仿射函数
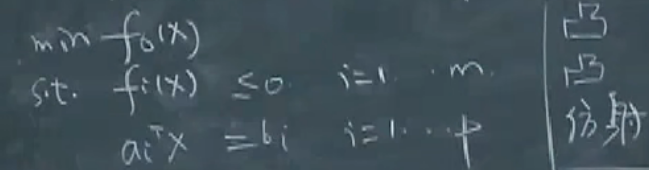
在这样的定义下,凸优化问题的可行域一定是凸的,因为他是问题定义域
D
=
⋂
i
=
0
m
d
o
m
f
i
\mathcal{D}=\bigcap_{i=0}^m\bold{dom}f_i
D=i=0⋂mdomfi
(凸集),m个下水平集,以及p个超平面的交集。因此,在凸优化问题中,我们是在一个凸集上极小化一个凸的函数。
若目标函数变为拟凸函数,那么该问题成为拟凸优化问题。但如果目标函数是凹函数,或者其他函数,那么我们统一称之为非凸优化问题。
例:
min
f
0
(
x
)
=
x
1
2
+
x
2
2
s.t.
{
f
1
(
x
)
:
x
1
1
+
x
2
2
≤
0
h
1
(
x
)
:
(
x
1
+
x
2
)
2
=
0
\min f_0(x)=x_1^2+x_2^2\\ \text{s.t.}\begin{cases}f_1(x):\frac{x_1}{1+x_2^2}\leq 0\\ h_1(x):(x_1+x_2)^2=0\end{cases}
minf0(x)=x12+x22s.t.{f1(x):1+x22x1≤0h1(x):(x1+x2)2=0
表面上看不是狭义的凸问题,可以转换为下面的形式:
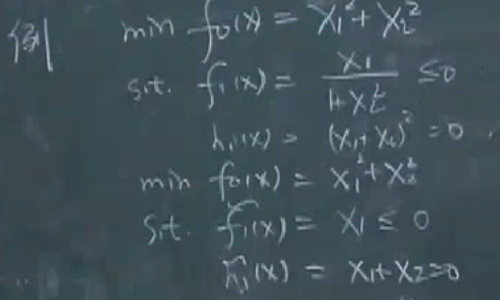
如果等式约束是一个放射约束,那么可利用等式约束对问题进行降维:
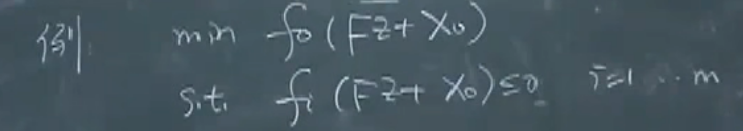
一般来说,不对问题进行降维,有必要的情况才会进行降维。
凹最大化问题
约束不变,若目标是最大化一个凹函数,那么等价于最小化一个凸函数,即,该情况下仍是凸优化问题。
max
f
0
(
x
)
⇔
min
−
f
0
(
x
)
\max f_0(x)\Leftrightarrow \min -f_0(x)
maxf0(x)⇔min−f0(x)
同理,如果
f
0
(
x
)
f_0(x)
f0(x)是拟凹的,那么最大化该问题被称为拟凹的。
局部最优解与全局最优解
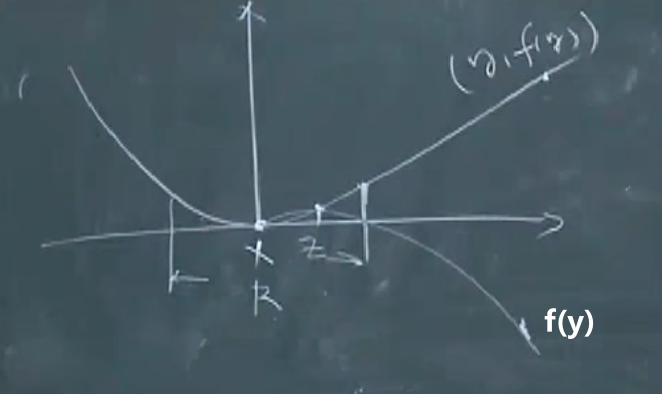
对于凸问题来说,局部最优解一定是全局最优解。
局部最优: ∃ R > 0 , f 0 ( x ) = inf { f 0 ( z ) ∣ z 可行 , x 可行 , ∣ ∣ x − z ∣ ∣ ≤ R } \exist R>0,f_0(x)=\inf \{f_0(z)|z可行,x可行,||x-z||\leq R\} ∃R>0,f0(x)=inf{f0(z)∣z可行,x可行,∣∣x−z∣∣≤R}
证明:
设 x x x不是全局最优解,即 ∃ y \exists y ∃y可行, f 0 ( y ) < f 0 ( x ) f_0(y)< f_0(x) f0(y)<f0(x)。
又因为 x x x是局部最优的,那么 ∣ ∣ y − x ∣ ∣ 2 > R ||y-x||_2> R ∣∣y−x∣∣2>R,那么可以构造出一个新的解: z = ( 1 − θ ) x + θ y , θ = R 2 ∣ ∣ y − x ∣ ∣ 2 ∈ [ 0 , 1 2 ] z=(1-\theta)x+\theta y,\theta=\frac{R}{2||y-x||_2}\in[0,\frac{1}{2}] z=(1−θ)x+θy,θ=2∣∣y−x∣∣2R∈[0,21],所以z是x和y的凸组合。又因为可行解集一定是个凸集,所以z一定在可行解集内,即 z z z可行。
又因为
f
0
(
x
)
f_0(x)
f0(x)是凸函数,故
f
0
(
z
)
≤
θ
f
0
(
x
)
+
(
1
−
θ
)
f
0
(
y
)
∣
∣
z
−
x
∣
∣
2
=
θ
∣
∣
x
−
y
∣
∣
2
=
R
2
(2.2)
f_0(z)\leq \theta f_0(x)+(1-\theta)f_0(y)\\ ||z-x||_2=\theta ||x-y||_2=\frac{R}{2}\tag{2.2}
f0(z)≤θf0(x)+(1−θ)f0(y)∣∣z−x∣∣2=θ∣∣x−y∣∣2=2R(2.2)
即
z
z
z在x的邻域内。因为x是局部最优解,故
f
0
(
x
)
<
f
0
(
z
)
f_0(x)<f_0(z)
f0(x)<f0(z)。
即,综上所述,需要满足下面的条件:
f
0
(
y
)
<
f
0
(
x
)
f
0
(
x
)
<
f
0
(
z
)
f_0(y)<f_0(x)\\ f_0(x)<f_0(z)
f0(y)<f0(x)f0(x)<f0(z)
即f
f
0
(
y
)
<
f
0
(
x
)
<
f
0
(
z
)
f_0(y)<f_0(x)<f_0(z)
f0(y)<f0(x)<f0(z)
与式2.2矛盾。故x一定是全局最优解。
图形表示:
可微函数 f 0 f_0 f0的最优性准则
可微凸问题目标函数的一阶条件:
f
0
(
y
)
≥
f
0
(
x
)
+
∇
f
0
T
(
x
)
⋅
(
y
−
x
)
∀
x
,
y
∈
d
o
m
f
f_0(y)\geq f_0(x)+\nabla f_0^T(x)\cdot (y-x)\qquad \forall x,y\in \bold{dom}f
f0(y)≥f0(x)+∇f0T(x)⋅(y−x)∀x,y∈domf
问题的可行域:
X
f
=
{
x
∣
f
i
(
x
)
≤
0
,
i
=
1
,
.
.
.
,
m
;
h
i
(
x
)
=
0
,
i
=
1
,
.
.
.
,
p
}
X_f=\{x|f_i(x)\leq 0,i=1,...,m;h_i(x)=0,i=1,...,p\}
Xf={x∣fi(x)≤0,i=1,...,m;hi(x)=0,i=1,...,p}
那么
X
∗
∈
X
f
X^*\in X_f
X∗∈Xf最优等价于
∇
f
0
T
(
X
∗
)
(
y
−
X
∗
)
≥
0
(2.3)
\nabla f_0^T(X^*)(y-X^*)\geq 0\tag{2.3}
∇f0T(X∗)(y−X∗)≥0(2.3)
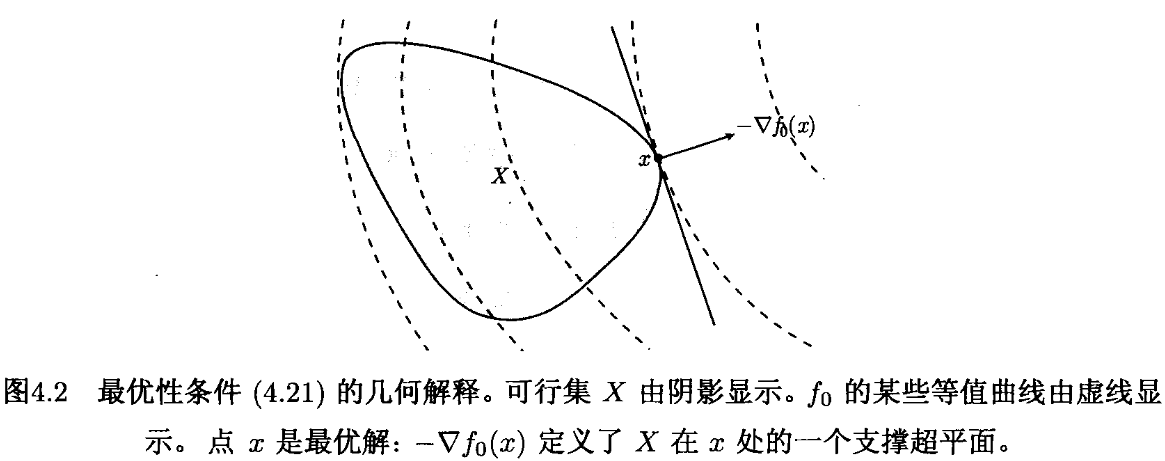
约束仅为等式约束
min f 0 ( x ) d o m f 0 = R n s . t . A X = b \min f_0(x)\\ \bold{dom}f_0=\R^n\\ s.t. AX=b minf0(x)domf0=Rns.t.AX=b
若 ∃ x , A X = b \exist x,AX=b ∃x,AX=b,那么X最优等价于 ∀ y , A y = b , ∇ f 0 T ( x ) ( y − x ) ≥ 0 \forall y,Ay=b,\nabla f_0^T(x)(y-x)\geq 0 ∀y,Ay=b,∇f0T(x)(y−x)≥0成立。
又因为 A X = b , A y = b AX=b,Ay=b AX=b,Ay=b,那么 y = X + v , v ∈ N ( A ) y=X+v,v\in \mathcal{N}(A) y=X+v,v∈N(A),即A的化零空间中的一个向量。
y是方程组的解,等于通解v加上特解X
因此,最优性条件可表示为
∇
f
0
(
x
)
v
≥
0
,
∀
v
∈
N
(
A
)
\nabla f_0(x)v\geq 0,\forall v\in \mathcal N(A)
∇f0(x)v≥0,∀v∈N(A)
那么只有两种情况:
-
子空间退化为零点:那么 y = = X y==X y==X,即方程只有一个解,矩阵A是可逆的。
-
∇ f 0 ( x ) \nabla f_0(x) ∇f0(x)正交于子空间:
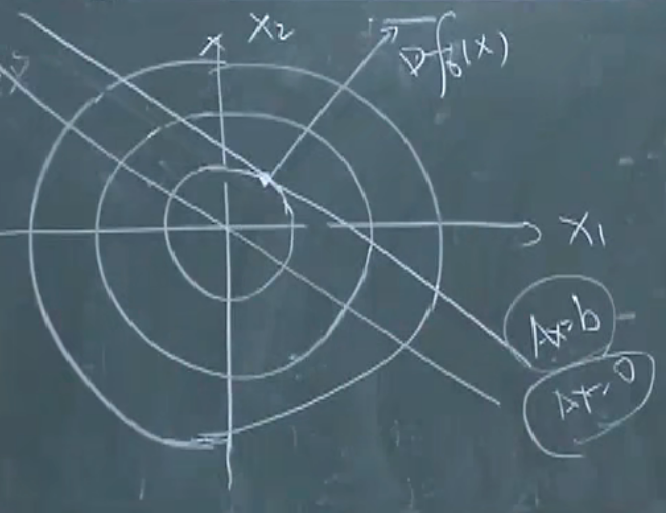
约束仅为非负约束:互补条件
min f 0 ( x ) s . t . x ≥ 0 \min f_0(x)\\ s.t.x\geq 0 minf0(x)s.t.x≥0
若
∃
x
≥
0
\exist x\geq 0
∃x≥0,
x
x
x最优等价于
∀
y
≥
0
\forall y\geq 0
∀y≥0
∇
f
0
T
(
x
)
(
y
−
x
)
≥
0
即
∇
f
0
T
(
x
)
y
−
∇
f
0
T
(
x
)
x
≥
0
\nabla f_0^T(x)(y-x)\geq 0\\ 即\nabla f_0^T(x)y-\nabla f_0^T(x)x\geq 0
∇f0T(x)(y−x)≥0即∇f0T(x)y−∇f0T(x)x≥0
- ①:若 ∇ f 0 T ( x ) ≤ 0 \nabla f_0^T(x)\leq 0 ∇f0T(x)≤0,则 ∇ f 0 T ( x ) y \nabla f_0^T(x)y ∇f0T(x)y必可以取无穷小,则必有 ∇ f 0 ( x ) ≥ 0 \nabla f_0(x)\geq 0 ∇f0(x)≥0
- ② ∀ y \forall y ∀y均有 ∇ f 0 ( x ) T ( y − x ) ≥ 0 \nabla f_0(x)^T(y-x)\geq 0 ∇f0(x)T(y−x)≥0,当y=0时, ∇ f 0 T ( x ) x ≤ 0 \nabla f_0^T(x)x\leq 0 ∇f0T(x)x≤0
- ③ ∇ f 0 T ( x ) ≥ 0 , x ≥ 0 , \nabla f_0^T(x)\geq 0,x\geq 0, ∇f0T(x)≥0,x≥0,则 ∇ f 0 T ( x ) x ≥ 0 \nabla f_0^T(x)x\geq 0 ∇f0T(x)x≥0
由②和③可知, f 0 T ( x ) x = 0 f_0^T(x)x=0 f0T(x)x=0
结论:如果x是最优解,那么一定满足下面的条件
{
x
≥
0
∇
f
0
(
x
)
≥
0
(
∇
f
0
(
x
)
)
i
x
i
=
0
\begin{cases}x\geq 0\\ \nabla f_0(x)\geq 0\\ (\nabla f_0(x))_ix_i=0\end{cases}
⎩
⎨
⎧x≥0∇f0(x)≥0(∇f0(x))ixi=0
该条件称为互补条件。
几何解释: