TOPSIS法是一种常用的综合评价方法，能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距。

基本过程为先将原始数据矩阵统一指标类型（一般正向化处理）得到正向化的矩阵，再对正向化的矩阵进行标准化处理以消除各指标量纲的影响，并找到有限方案中的最优方案和最劣方案，然后分别计算各评价对象与最优方案和最劣方案间的距离，获得各评价对象与最优方案的相对接近程度，以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制，数据计算简单易行。即：

1. 将原始矩阵正向化，主要原始是指标评价的维度不同
2. 正向化矩阵标准化，消除量纲影响
3. 计算得分并归一化，

0. 引入

层次分析法个人感觉不合理之处有以下几点😂：

• 判断矩阵的构建依赖个人或者专家经验
• 考虑的指标可能不足，但又不能太多

1. 指标类型

极大型指标：越大越好

$$\frac{x-min}{max-min}$$

极小型指标：越小越好

转化为极大型指标：$$max-x$$

中间型指标：接近某个值最好，如pH

M = m a x { ∣ x i − x b e s t ∣ } M=max \{ |x_i - x_{best} |\} M=max{∣xi​−xbest​∣}
$$\tilde{x}=1-\frac{|x_i-x_{best}|}{M}$$

区间型指标：指标值落在某个区间内最好，例如人的体温在36°～37°这个区间比较好

M = max ⁡ { a − min ⁡ { x i } , max ⁡ { x i } − b } , x ~ i = { 1 − a − x i M , x i < a 1 , a ≤ x i ≤ b 1 − x i − b M , x i > b \begin{aligned} & M=\max \left\{a-\min \left\{x_i\right\}, \max \left\{x_i\right\}-b\right\}, \tilde{x}_i= \begin{cases}1-\frac{a-x_i}{M}, & x_i<a \\ 1 & , a \leq x_i \leq b \\ 1-\frac{x_i-b}{M} & , x_i>b\end{cases} \end{aligned} ​M=max{a−min{xi​},max{xi​}−b},x~i​=⎩ ⎨ ⎧​1−Ma−xi​​,11−Mxi​−b​​xi​<a,a≤xi​≤b,xi​>b​​

2. 正向化矩阵

3. 计算得分

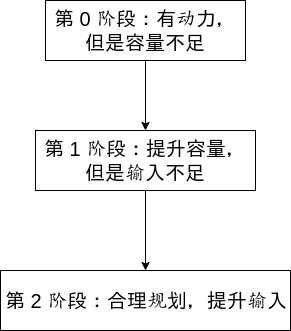
4. 流程图