文章目录
- 局部性原理
- 存储层次结构
- 存储层次结构示意图
- 传输数据示意图
- Cache 基础
- 映射方式
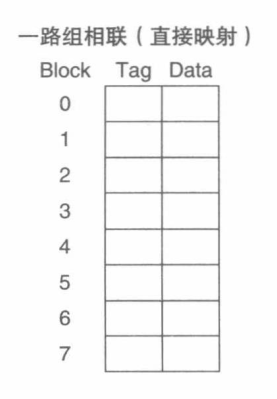
- 直接映射
- 全相连映射
- 组相连映射
- Cache 访问
- 直接映射
- 例题 —— Cache 容量计算
- 组相联映射
- 处理写操作
- 3C 模型
- Cache 失效问题 —— 通过更改 Cache 块容量,以此通过空间局部性来降低失效率
- Cache 性能
- Cache 可靠性
- 奇偶校验码
- 汉明纠错码
局部性原理

int num = 0;
for(int i = 1; i <= n; i++) {
num += i;
}
上面是个对 num 从 1 加到 10 的程序,使用 for 循环对 num 从 1 到 10 累加,需要访问 10 次,这便是时间局部性。
int A[10];
for(int i = 0; i < 10; i++) {
printf("%d ", A[i]);
}
上面是个遍历数组的程序,访问了 A[0],那么下一个就是访问 A[1],再下一个就是 A[2],以此类推,这便是空间局部性。
时间局部性 —— 若某个数据项被访问,那么在不久的将来它可能再次被访问。
空间局部性 —— 若某个数据项被访问,那么与它地址相邻的数据项也可能很快被访问。
存储层次结构

存储层次结构示意图
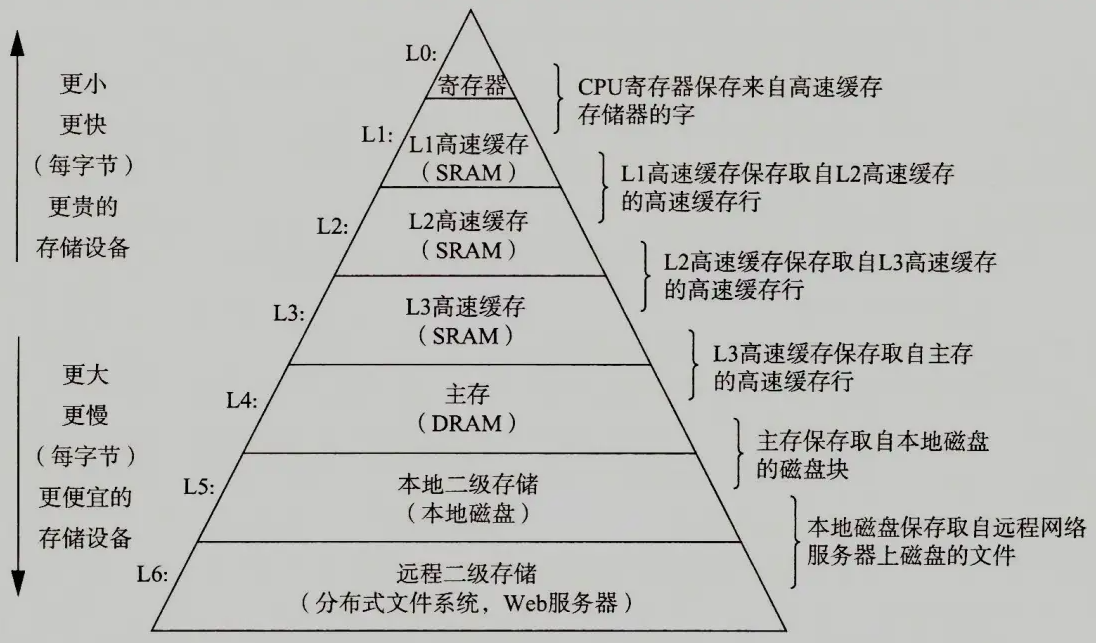
传输数据示意图
相邻层次之间进行数据传输时,传输单位的最小单位是块或行。
Cache 基础

映射方式
直接映射
直接映射: 基于内存块的地址来分配 Cache 中的位置。
由内存块地址映射到 Cache 块的公式:
内存块所对应的
C
a
c
h
e
块
=
(
内存块地址
)
m
o
d
(
C
a
c
h
e
中的块,即
C
a
c
h
e
块的数量
)
内存块所对应的Cache块 = (内存块地址) mod (Cache 中的块,即 Cache 块的数量)
内存块所对应的Cache块=(内存块地址)mod(Cache中的块,即Cache块的数量)
若 Cache 的块数是
2
n
2^n
2n,只需要取地址的低
N
N
N 位即可。其中
N
=
l
o
g
2
(
C
a
c
h
e
块数量
)
N=log_2(Cache 块数量)
N=log2(Cache块数量)。
由于一个 Cache 块可以保存不同的内存块,为了区分对应的实际是哪个,就引入了 Tag(标签),Tag 只需要保存地址的高位部分即可,这部分不会用来作为 Cache 索引,而是用于判断所请求的数据块是否在 Cache 中。
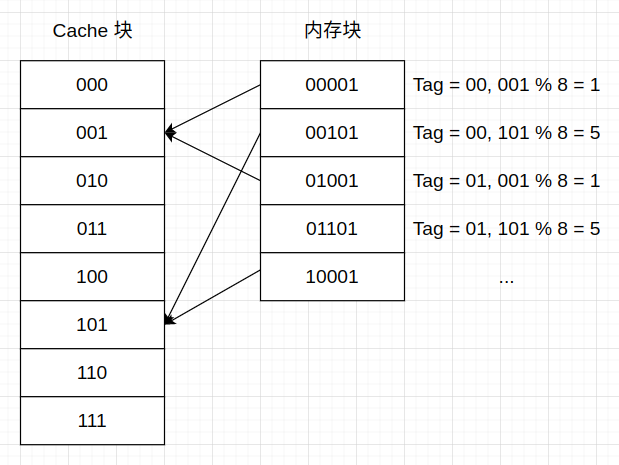
结构:
优点:
- 实现简单,硬件开销小。
缺点:
- 灵活性差:因为数据块所对应的 Cache 块是固定的,所以即便有多余的 Cache 空间那也用不了,因此会造成某个 Cache 块被频繁换进换出的情况。
- 适用与于大容量 Cache。
全相连映射

内存块可以选择任意一个 Cache 块,只要有空位就填上,也就是说数据块可以存放在 Cache 中的任意位置上。
优点:
- 灵活性:不需要做映射,只要看到有空位就直接填上。
缺点:
- 查询效率底下:当查找所需要的数据块所对应的 Cache 块时,必须从头到尾一个一个的 Tag 比较,因为数据块可以存放在任意位置。
- 硬件开销大:比较器增加了硬件开销。
- 只适合小容量的 Cache
组相连映射
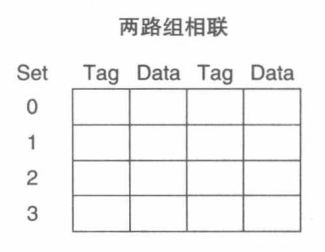
分成了若干的组(Set),每个组有 n n n 个位置,这样组成的结构称为 n n n 路组相联。内存块可放在某组中 n n n 个位置的任意位置。若要访问数据块所对应的 Cache 块,则需要在组中一个一个进行 Tag 比较。
计算内存块所对应的组号:
内存块所对应的组号
=
(
数据块号
)
m
o
d
(
C
a
c
h
e
中的组数
)
内存块所对应的组号=(数据块号)\ mod\ (Cache 中的组数)
内存块所对应的组号=(数据块号) mod (Cache中的组数)
Cache 的组数计算:
2
n
2^n
2n ,其中
n
n
n 便是低位的组索引。
优点与缺点: 组相联映射是结合了直接映射和全相联映射各自的优缺点给出的折中方案。
Cache 访问
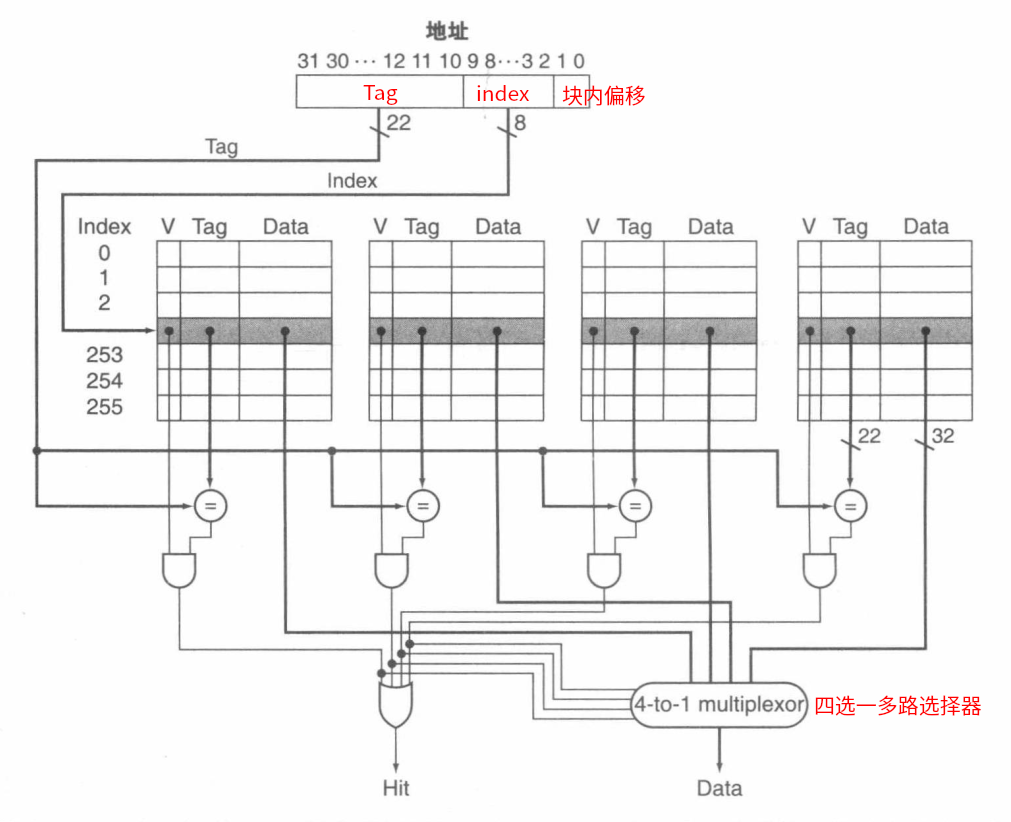
直接映射
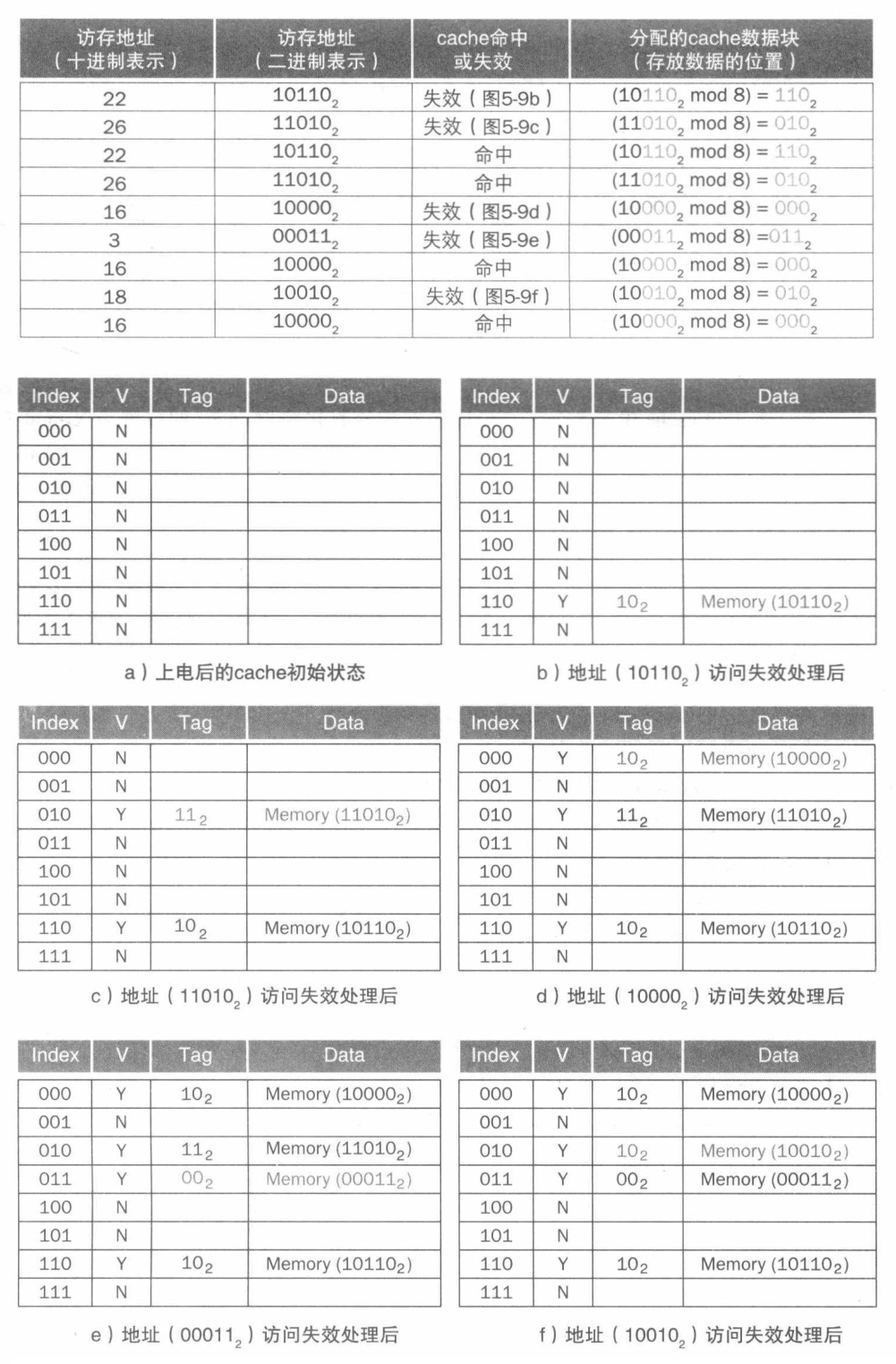
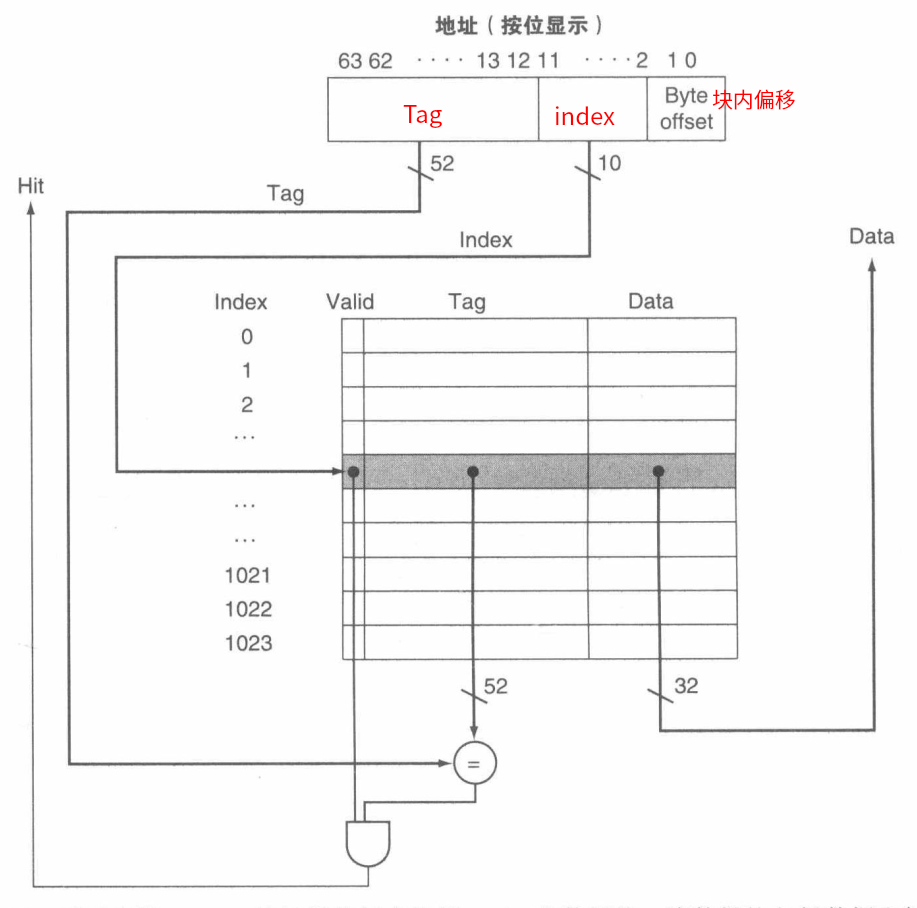
首先根据内存块地址的 Cache 块的 index 索引去寻找 Cache 块,找到后根据内存块的 Tag 去比较 Cache 中存储的 Tag 表项判断是不是需要请求的实际 Cache 块,若对上了就根据 Cache 块中 Data 表项存储的实际数据块(即内存块)的地址去得到访问数据。
**直接映射的 Cache 容量计算公式: **
2
n
×
(
单个数据块容量
+
标签字段大小
+
有效位大小
)
2^n \times (单个数据块容量 + 标签字段大小 + 有效位大小)
2n×(单个数据块容量+标签字段大小+有效位大小)
块内偏移量计算公式:
l
o
g
2
(
内存块大小,其单位为字节
)
log_2(内存块大小,其单位为字节)
log2(内存块大小,其单位为字节)
例题 —— Cache 容量计算
假设 64 位存储地址,对于直接映射 cache,如果数据大小为 16 Kib,每个数据块为 4 字大小。该 cache 容量多大(用 bit 表示)?
16K 是总的数据容量,我们需要分割这些容量,已知 16K 为 4096 个字,即 2 12 2^{12} 212。
因为单个数据块为 4 个字,因此共需要 4096 ÷ 4 = 1024 4096 \div 4 = 1024 4096÷4=1024 个数据块,即 2 10 2^{10} 210。
计算块内偏移: l o g 2 ( 4 字 ∗ 4 b y t e ) = l o g 2 ( 16 ) = 4 log_2(4字*4byte)=log_2(16)=4 log2(4字∗4byte)=log2(16)=4。
计算 Cacha 索引:因为总共需要 1024 个数据块,所以 l o g 2 ( 1024 ) = 10 log_2(1024)=10 log2(1024)=10。
计算标签: 64 − ( 10 + 4 ) = 50 64-(10+4)=50 64−(10+4)=50。
计算最终 Cache 容量:
2
10
×
(
4
×
32
+
50
+
1
)
=
2
10
×
179
=
179
K
i
b
2^{10} \times (4 \times 32 + 50 + 1) = 2^{10} \times 179 = 179 Kib
210×(4×32+50+1)=210×179=179Kib
组相联映射
处理写操作
写穿透(或写直达): 先将数据写入到 Cache 中,然后同时更新主存保持同步。
写缓冲: 一个保存等待写入主存的数据的队列。若写缓冲满了,处理器必须停顿流水线直到写缓冲中出现空闲表项目。若新数据产生的速度大于主存写的速率,那么多大的写缓冲容量都无济于事,因为写操作(即新数据产生或旧数据改变)的产生速度远远快于主存系统的处理速度。因此处理器通常会增多写缓冲的表项。
写返回: 数据只被写入到 Cache 中,被改写数据块在“替换出”Cache 时才被写到下一级存储。
3C 模型
- 强制失效(或冷启动失效) —— Cache 初始化,是首次访问的状态,首次访问必然失效。
- 容量失效 —— 当剩余的 Cache 容量不够程序执行所需时,处理器将部分块替换出去,空出来后让给程序使用。
- 冲突失效(或碰撞失效) —— 多个内存块同时竞争同一个 Cache 块,导致原本仍然需要的块被替换。
这里给出冲突失效的图示,便于理解,其它都挺好理解的。
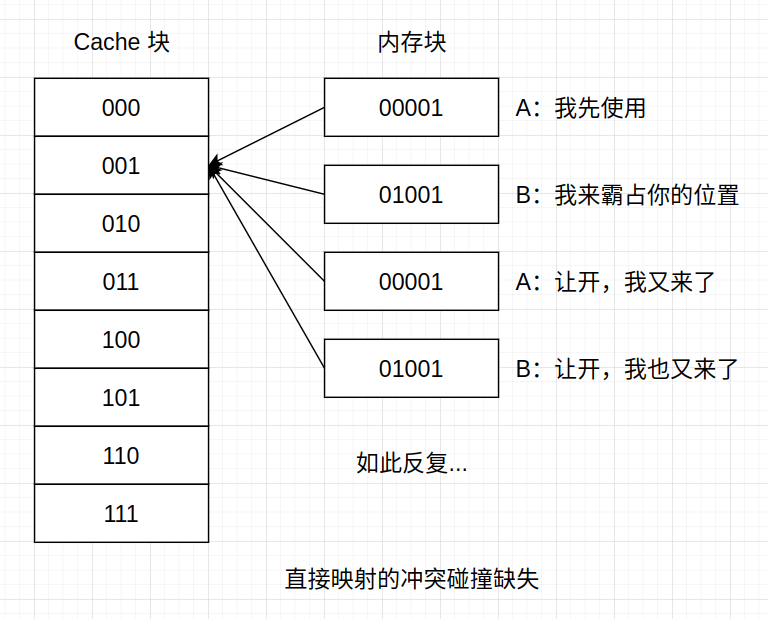
冲突碰撞缺失只对直接映射和组相联映射中有效,而全相联映射没有冲突碰撞缺失这种问题。
Cache 失效问题 —— 通过更改 Cache 块容量,以此通过空间局部性来降低失效率
假设一个 Cache 为 4 字节,有一个 32 字节长度的数组,每个元素占用 4 个字节。
现在要进行遍历数组操作,共需要访问 Cache 共 32 ÷ 4 = 8 32 \div 4 = 8 32÷4=8 次。
假设每个元素 16 字节,则需要访问 Cache 共 32 ÷ 16 = 2 32 \div 16 = 2 32÷16=2 次。
根据“空间局部性”可知每次有主存载入 Cache 时,也会载入其相邻的数据,因此缺失率就会降低。
因此 Cache 块越大,直接访问主存就越少,其访问 Cache 也会变少,但要知道从内存载入 Cache 可是很慢的,所以自然块越大所需要的载入时间越多。
Cache 性能
暂时忽略…(等我过几天回到学校后再补,我觉得这部分内容或许另一本书写的更好点)
Cache 可靠性
奇偶校验码
汉明距离: 两个等长二进制对应位置不同的位的数量。例如 011011 和 001111 的距离为 2,因为从左至右进行逐位比较出 2 位不同,这也称为码距。
奇偶校验位:
- 奇校验码:0 表示奇数,1 表示偶数。
- 偶校验码:0 表示偶数,1 表示奇数。
奇偶校验码: 是一种通过增加冗余位使得码字中"1"的个数恒为奇数或偶数的编码方法,它是一种检错码。
奇偶校验码原理:
- 奇校验码: 加上校验位后码长为 N 的码字中 1 的个数必须为奇数个,否则错误。
- 偶校验码: 加上校验位后码长为 N 的码字中 1 的个数必须为偶数个,否则错误。
例题: 求 1001101 和 1010111 的奇偶校验码,假设最高位为校验位。
1001101 的 1 个数为 4 个
1010111 的 1 个数为 5 个
求奇校验码:
_1001101 的校验位为 1,即 11001101
_1010111 的校验位为 0,即 01010111
假设 11001101 在传输过程中,数据没有发生错误。
统计 1 的个数为 5,符合奇校验码的校验原则,故而数据正确。
假设 11001101 在传输过程中,最低位发生了错误,导致数据变为 11001100。
统计 1 的个数为 4,不符合奇校验码的校验原则,故而数据错误,但无法得知具体错误位置。
求偶校验码:
_1001101 的校验位为 0,即 01001101
_1010111 的校验位为 1,即 11010111
假设 11010111 在传输过程中,最低位发生了错误,导致数据变为 11010110。
统计 1 的个数为 5,不符合偶校验码的校验原则,故而数据错误,但无法得知具体错误位置。
只能处理发生了一次错误的情况,若发生偶数次,则无法正确检测,例如 01010111 发生两次错误,数据为 010101[00],这个 1 个数还是奇数个,符合判定条件,会被误认为正确数据。
汉明纠错码
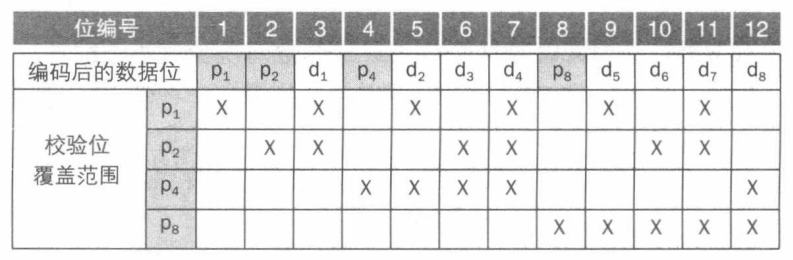
步骤:
- 从左至右由 1 开始依次编号。
- 将编号为 2 n 2^n 2n 的位标记为奇偶校验位。
- 剩余的全部用于数据位。
- 奇偶校验位的位置决定了其对应的数据位。
注意: 每个数据位都至少被两个奇偶校验位所覆盖。
如图所示:
例题: 码长为 8 的二进制数据为 10011010。求出对应的汉明纠错码,然后将第 10 位取反。
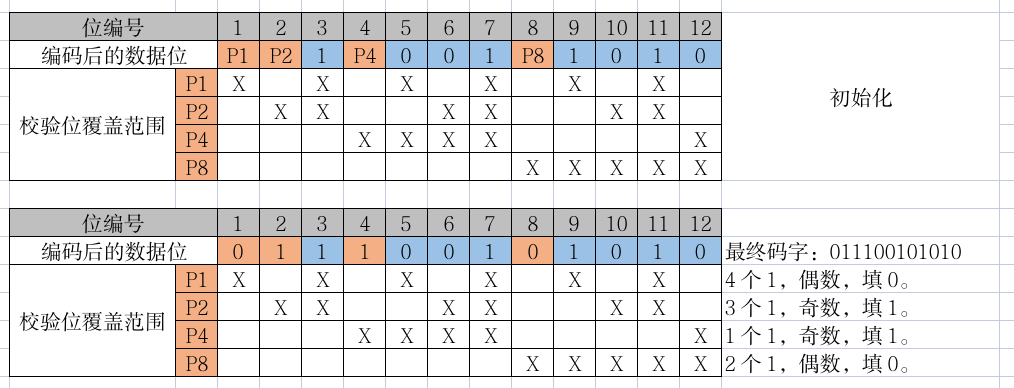
现在将第 10 位取反。

可以发现 P2 和 P8 校验位错误,因此 2 + 8 = 10 2+8=10 2+8=10,表示第 10 位数据错误,将其取反修正便得到正确答案。






![【C#】[带格式的字符串] 复合格式设置字符串与使用 $ 的字符串内插 | 如何格式化输出字符串](https://img-blog.csdnimg.cn/176899f47ce848d38989dff6fee5a0bb.png)