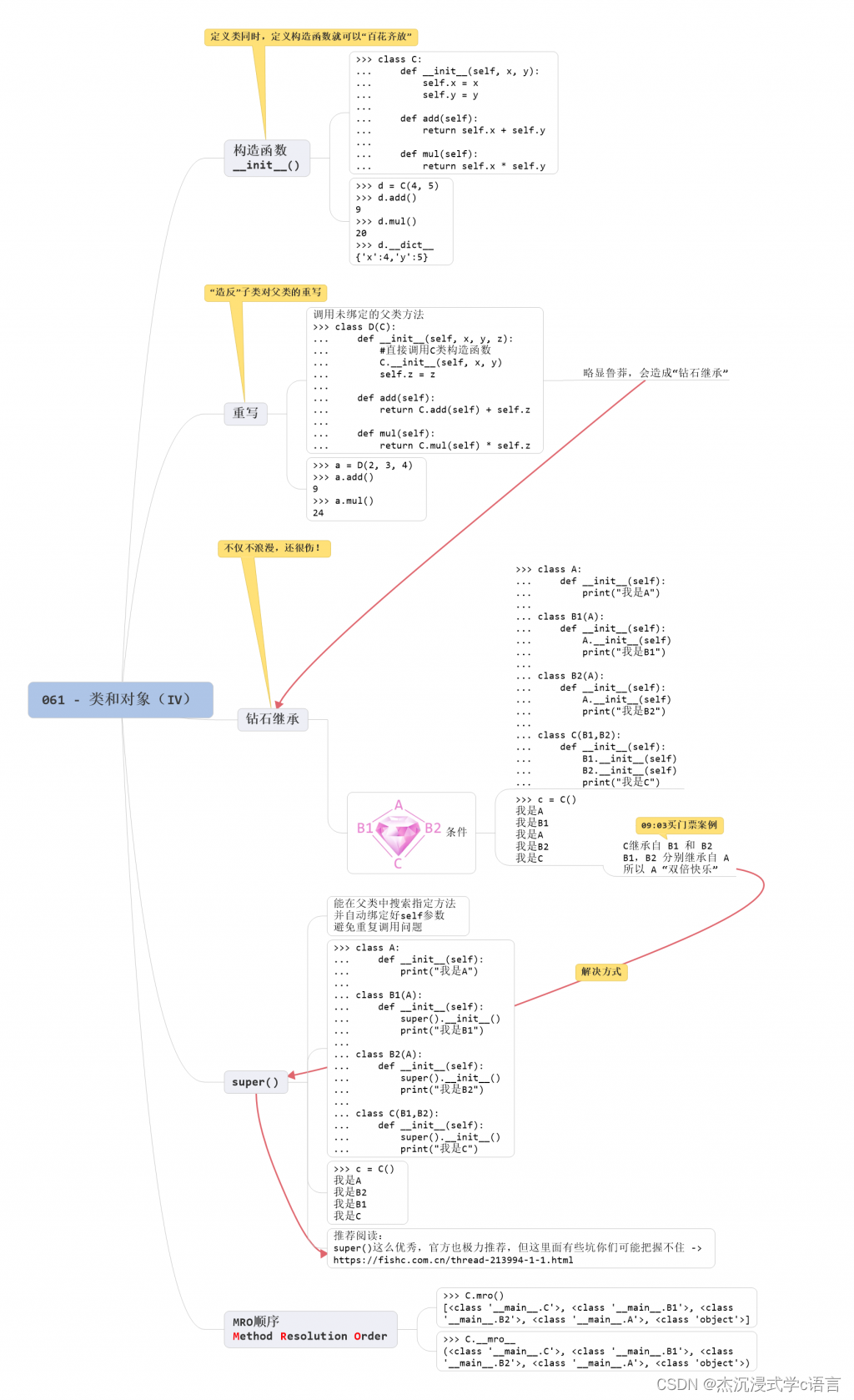
1. 构造函数（_ init _(self[,……])）

在类中定义 _init _() 方法，可以实现在实例化对象的时候进行个性化定制：

>>> class C:
...     def __init__(self, x, y):
...         self.x = x
...         self.y = y
...     def add(self):
...         return self.x + self.y
...     def mul(self):
...         return self.x * self.y
...        
>>> c = C(2, 3)
>>> c.add()
5
>>> c.mul()
6

2.重写

前面我们在 “继承” 中讲过，如果对于父类的某个属性或方法不满意的话，完全可以重新写一个同名的属性或方法对其进行覆盖。那么这种行为，我们就称之为是子类对父类的重写。

这里，我们可以定义一个新的类 —— D，继承自上面的类 C，然后对 add() 和 mul() 方法进行重写：

>>> class D(C):
...     def __init__(self, x, y, z):
...         C.__init__(self, x, y)
...         self.z = z
...     def add(self):
...         return C.add(self) + self.z
...     def mul(self):
...         return C.mul(self) * self.z
...
>>> d = D(2, 3, 4)
>>> d.add()
9
>>> d.mul()
24

3.砖石继承

下面代码中，类 B1 和类 B2 都是继承自同一个父类 A，而类 C 又同时继承自它们，这种继承模式就被称之为钻石继承，或者菱形继承：

>>> class A:
...     def __init__(self):
...         print("哈喽，我是A~")
...
>>> class B1(A):
...     def __init__(self):
...        A.__init__(self)
...        print("哈喽，我是B1~")
...
>>> class B2(A):
...     def __init__(self):
...         A.__init__(self)
...         print("哈喽，我是B2~")
...
>>> class C(B1, B2):
...     def __init__(self):
...         B1.__init__(self)
...         B2.__init__(self)
...         print("哈喽，我是C~")
...

钻石继承这种模式，一旦处理不好就容易带来问题：

>>> c = C()
哈喽，我是A~
哈喽，我是B1~
哈喽，我是A~
哈喽，我是B2~
哈喽，我是C~

看，“哈喽，我是A~” 这一句竟然打印了 2 次！

也就是说，类 A 的构造函数被调用了 2 次！

怎么解？

看下面~

4.supper（）函数和MRO顺序

上面这种通过类名直接访问的做法，是有一个名字的，叫 “调用未绑定的父类方法”。

通常使用其实没有多大问题，但是遇到钻石继承嘛，就容易出事儿了~

那么其实 Python 还有一个更好的实现方案，就是使用 super() 函数。

super() 函数能够在父类中搜索指定的方法，并自动绑定好 self 参数。

>>> class B1(A):
...     def __init__(self):
...        super().__init__()
...        print("哈喽，我是B1~")
...
>>> class B2(A):
...     def __init__(self):
...         super().__init__()
...         print("哈喽，我是B2~")
...
>>> class C(B1, B2):
...     def __init__(self):
...         super().__init__()
...         print("哈喽，我是C~")
...
>>> c = C()
哈喽，我是A~
哈喽，我是B2~
哈喽，我是B1~
哈喽，我是C~

之所以 super() 函数能够有效避免钻石继承带来的问题，是因为它是按照 MRO 顺序去搜索方法，并且自动避免重复调用的问题。

那什么是 MRO 顺序呢？

MRO（Method Resolution Order），翻译过来就是 “方法解析顺序”。

想要查找一个类的 MRO 顺序有两种方法~

一种是通过调用类的 mro() 方法：

>>> C.mro()
[<class '__main__.C'>, <class '__main__.B1'>, <class '__main__.B2'>, <class '__main__.A'>, <class 'object'>]
>>> B1.mro()
[<class '__main__.B1'>, <class '__main__.A'>, <class 'object'>]

另一种则是通过 mro 属性：

>>> C.__mro__
(<class '__main__.C'>, <class '__main__.B1'>, <class '__main__.B2'>, <class '__main__.A'>, <class 'object'>)
>>> B2.__mro__
(<class '__main__.B2'>, <class '__main__.A'>, <class 'object'>)