前置问题

问题解答

一、基础概念：最小生成树的定义和性质

（1）最小生成树（Minimal Spanning Tree）的定义

• 生成树的代价：设$G(V,E)$是一个无向连通网图，生成树上各边的权值之和称为生成树的代价。
• 最小生成树：在图$G$所有生成树中，代价最小的生成树为最小生成树。

（2）最小生成树（MST）的性质

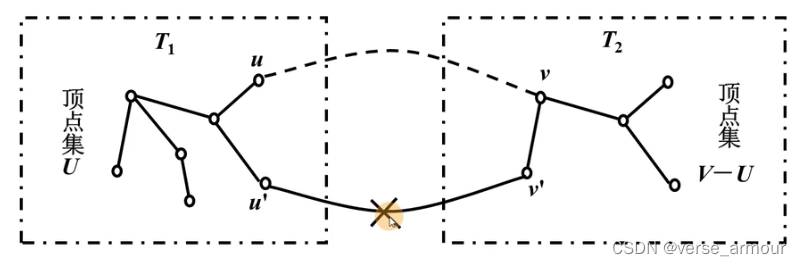
假设$G=(V,E)$是一个无向连通网图，$U$是顶点集的一个非空子集。若$(u,v)$是一条具有最小权值的边，其中$u\in U,v\in V-U$,则必存在一棵包含边$u,v$的最小生成树。

二、如何利用MST性质寻找最小生成树

• 找到两个点集之间最小权值的边$(u,v)$，让具有最小权值的$(u,v)$成为最小生成树的一部分，将大于最小权值的$(u,v)$删除。

接下来有两个思路：

• 从一个点出发，一次加入点形成点集（Prim算法）
• 从边出发，将点集合并，避免形成环（Kruskal算法）

三、Prim算法

（1）Prim算法思想

对点做操作，维护一个在最小生成树中的点的顶点集A，以及一个待处理点的顶点集B，每次找出连接这两个集合的最短边，并将其两个顶点都加入集合A，直到所有顶点都处理完毕。

抽象描述：（觉得抽象跳过）

（2）Prim算法形成最小生成树的详细过程

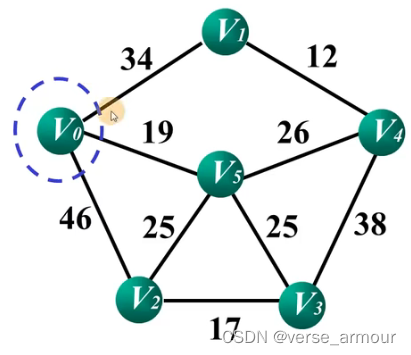
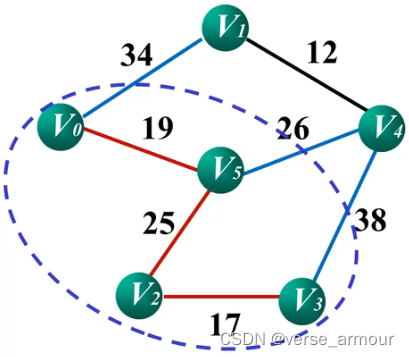
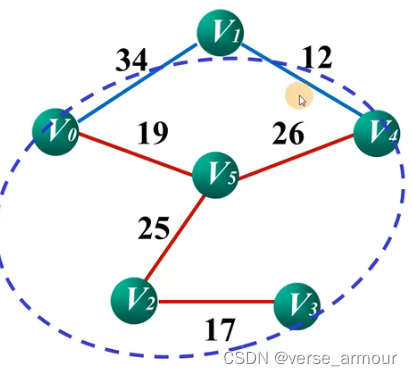
图注：

• 红色线段表示最小生成树
• 蓝圈表示集合$U$，其他顶点集合为$V-U$
• 蓝色线段表示$U$和$V-U$的相邻边

$计算U中每个点和其相邻点之间的代价，找出代价最小的点V5，将V5纳入U集合。$

---

---

---

---

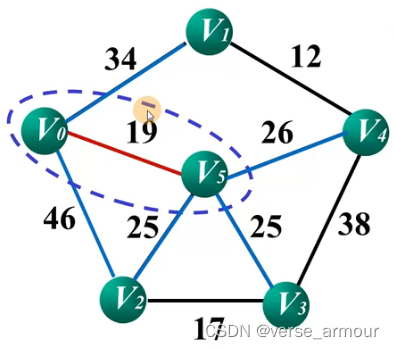
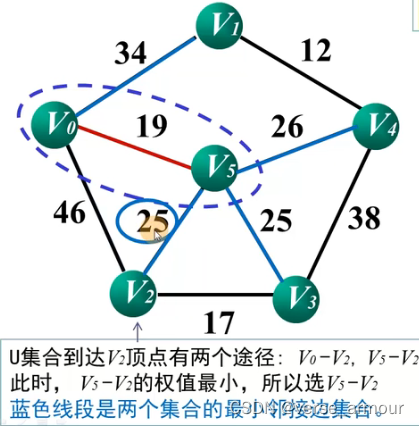
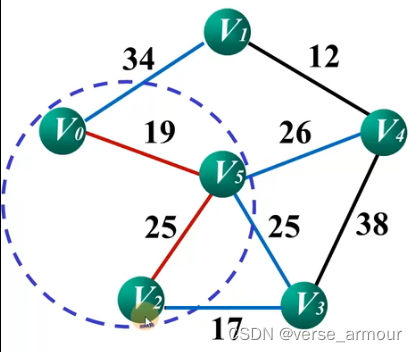
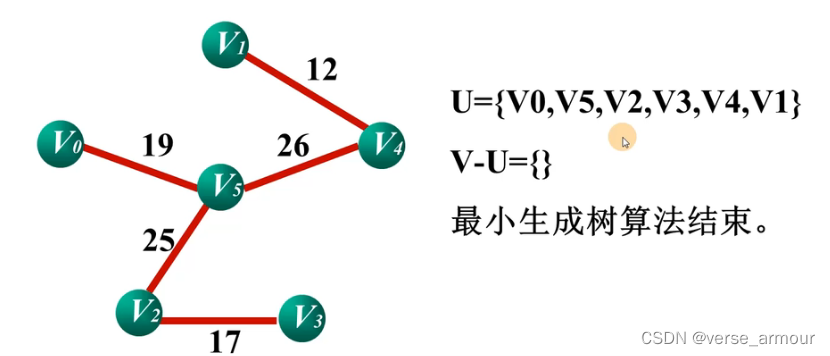
（3）Prim算法的C++和python实现

四、Dijkstra算法

（1）和Prim算法的联系

Dijkstra算法和Prim算法都是最短路径算法，主要用于求图的最短路径。

不同点在于，Dijkstra算法适用于有向图起点到其他点的最短路径，而Prim算法适用于无向图求最小生成树。它们的求解过程也略有不同。Dijkstra算法每次选择距离起点最近的点作为新的访问点，更新其他点到起点的最短距离，直到所有点都被访问。Prim算法则从一个起点开始，不断选择与已经访问过的点相连且边权最小的点，直到图上所有点都被访问。

（2）Dijkstra算法思想

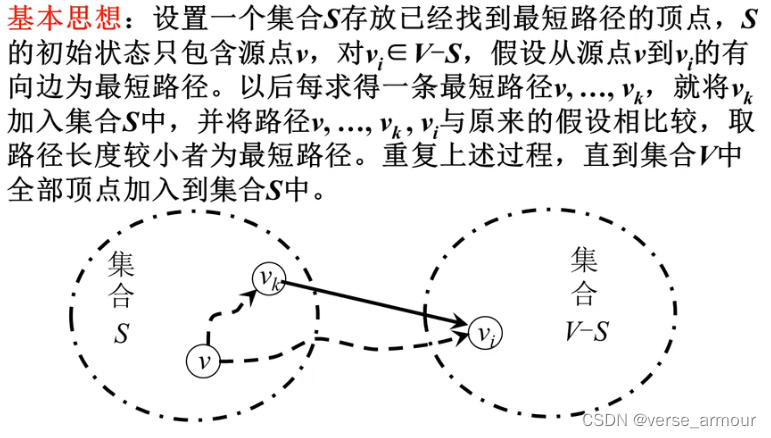
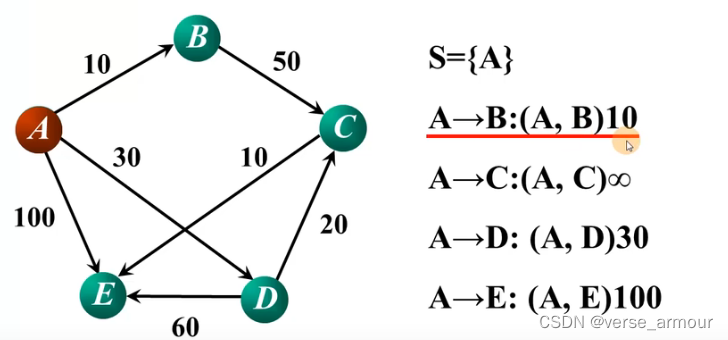
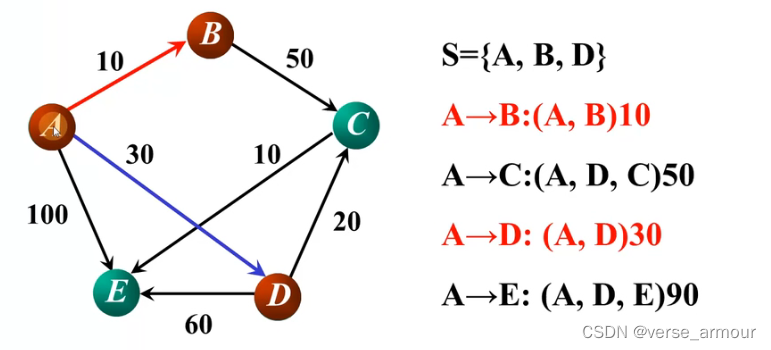
算出A点到图中每一点的路径长度，选出一条最短路径：A->B，将顶点B加入集合S。

增加了一条最短路径之后，顶点A到其他点的路径是不是有更短的路径了呢？

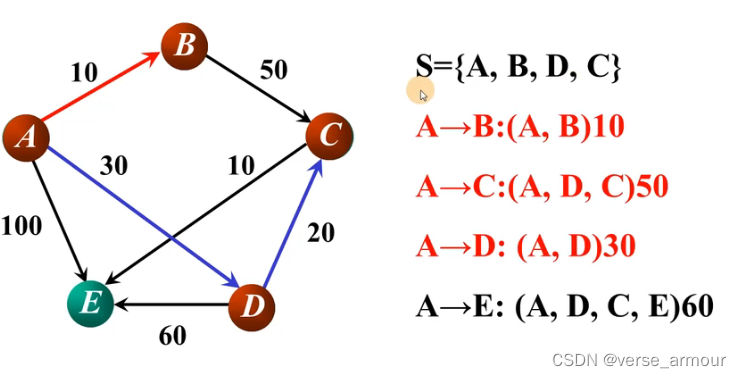
更新最短路径：

---

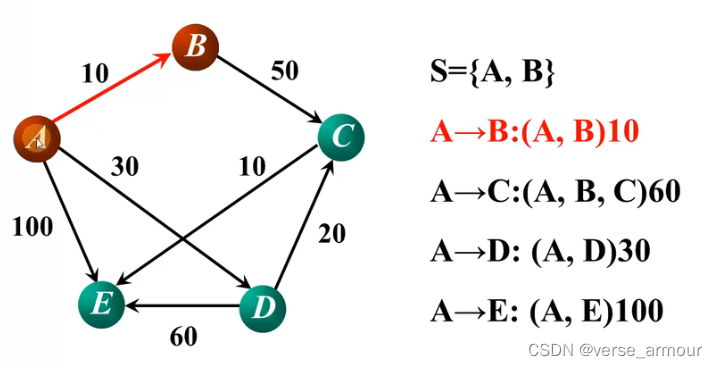
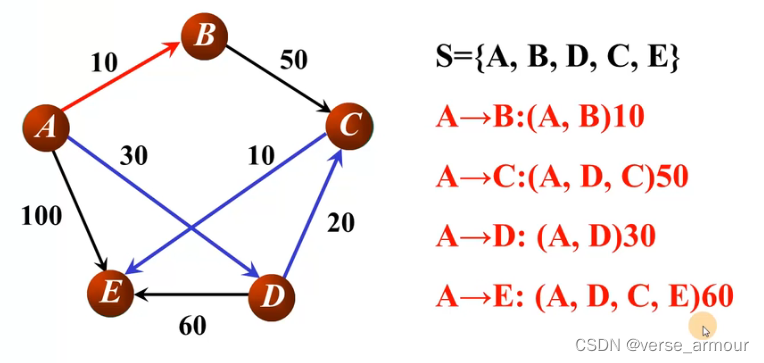
在A->C,A->D,A->E中选出最短路径：A->D，并将D顶点加入S集合。更新所有最短路径。

---

---