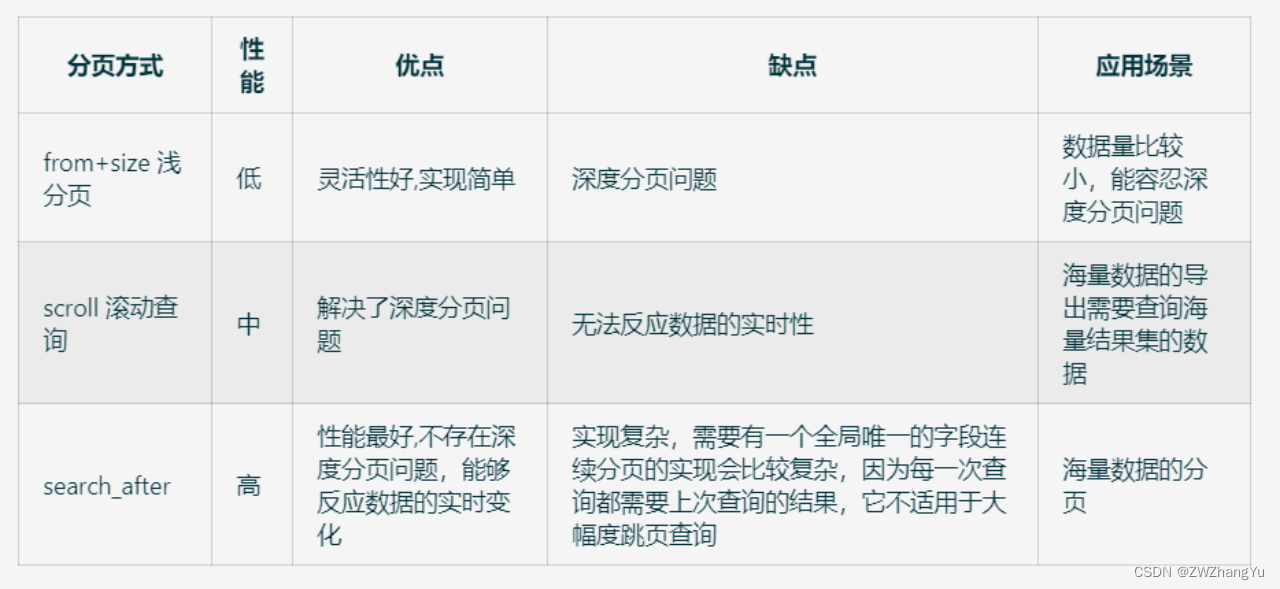
主页:114514的代码大冒险
qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ )
Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com
引入
我们之前已经学过线性数据结构,今天我们将介绍非线性数据结构----树
望文生义,这个数据结构肯定与现实中的树, 有着一定的联系,如图:

数据结构中的树它看起来像树枝,也想树的根部
树的概念

树的相关概念
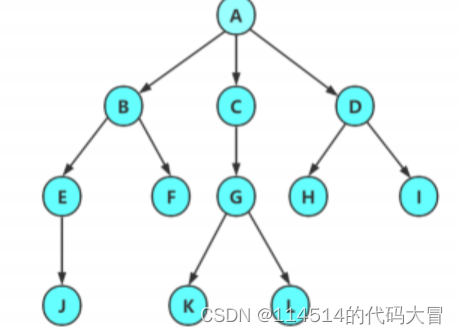
节点的度 :一个节点含有的子树的个数称为该节点的度;如上图: A 的为 6叶节点或终端节点 :度为 0 的节点称为叶节点;如上图: B 、 C 、 H 、 I... 等节点为叶节点非终端节点或分支节点 :度不为 0 的节点;如上图: D 、 E 、 F 、 G... 等节点为分支节点双亲节点或父节点 :若一个节点含有子节点,则这个节点称为其子节点的父节点;如上图: A 是 B 的父节点孩子节点或子节点 :一个节点含有的子树的根节点称为该节点的子节点;如上图: B 是 A 的孩子节点兄弟节点 :具有相同父节点的节点互称为兄弟节点;如上图: B 、 C 是兄弟节点树的度 :一棵树中,最大的节点的度称为树的度;如上图:树的度为 6节点的层次 :从根开始定义起,根为第 1 层,根的子节点为第 2 层,以此类推;树的高度或深度 :树中节点的最大层次;如上图:树的高度为 4堂兄弟节点 :双亲在同一层的节点互为堂兄弟;如上图: H 、 I 互为兄弟节点节点的祖先 :从根到该节点所经分支上的所有节点;如上图: A 是所有节点的祖先子孙 :以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是 A 的子孙森林 :由 m ( m>0 )棵互不相交的树的集合称为森林;
树的表示
概念图:

树在实际中的运用(表示文件系统的目录树结构)
文件目录:

公司内部功能安排
二叉树(特殊的树)
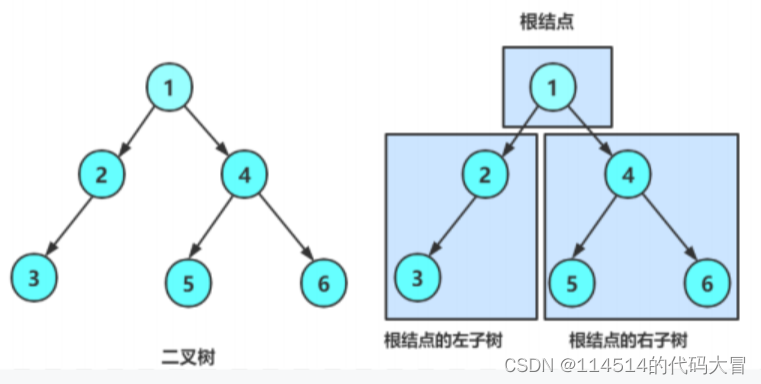
这些都不重要
你只需要知道二叉树的每个节点最多两个孩子
可以没有孩子,也可以只有一个孩子
另外在二叉树中
左孩子和右孩子是有差异的
现实中的二叉树


1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^k-1,则它就是满二叉树。
2. 完全二叉树 :完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K 的,有 n 个结点的二叉树,当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 1 至 n 的结点一一对 应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。
说人话:
就是说如果除了最底下那一排(所谓的叶子节点)其他的节点都有两个孩子
我们就称之为满二叉树

那么什么是完全二叉树呢
就是除了树的倒数第二排之外,其他节点都有两个孩子
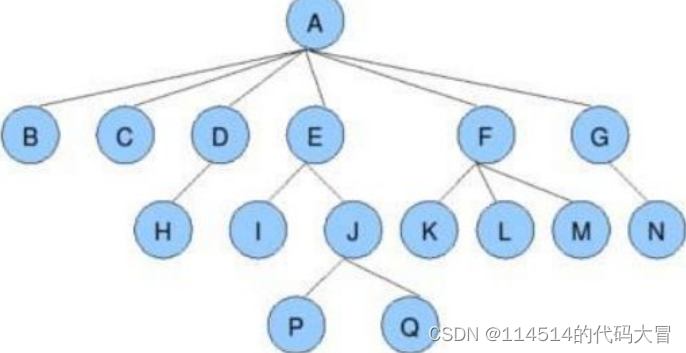
如图: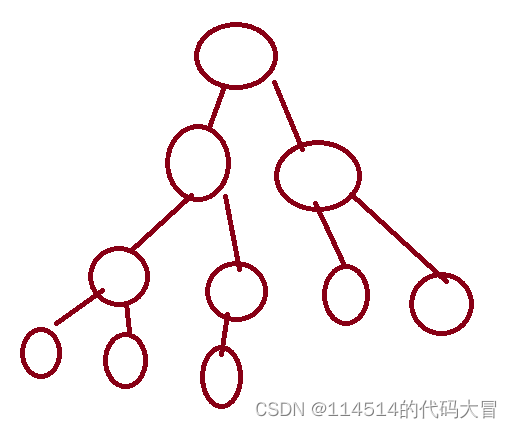
二叉树的性质


说了一大堆,能看懂多少算多少
我来说几个比较可能用到的点
 只要是树,有两个孩子的节点始终比没有孩子的节点的数量少一
只要是树,有两个孩子的节点始终比没有孩子的节点的数量少一
完全二叉树的坐标规律如右图所示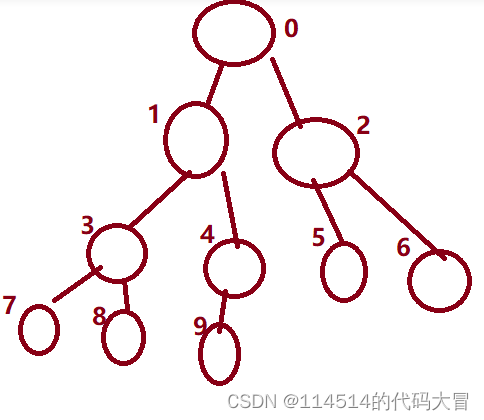
(完全二叉树中) 我们假使某节点这个下标为i,那么它的父亲就是
(i-1)/2 ,左孩子(如果有的话)为2*i+1,右孩子为左孩子坐标加1
另外还有就是这个完全二叉树的层数问题
除开最后一层外,第一层节点的数量为2^0,第二次为2^1第三次为2^2
第n层为2^(n-1),
如此满二叉树的节点数量为2^n - 1个
hhh,非满二叉树的节点数量则为前n-1层的节点数量+最后一层的节点数
我想,这个时候,在知道二叉树的节点的数量前提下
求出二叉树的深度,也就是层数不是什么困难的事情了
总结
这就是今天的树的概念讲解
这部分内容不需要太过焦虑
这些概念现在只是稍微有个大概就可以
我们在接下来的学习中会反复提到