1 背景

这篇短文的主要目的是去阐述“转方向盘”这一行为的基本性质：方向盘修正行为大致上服从一个方向盘转动速率的钟形曲线。（类似于reaching behavior如下图，所谓reahcing behavior，就是指人伸手去摸东西）

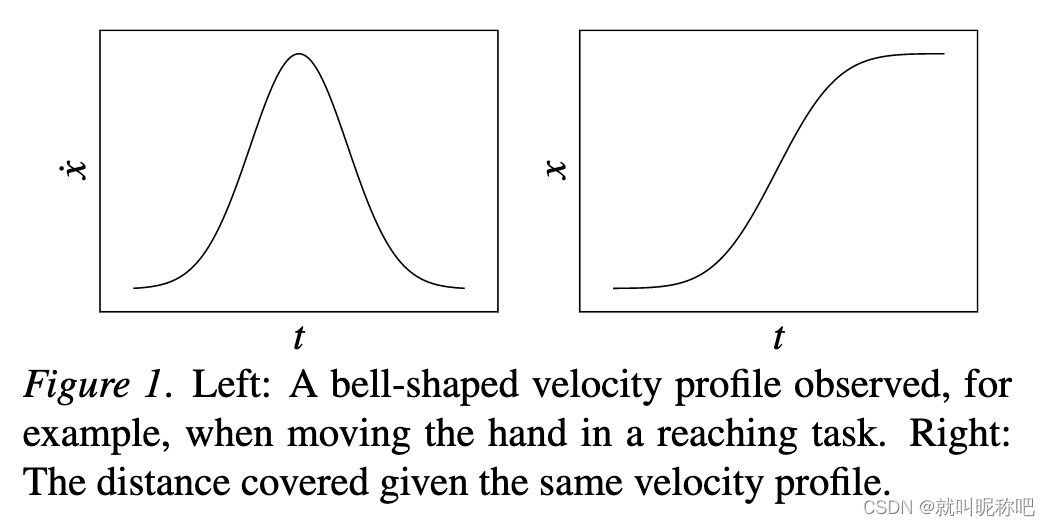
本文主要去探究以下3个问题：

方向盘修正行为是否也服从于一个钟形速率曲线？
方向盘转动速率和方向盘转角是否存在一个线性关系？这意味着方向盘修正的时间是个常量
复杂的方向盘转动行为是否可以由一些基本的行为元素组成？（motor primitives）

2 方法

本文只去探究方向盘的角度 $\delta(t)$ 和方向盘转动速率 $\dot{\delta}(t)$ 。如下图所示，可以看到， $\delta(t)$ 的单位是“角度”， $\dot{\delta}(t)$ 的单位是“角度/秒”。单个车的方向盘修正行为是从各种不同的数据集里面提取的。

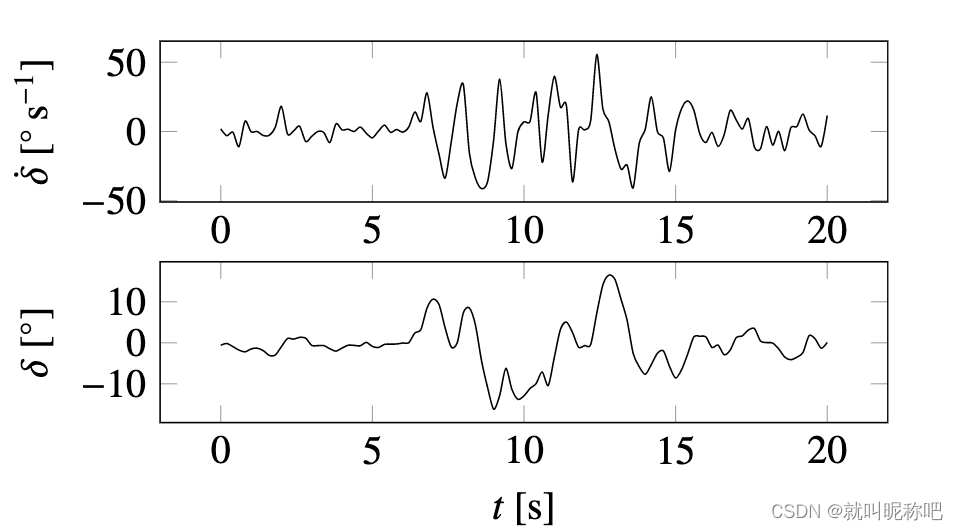
2.1 方向盘修正行为标识

为了识别方向盘的修正行为，需要用到一些常量（其实就是清洗数据的一些规则），如上面这个图。

方向盘开始转动时间 $t_0$ ：根据时间线，第一次满足不等式 $|\dot{\delta}(t)| \gt \dot{\delta}_{move}$ 的时间点
方向盘停止转动时间 $t_1$ ：方向盘开始转动后，第一次满足不等式 $|\dot{\delta}(t)| \lt \dot{\delta}_{still}$ （论文里这个不等式是大于号，但是我个人理解感觉应该是小于号）
最大方向盘转动速率： $\dot{\delta}_m = max(\{\dot{\delta}(t):t\in [t_0, t_1]\})$
整体的方向盘角度变化： $\Delta \delta = |\delta(t_0) - \delta(t_1)|$

应用上述规则去定义一个方向盘转动行为，还要额外考虑两条过滤规则，就是脏数据：

$\Delta \delta \lt \Delta \delta_{min}$
$max(\delta(t_0), \delta(t_1)) \gt \delta_{max}$

2.2 数据

数据集这方面，本文是选了6个数据来源，文中有进行一些简单介绍，这里就不记了，主要是想进行更完备的实验，得出更可靠的结论吧。

2.3 数据拟合

数据拟合就用高斯函数去做：

$\dot{\delta}(t) = \dot{\delta}_m exp(-\frac{(t-b)^2}{2\sigma^2})$

如果数据拟合完出来的函数， $R^2 \gt R_{fit}^2$ ，就认为符合钟形曲线。（ $\sigma$ 与方向盘修正持续时间密切相关）

3 结果

3.1 速率曲线

看下面这个图和表，就说绝大部分的这个方向盘修正行为都符合速率的钟形曲线，表的第二列代表的是每个数据集里可以被拟合成钟形的比率。这也回答了本文要探究的第一个问题。

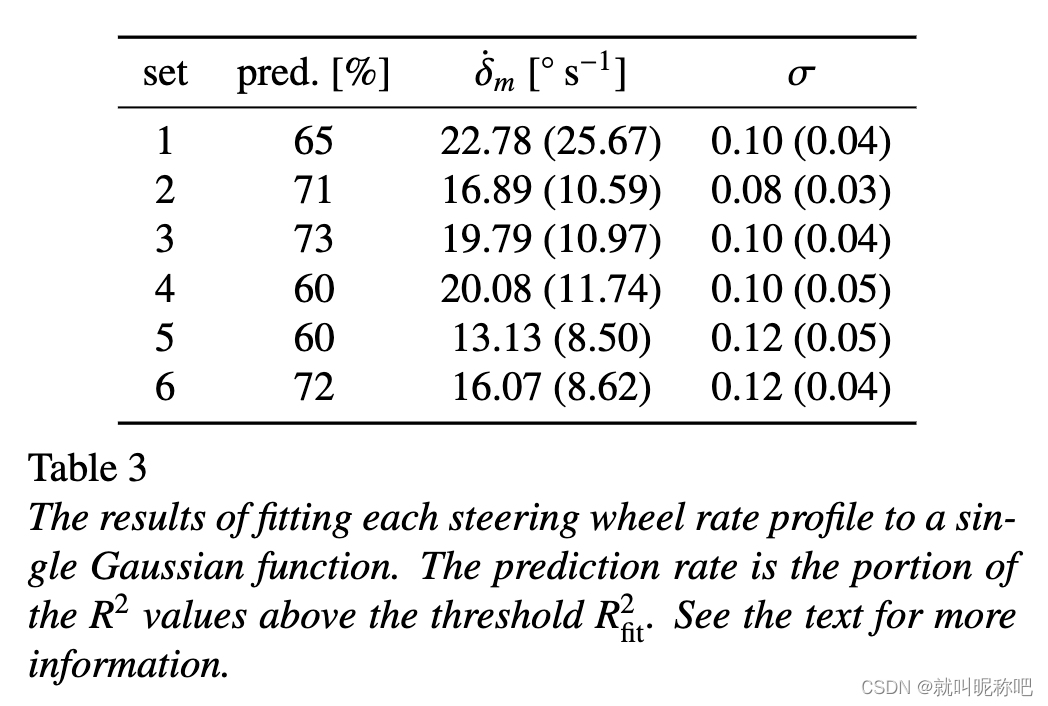
3.2 恒定的转向时间

从上面那个表里面可以看出， $\sigma$ 在不同数据集几乎是一样的，这意味着方向盘转动的持续时间基本都相同，下表的 $\Delta t$ 也指向相同结论。这意味着转向角和最大速率具有强烈的线性关系，从下表这个 $k$ 就可以看出来，另外去拟合线性关系也可以非常明显地看出这件事情，如下图。这回答了本文的第二个问题。

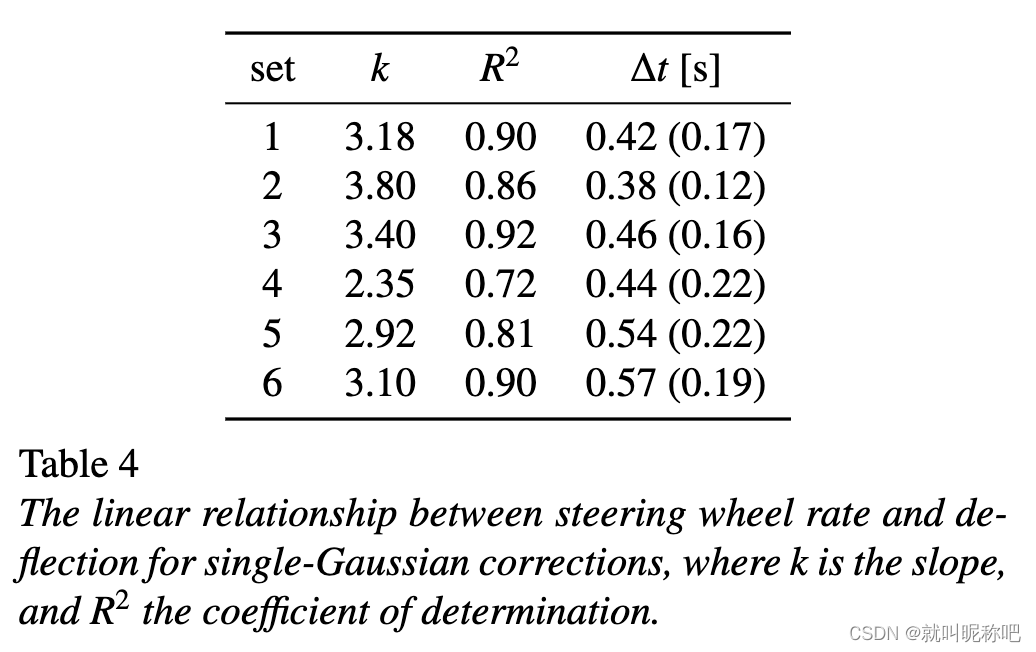
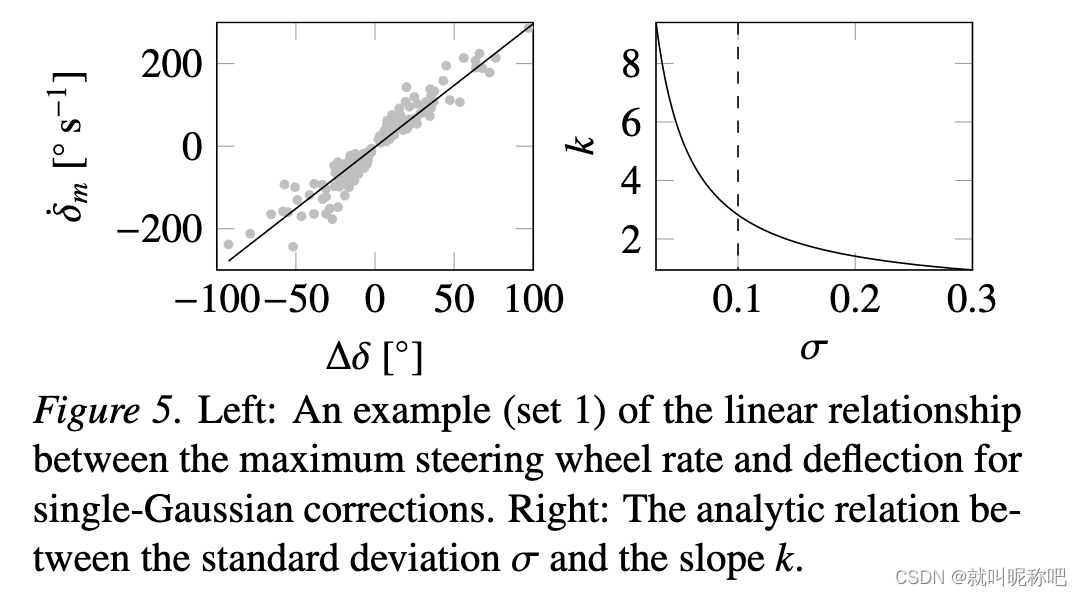
3.3 基本运动元素的叠加

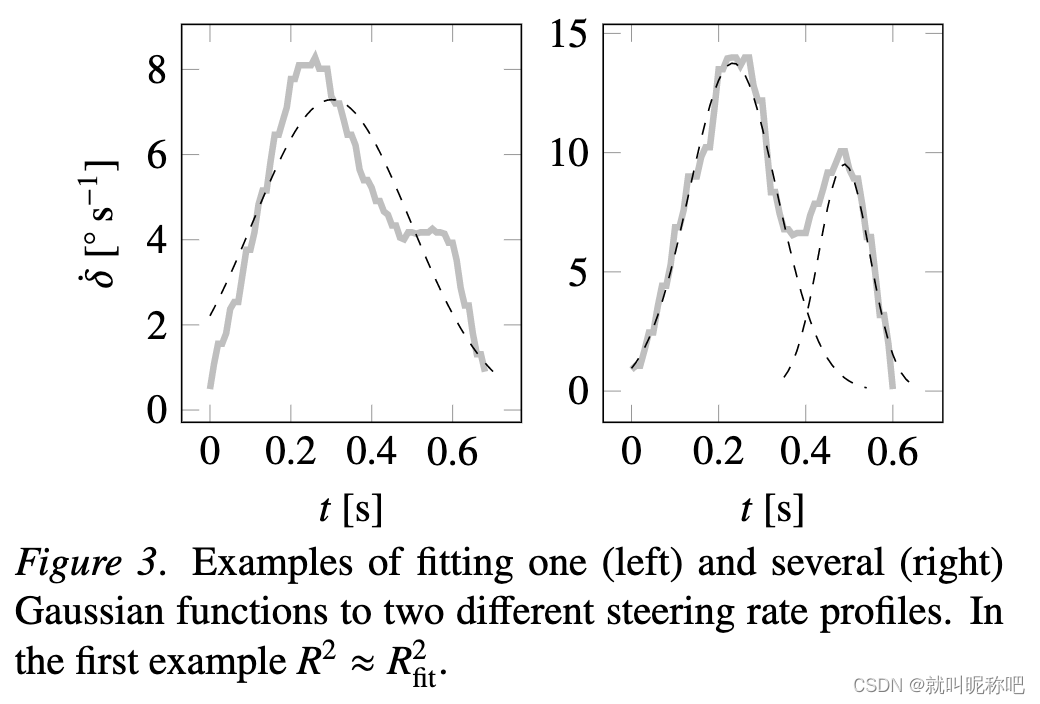
大多数的方向盘修正行为都可以被单个高斯函数拟合。对于那些拟合不好的，其实用多个高斯函数叠加去拟合也可以逐渐拟合成功，如下表所示，拟合标准还是 $R^2 \gt R_{fit}^2$ 。可以看到基本上两个就可以拟合绝大部分了。这回答了本文的第三个问题。

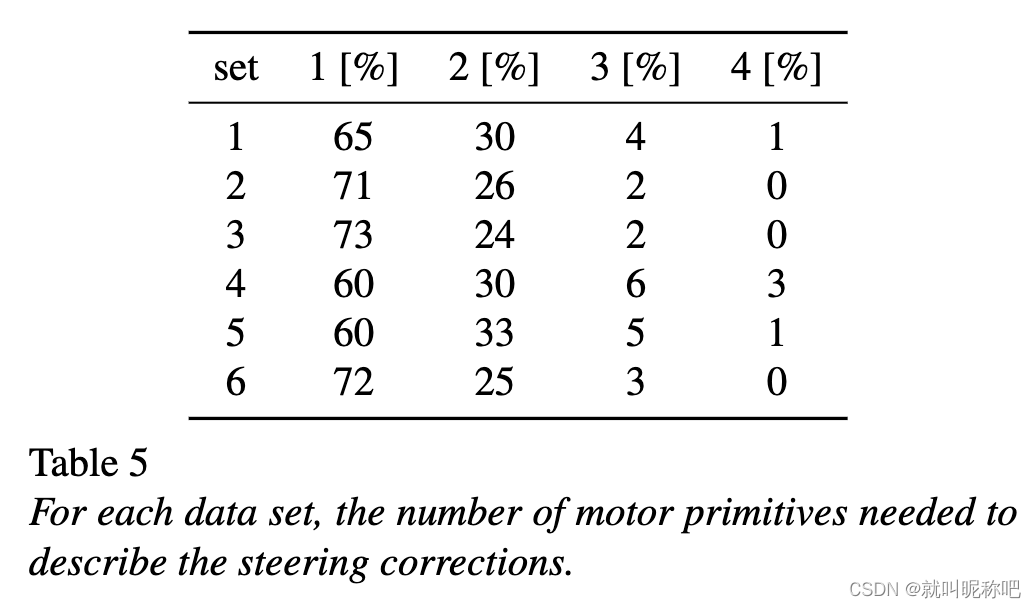
3.4 其他实验

为了让实验结论更有说服力，本文还做了点其他的实验，比如区分男女司机，区分年龄这种。得到的结果没区别。

4 讨论

既然发现了转角和最大速率的线性关系，那其实就可以这样搞：

$\Delta \delta = \int \dot{\delta}(t)dt = 2\dot{\delta}_m\sigma \sqrt{\pi}\\ \dot{\delta}_m= \frac{\Delta \delta}{2\sigma \sqrt{\pi}} = k\Delta \delta\\ k = \frac{1}{2\sigma \sqrt{\pi}}$