目录
题目描述
解析
解题思路
代码部分
代码部分
运行结果
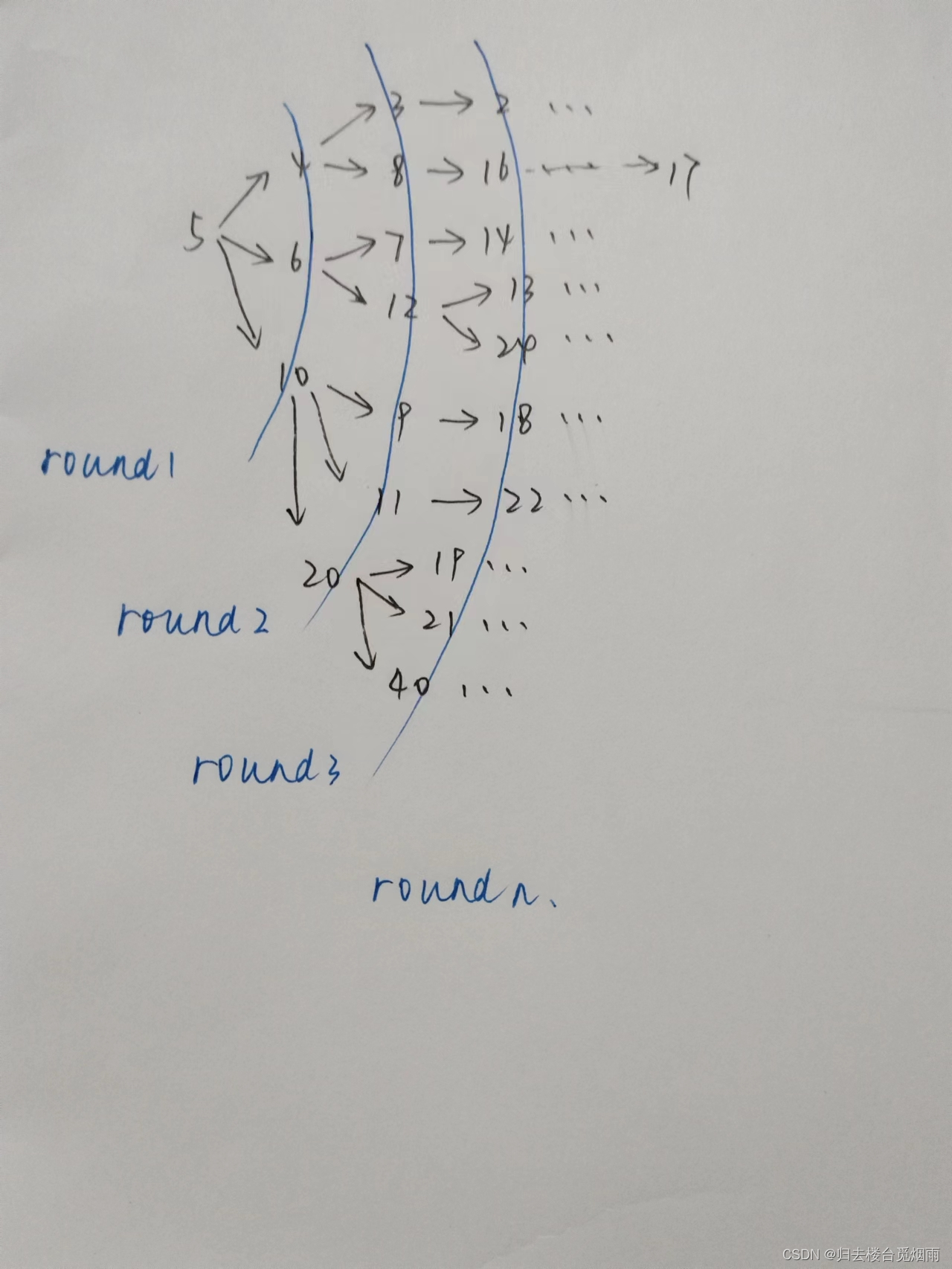
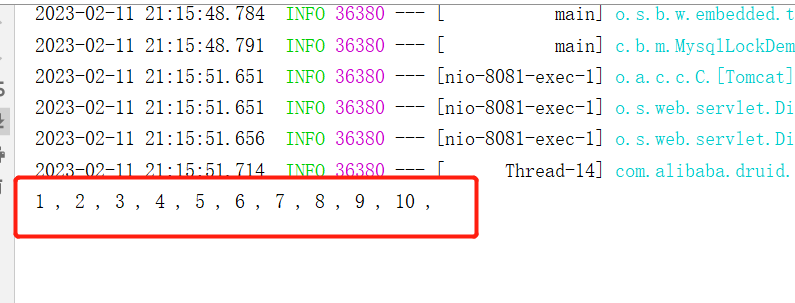
看看len数组中各个位置的标记值
为什么这样做一定是最短路径:
题目描述
农夫知道一头牛的位置,想要抓住它。农夫和牛都位于数轴上,农夫起始位于点N(0<=N<=100000),牛位于点K(0<=K<=100000)。农夫有两种移动方式:
1.从X移动到X-1或X+1,每次移动花费一分钟
2.从X移动到2*X,每次移动花费一分钟假设牛没有意识到农夫的行动,站在原地不动。
农夫最少要花多少时间才能抓住牛?
输入
两个整数,N和K。
输出
一个整数,农夫抓到牛所要花费的最小分钟数。
样例输入:
5 17样例输出:
4解析
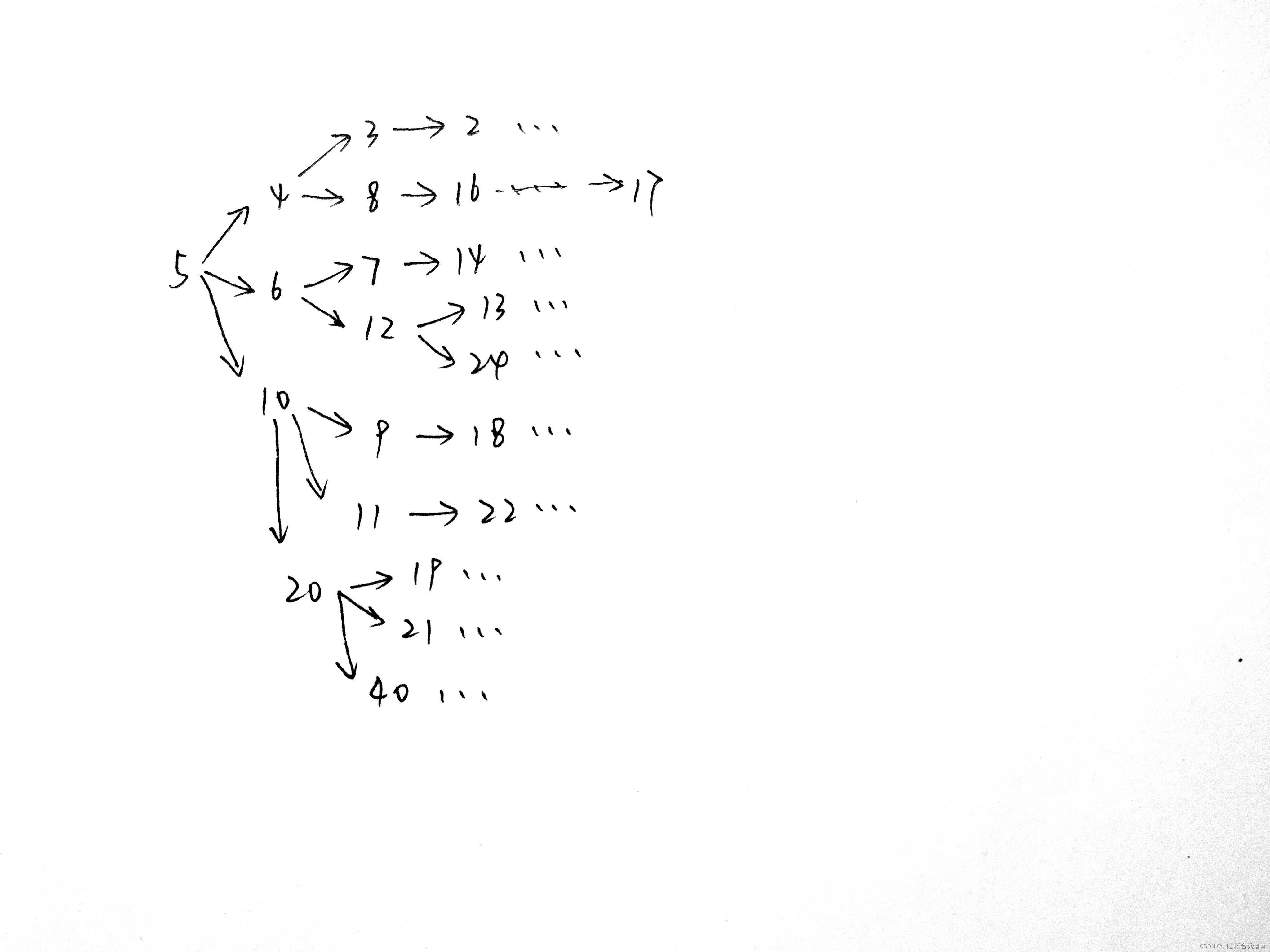
使用队列:
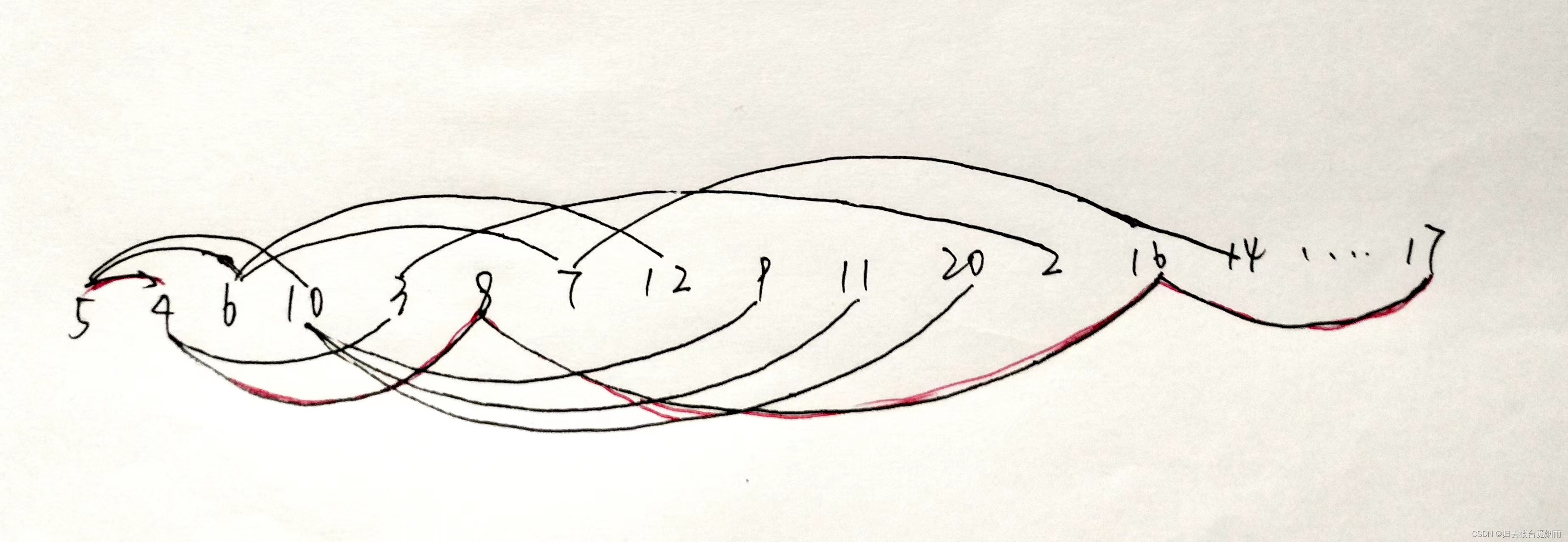
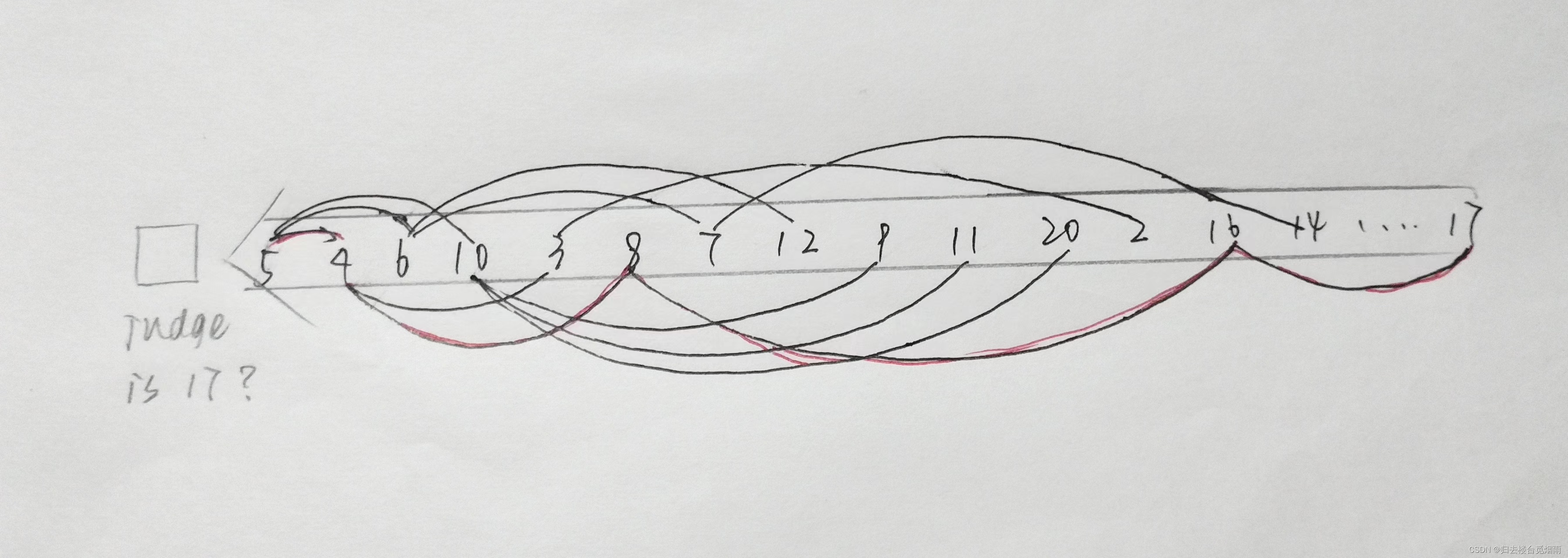
解题思路
使用队列从队尾依次传入值;判断队首值是否为所需值。
使用数组对每次将要传入的值做标记。从来没有传入过的值都标记为-1,传入且符合条件的,在上一次符合条件的标记值基础上加1。最终输出牛所在位置的标记值,即为运行了多少次。
代码部分
代码部分
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e5;
int len[N];//用于标记的数组定义
int main()
{
int n, k;
cin >> n >> k;
memset(len, -1, sizeof(len));//用于标记的数组初始化
//-1:从未进入过队列; 非-1:既表示进入了队列,又表示最短路径中,已经走了第几步。
queue<int>q;
q.push(n);
len[n] = 0;//农夫所在的第一个位置,标记为最短路径中的第0步
int x;//记录队首值(为了书写方便)
int y[3];//从一个位置可能延伸出的3个子位置
while (!q.empty())
{
x = q.front();
if (x == k)break;//如果检索到牛的位置,停止循环
q.pop();//如果不是牛的位置,弹出队首元素
y[0] = x - 1;
y[1] = x + 1;
y[2] = 2 * x;
for(int i=0;i<3;i++)
if (y[i] >= 0 && y[i] < N && len[y[i]] == -1)
//判断条件:如果该位置在数组界线内且从来没有进入过队列
{
q.push(y[i]);//让它进入队列
len[y[i]] = len[x] + 1;//又走了一步;
}
}
cout << len[k] << endl;
return 0;
}运行结果

看看len数组中各个位置的标记值
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e5;
int len[N];//用于标记的数组定义
int main()
{
int n, k;
cin >> n >> k;
memset(len, -1, sizeof(len));//用于标记的数组初始化
//-1:从未进入过队列; 非-1:既表示进入了队列,又表示最短路径中,已经走了第几步。
queue<int>q;
q.push(n);
len[n] = 0;//农夫所在的第一个位置,标记为最短路径中的第0步
int x;//记录队首值(为了书写方便)
int y[3];//从一个位置可能延伸出的3个子位置
while (!q.empty())
{
x = q.front();
if (x == k)break;//如果检索到牛的位置,停止循环
q.pop();//如果不是牛的位置,弹出队首元素
y[0] = x - 1;
y[1] = x + 1;
y[2] = 2 * x;
for(int i=0;i<3;i++)
if (y[i] >= 0 && y[i] < N && len[y[i]] == -1)
//判断条件:如果该位置在数组界线内且从来没有进入过队列
{
q.push(y[i]);//让它进入队列
len[y[i]] = len[x] + 1;//又走了一步;
}
}
cout << len[k] << endl;
//查看:
for (int i = 0; i <= k; i++)
cout << i << ":" << len[i] << endl;
return 0;
}运行结果:
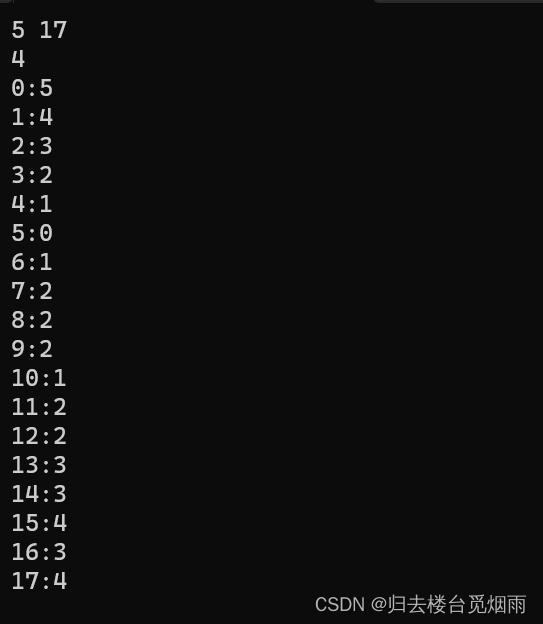
len数组中元素的实际含义:
踩到这个位置上时,这是某条路径的第len[ i ]步
为什么这样做一定是最短路径:
关键词:广度搜索、优先输出。
将最短路径的问题转化为最先输出队列的问题。