线性规划问题是运筹学最基本的问题，我们已经学过不少的解决方法，今天继续学习针对线性规划问题的另一种高效算法——网络流问题（network flow problem）

1

网络流模型

为了更好介绍该算法来龙去脉，与以往一样，从案例切入——最优炉（OOI）

最优炉股份有限公司（OOI）在位于威斯康星州和阿拉巴马州的工厂制造家用烤面包炉。制成的炉子会由火车运输到OOI位于孟菲斯和匹兹堡的两个仓库之一，而后被分销到位于弗雷斯诺、皮奥里亚和纽瓦克的顾客站点。两个仓库间也可以用公司的货车转运少量的炉子。我们的任务是做新型E27炉子下个月的分销方案。每个工厂在此期间至多可以装运1000个炉子，且目前仓库中没有存货。弗雷斯诺、皮奥里亚和纽瓦克的顾客分别需要450、500和610个炉子。仓库间的转运数量限制在25个炉子以内，但不产生费用。其他可行流的单位成本详见下表。

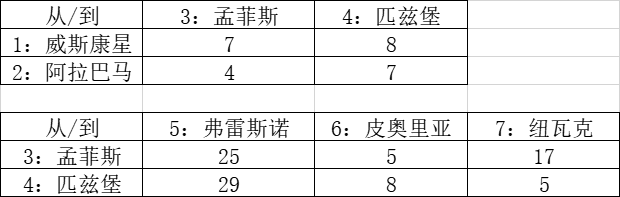
我们把OOI案例变成网络模型表示：2个工厂、2个仓库和3个顾客点组成了该有向图的7个节点。弧表示炉子的可行流，并用箭头指示方向。

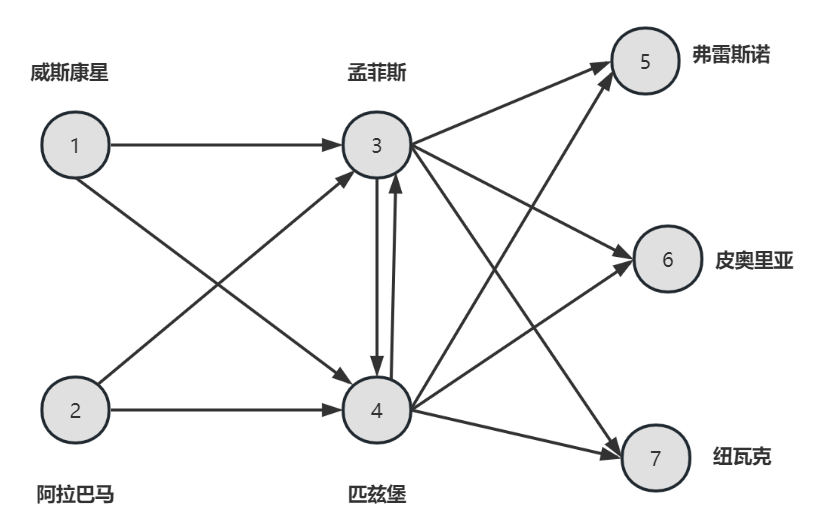
描述运筹学模型的核心是决策变量，从线性规划到网络流模型，首要找到决策变量的描述：

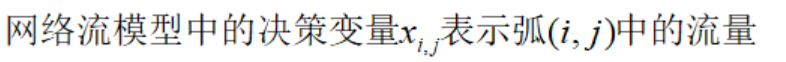
此外，我们要引入流量流动的成本以及弧上流量的上下限（即容量）：

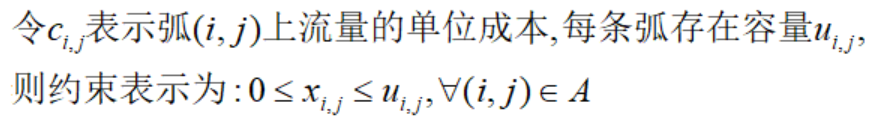
进一步，对于每个节点，我们希望：总流入-总流出=该节点指定的净需求，用符号表示：

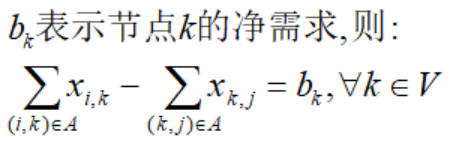
综上，我们得到最小费用网络流模型（minimum cost network flow model）：

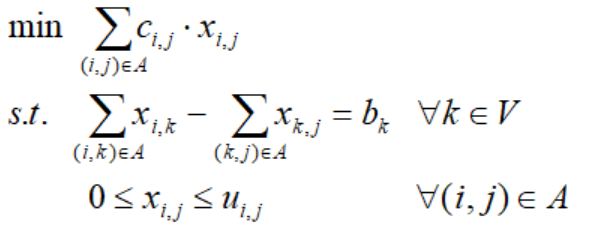
对于节点，分为三种类型。汇（sink）或需求（demand）节点是消费流，如OOI案例的顾客站点。源（source）或供给（supply）节点产生流，如OOI案例的工厂。转运（transshipment）节点仅仅传递流，如OOI案例的仓库。很显然，净需求在需求节点上为正，在供给节点上位负，在转运节点上为0

我们可以把OOI案例写成最小费用网络流模型：

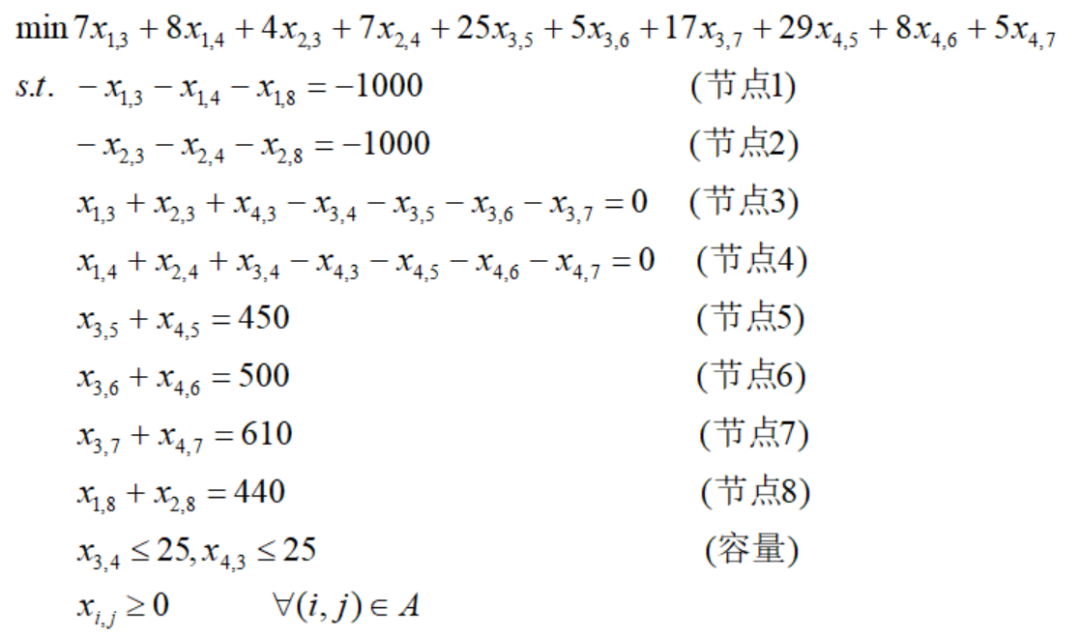
这里需要注意的是，比原来的OOI网络多了节点8。对于网络流模型，流量只在供给节点产生，而又只在需求节点消费，因此要实现流平衡必须满足：总供给=总需求。因此我们要遵循原理：

若在给定的网络流问题中，总供给小于总需求，则该问题不可行。若总供给超过总需求，则应该添加一个新的汇节点，通过从所有源节点出发的零费用弧来消费多余的供给。

OOI案例中,总供给=1000+1000>450+500+610=总需求，多余的440决定了节点8的需求。下图展示了OOI案例的一个最优解。

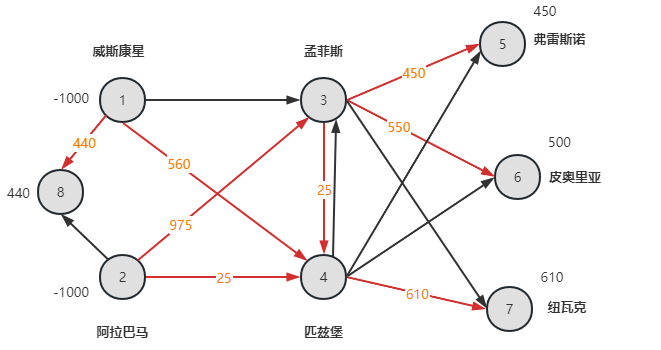
2

网络流搜索圈方向

搜索方法需要假定已有一个初始可行解进行，针对网络流问题的搜索方法更是如此。网络流情境下唯一的新要素是：创造出本身即为一个最小费用网络流问题的人工模型，使得常见算法能够适用。为此，我们只需在原始模型的所有弧上放置一个零流量的流，并添加一个人工节点。用人工弧将这一特殊节点和其他所有净需求不为零的节点连接起来，实现对供给和需求的要求。

用于计算最小费用网络流问题初始可行解的人工网络模型（artificial network model）和起始点可以通过以下方法创建：（i）为原始模型中的所有弧分配零流量的流；（ii）引入一个人工节点；（iii）创建从每个供给节点k到人工节点的人工弧，并使其流量等于给定的供给；（iv）添加从人工节点到每个需求节点k的人工弧，并使其流量等于给定的需求

比如OOI案例，我们添加人工节点0，得到人工网络模型：

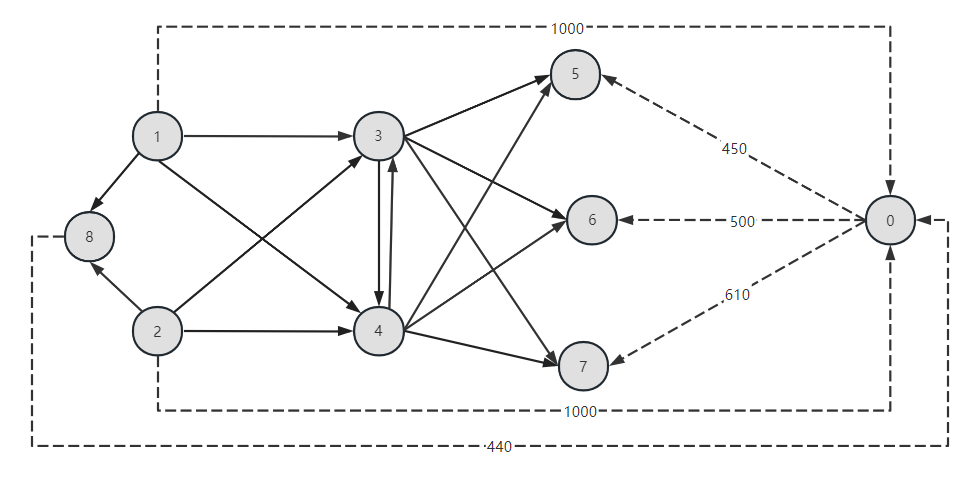
网络流模型是一种特殊的线性规划模型，因此可以写成熟悉的线性规划标准形式：

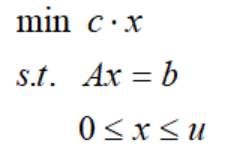
在网络流模型里，主约束矩阵A是一种特殊的结构，我们要把它与网络流的有向图联系起来。这样的矩阵被称为节点-弧关联矩阵，它们既表示流平衡要求，也表示有向图的代数描述。

节点-弧关联矩阵的每个节点对应一行、每个弧对应一列。每列中仅有两个非零项，一个为-1，位于对应弧离开节点的所在行，另一个为+1，位于弧进入节点的所在行。

仍以OOI案例举例，它们的节点-弧关联矩阵可表示为：

线性规划算法的重点在于构建可行改进方向。为了得到网络流问题的可行改进方向，我们需要了解链（chain）、圈（cycle）、路（path）的概念。路已在最短路问题给出，这里不再赘述。

链（chain）是连接两个节点的一个弧序列。在序列中，每个弧和它前一个弧恰有一个共同节点，且没有节点会被重复访问。圈（cycle）是起始和终止节点相同的一条链。

链不需要考虑弧的方向，这正是链与路的不同之处。

路是沿前进方向连接所有弧的链，回路是所有弧均沿同一方向的圈。

圈可以用前进（正方向）或后退（反方向）来连接弧。一个最小费用网络流模型的圈方向在给定有向图中某个圈的前向弧上增加流，在后向弧上减少流：

比如下面的圈1-3-6-4-1,前面两条弧都是前向的，后面两条弧都是后向的，其余的弧都不是圈的一部分。

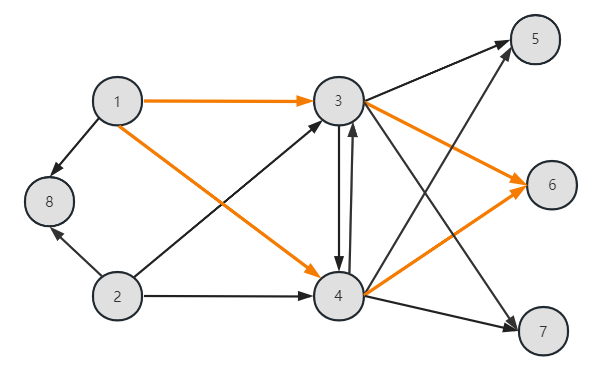
从改进搜索可行方向可知，保持可行性必须满足AΔx=0.对于节点-弧关联矩阵而言，圈方向满足“净变化为零”的条件：沿网络流模型中的某一圈方向来调整可行流，可使流平滑的约束得以满足。

举个例子证实这个原理，考虑下面有向图：

对于圈1-2-7-6-5-1，保证了节点6的流平衡。根据定义，圈方向满足：

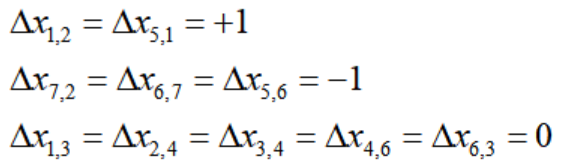
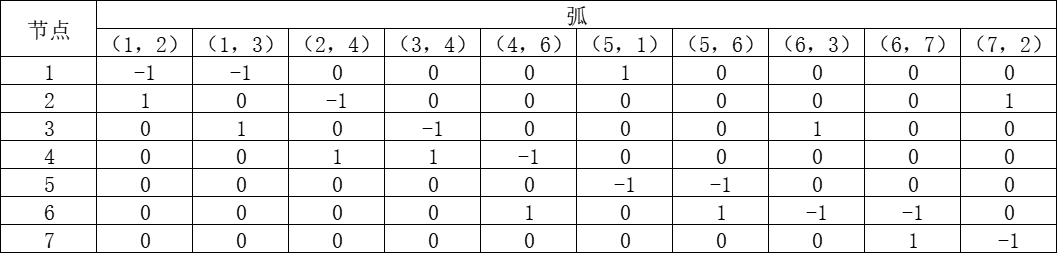
其节点-弧关联矩阵为：

对于节点6，证实原理满足净变化为零：

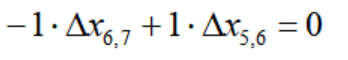
接下来，我们要找到可行改进圈方向的条件，首先是可行圈方向的充要条件：

举个例子，用（u,x)表示容量与弧的流量，对于下图，判断各个圈方向是否为一个可行圈方向。

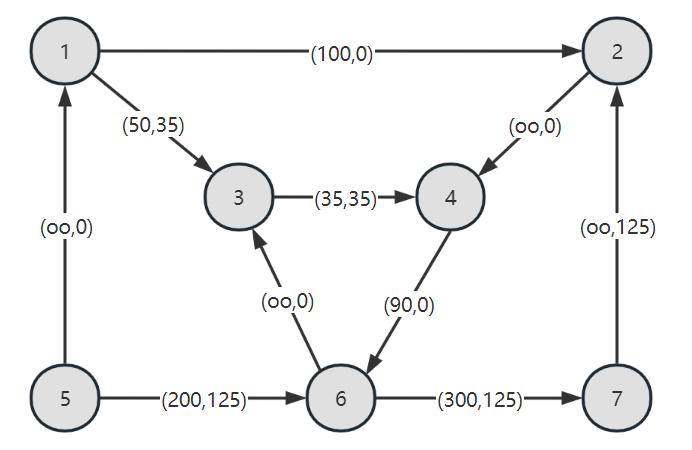
（a）1-2-7-6-5-1

该圈方向可行，因为所有后向弧的当前流量为正：（2，7），（6，7），（5，6），所有前向弧的流量未达上限：（1，2），（5，1）

（b）3-4-6-3

该圈方向不可行，因为前向弧（3，4）流量已经达到容量，不能再增加

（c）1-3-6-5-1

该圈方向不可行，因为后向弧（6，3）的流量为0，不能再减少

接下来就是改进方向的判断条件：

最后就是步长的判断：

举个例子加以说明，对于OOI案例的费用、容量和当前的流量(c,u,x)，我们在网络图标注了出来，橙色的流量表示初始流：

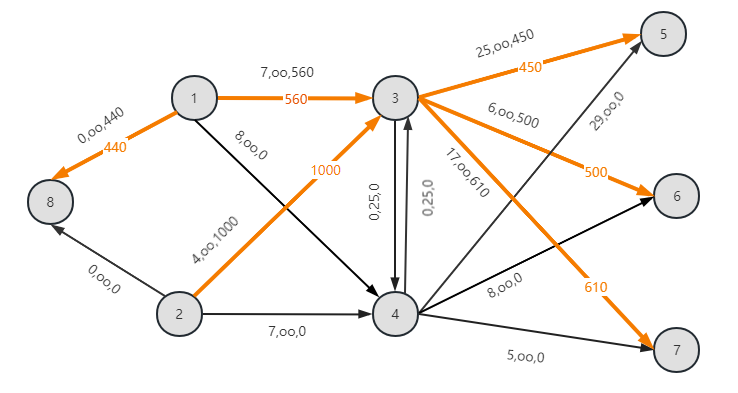
费用为：7*560+4*1000+25*450+6*500+17*610=32540

我们找到一个可行改进圈方向：2-4-7-3-2.前向弧流量均小于容量，后向弧流量均大于0，是一个可行圈。且前向弧成本与后向弧成本之差为12-21<0，是一个改进圈。

然后找最大步长：

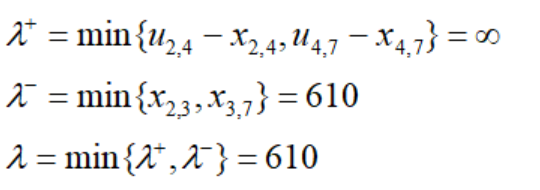
更新流：

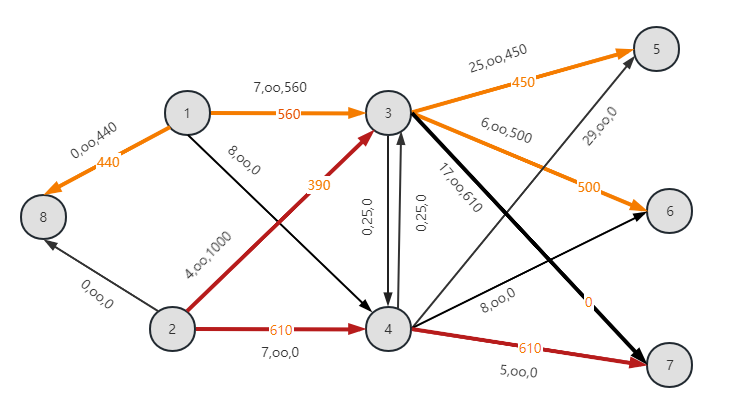
费用变为：7*560+4*390+7*610+25*450+6*500+5*610=27050

综上，我们得到退化圈方向的搜索步骤：