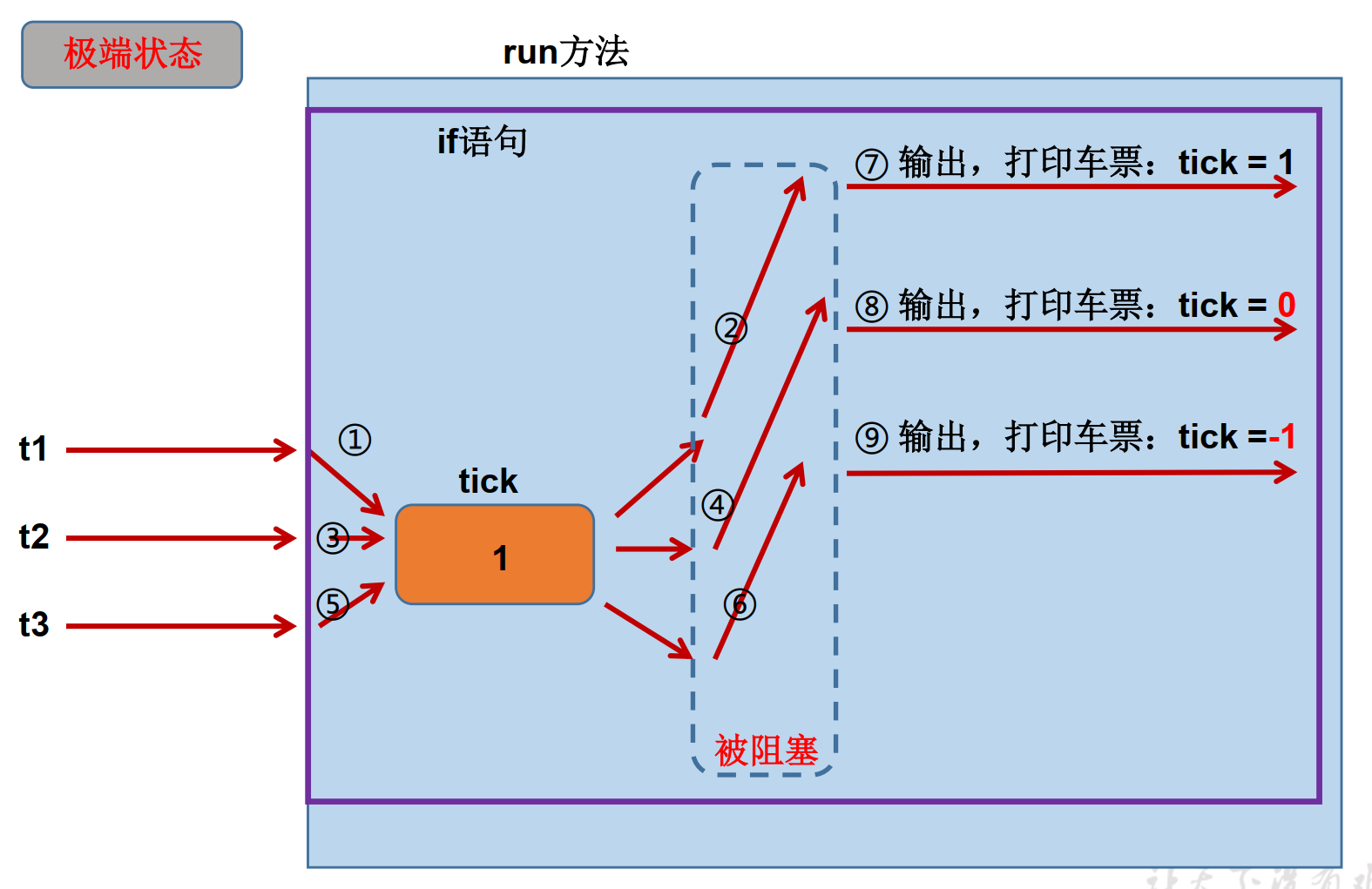
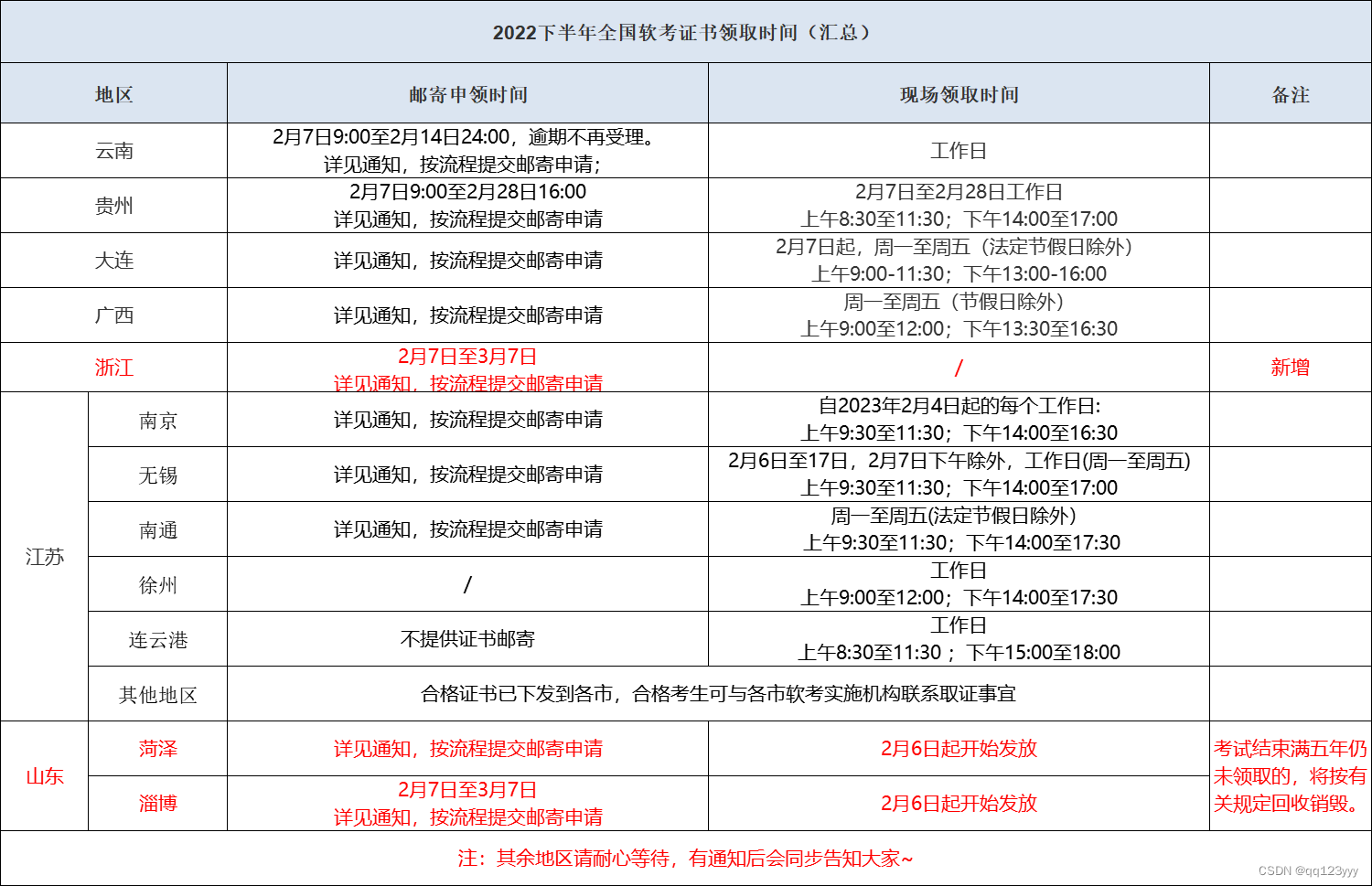
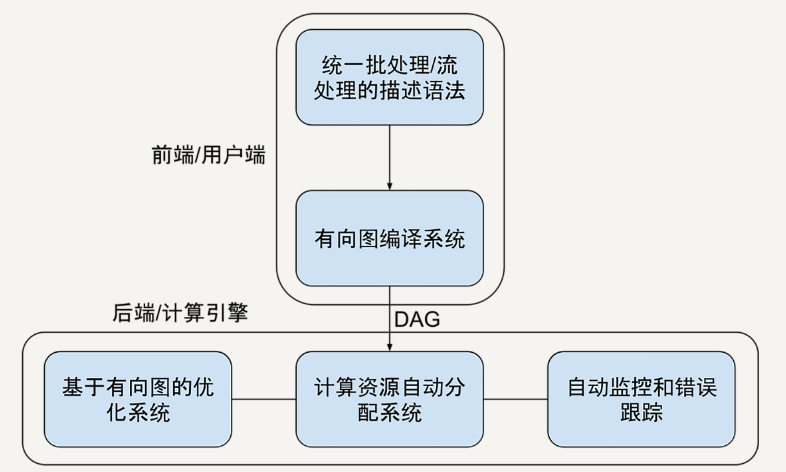
题目：

03879 * 203879 = 41566646641

这有什么神奇呢？仔细观察，203879 是个6位数，并且它的每个数位上的数字都是不同的，并且它平方后的所有数位上都不出现组成它自身的数字。

具有这样特点的6位数还有一个，请你找出它！

再归纳一下筛选要求：

1. 6位正整数

2. 每个数位上的数字不同

3. 其平方数的每个数位不含原数字的任何组成数位

分析：

仔细分析题目，我们得知两个点，

1，这个六位数的每一位数都不一样

2，这个六位数的平方的每位数字跟六位数的每位数字都不一样

那么我们就可以建一个遍历最小六位数到最大六位数的循环，建两个嵌套的if，第一个if用来判断1，第二个if用来判断2。

第一个if需要把int转数组并赋值，然后进行循环比较如果没有相等的直接进入第二个if

第二个if参考值一个是六位数，一个是六位数的平方。

六位数的平方先转为字符串，然后建一个数组并遍历赋值，六位数也是转为字符串，然后建一个数组并遍历赋值。两个数组出来了，然后两个嵌套循环进行比对

解析：

注意：因为六位数平方很大，我们需要建Bigdecimal来表示数字

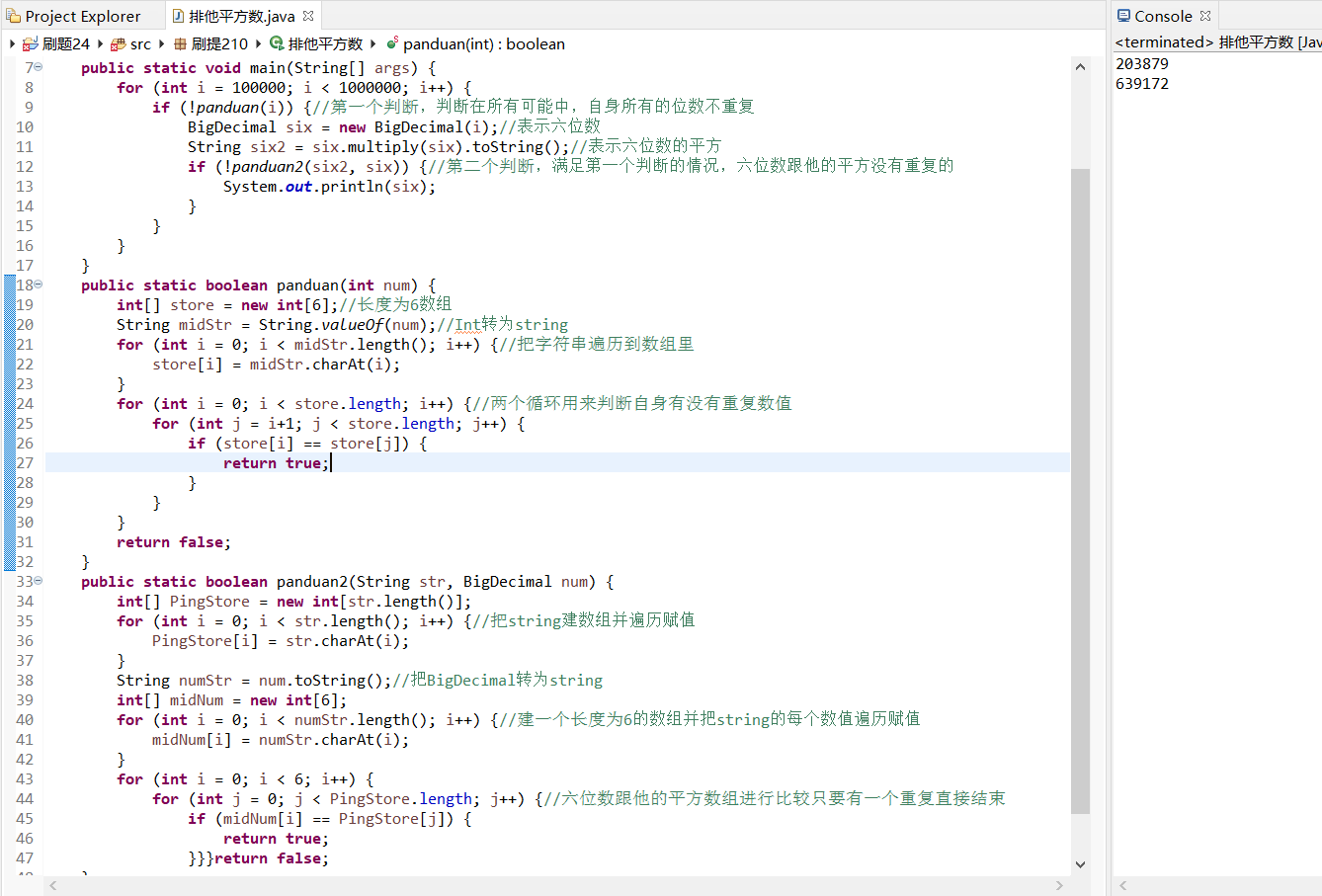
package 刷提210;

import java.math.BigDecimal;

public class 排他平方数 {

    public static void main(String[] args) {
        for (int i = 100000; i < 1000000; i++) {
            if (!panduan(i)) {//第一个判断，判断在所有可能中，自身所有的位数不重复
                BigDecimal six = new BigDecimal(i);//表示六位数
                String six2 = six.multiply(six).toString();//表示六位数的平方
                if (!panduan2(six2, six)) {//第二个判断，满足第一个判断的情况，六位数跟他的平方没有重复的
                    System.out.println(six);
                }
            }
        }
    }
    public static boolean panduan(int num) {
        int[] store = new int[6];//长度为6数组
        String midStr = String.valueOf(num);//Int转为string
        for (int i = 0; i < midStr.length(); i++) {//把字符串遍历到数组里
            store[i] = midStr.charAt(i);
        }
        for (int i = 0; i < store.length; i++) {//两个循环用来判断自身有没有重复数值
            for (int j = i+1; j < store.length; j++) {
                if (store[i] == store[j]) {
                    return true;
                }
            }
        }
        return false;
    }
    public static boolean panduan2(String str, BigDecimal num) {
        int[] PingStore = new int[str.length()];
        for (int i = 0; i < str.length(); i++) {//把string建数组并遍历赋值
            PingStore[i] = str.charAt(i);
        }
        String numStr = num.toString();//把BigDecimal转为string
        int[] midNum = new int[6];
        for (int i = 0; i < numStr.length(); i++) {//建一个长度为6的数组并把string的每个数值遍历赋值
            midNum[i] = numStr.charAt(i);
        }
        for (int i = 0; i < 6; i++) {
            for (int j = 0; j < PingStore.length; j++) {//六位数跟他的平方数组进行比较只要有一个重复直接结束
                if (midNum[i] == PingStore[j]) {
                    return true;
                }}}return false;
    }

}