二叉平衡搜索树
- 一、平衡二叉搜索树的概述
- 1. 平衡二叉树的性质
- 2. 平衡二叉树的最小节点数(公式及其原理)
- a. 树高度和深度的区别
- b. 原理
- 二、平衡二叉树的创建和调整
- 1. 节点
- 2. 旋转
- 四种姿态
- a. LL旋转
- b. RR旋转
- c. LR旋转
- d. RL旋转
- 2. 节点的插入
- 3. 节点的删除
- 4. 中序遍历
一、平衡二叉搜索树的概述
平衡二叉树总称应该为平衡二叉查找树,也可称AVL树(满足平衡条件的二叉查找树),也就是说平衡二叉查找树的前提是二叉搜索树(二叉搜索树汇总)。
二叉搜索树进行插入、删除、查找操作时,时间复杂度是 O(logn),但当这棵二叉搜索树为斜树时,那么时间复杂度会引来最坏的结果 O(n)。
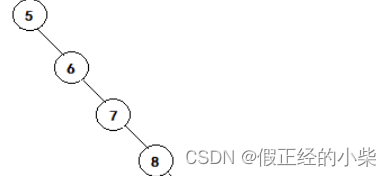
当尽可能的将树俩边保持平衡时,这时复杂度会引来最好的结果。
1. 平衡二叉树的性质
平衡二叉树(Balanced Binary Tree)具有以下性质:
- 要么是空树要么左右两个子树的高度差的绝对值不超过1;
- 左右子树也都是一棵平衡二叉树;
- 每个节点都有一个平衡因子(Balanced Factor),任意一个节点的平衡因子的值为 -1、0、1,计算公式是 左子树高度 - 右子树高度。
2. 平衡二叉树的最小节点数(公式及其原理)
设 Nh 是高度为 h 的平衡二叉树的最小结点数:
==》Nh = Nh-1 + Nh-2 + 1
学的时候会发现总把它和斐波那契数列放在一起去进行理解。斐波那契数列又可以用分治和递归的思想去解决,而最小节点数用分治思想是不好理解的,递归反而容易理解些,可以理解为由上至下。
a. 树高度和深度的区别
理解最小节点数怎么来的之前得先理解树高度和深度的区别:
定义:
高度:结点到叶子节点最长简单路径的条数;
深度:根节点到该节点的最长简单路径边的条数。
注意:这里的条数规定是 根结点的深度和 叶子结点的高度 是为 0。
区别:
深度是从顶到该节点,高度是从低到该节点。
b. 原理
根据平衡二叉树的定义可知:左右子结点高度差的绝对值<=1,那么对于高度为 h 的平衡二叉树无非就三种情况:
- 左结点 h-1 的高度,右结点 h-2 的高度
- 右结点 h-1 的高度,左结点 h-2 的高度
- 左右结点都为 h-1 的高度。
对于左右子节点来说无非就是新的根节点、新的平衡二叉树,想得到最小节点数,那肯定左右子结点新构成的平衡二叉树的结点也应该满足最小的节点数,且情况为 一个子树为 h-1 的高度, 一个子树为 h-2 的高度。
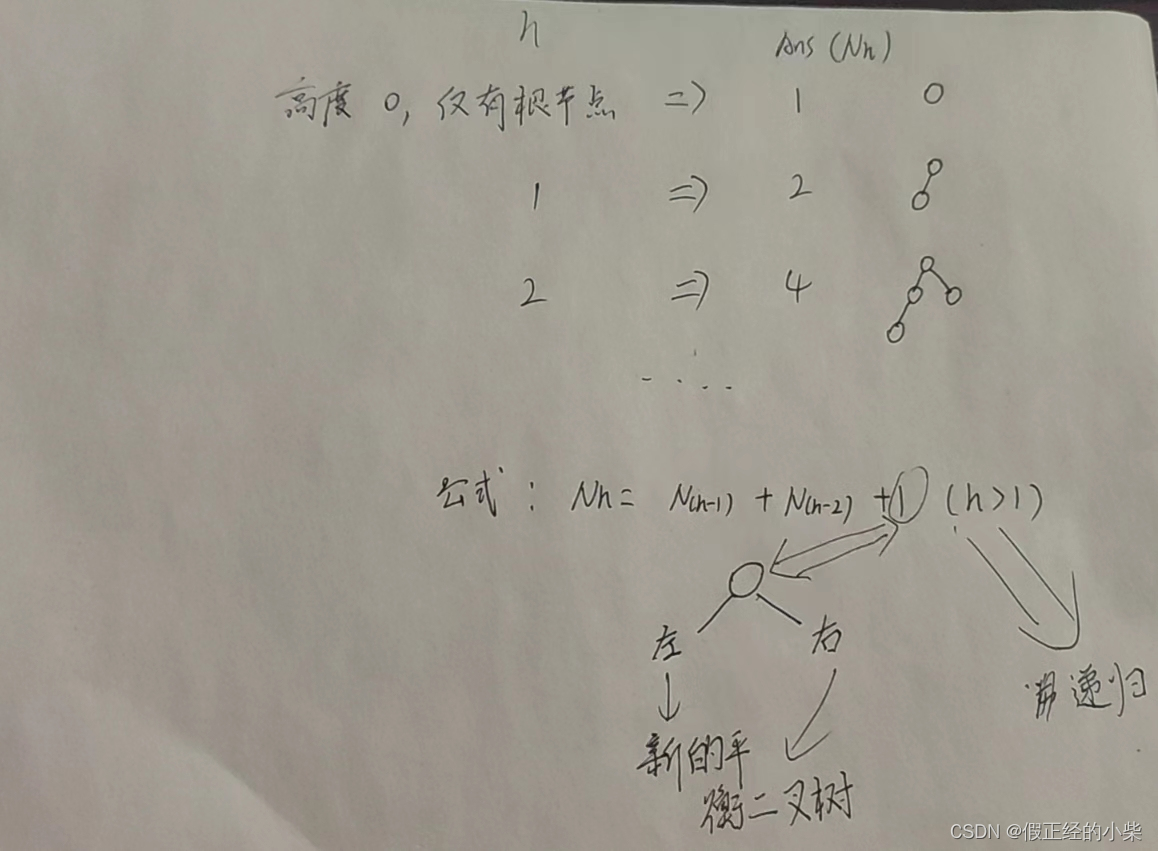
注意:这里的高度是以平衡二叉树的根节点为目标结点,Ans(Nh)表示最后结果也就是最小节点数。
(递归 + 公式 更容易理解些,看得懂就行)
二、平衡二叉树的创建和调整
1. 节点
建立一个
AVLTree类,表示平衡二叉搜索树类,由于该二叉树是由节点组成的,那在该类内部有个节点内部类AVLTreeNode类,该二叉树也是二叉搜索树,由于需要对节点值进行比较,所以也运用了泛型,节点对象只用实现了Comparable接口的类对象。
public class AVLTree<T extends Comparable<T>> {
private AVLTreeNode<T> mRoot;
class AVLTreeNode<T extends Comparable<T>>{
public int height;
public AVLTreeNode<T> left;
public AVLTreeNode<T> right;
T val;
public AVLTreeNode() {}
public AVLTreeNode(AVLTreeNode<T> left, AVLTreeNode<T> right, T val) {
this.left = left;
this.right = right;
this.val = val;
}
}
}
2. 旋转
四种姿态
当对 AVL 树进行插入、删除操作时,可能会使得 AVL 树失去平衡。这种失去平衡概括为四种姿态:
LL(左左)、LR(左右)、RR(右右)、RL(右左)。

-
LL:Left Left,也称为“左左”。插入或删除一个节点后,根节点的左子树的左子树还有非空子节点,导致“根的左子树的高度”比”根的右子树的高度“大 2,平衡因子 > 1,导致AVL 树失去平衡。 -
LR:Left Right,也称为”左右“。插入或删除一个节点后,根节点的左子树的右子树还有非空子节点,导致”根的左子树的高度“比”根的右子树的高度“大2,平衡因子 > 1,导致AVL 树失去了平衡。 -
RL:Right Left,也称为”右左“。插入或删除一个节点后,根节点的右子树的左子树还有非空子节点,导致”根的右子树的高度“比”根的左子树的高度“大2,平衡因子 < -1,导致AVL 树失去了平衡。
-
RR:Right Right,也称为”右右“。插入或删除一个节点后,根节点的右子树的右子树还有非空子节点,导致”根的右子树高度“比”根的左子树高度“大2,平衡因子 < -1,导致AVL 树失去了平衡。
(上图分别对四种姿态进行了图形展示)
当 AVL 失去平衡之后,可以通过旋转使其恢复平衡。
a. LL旋转
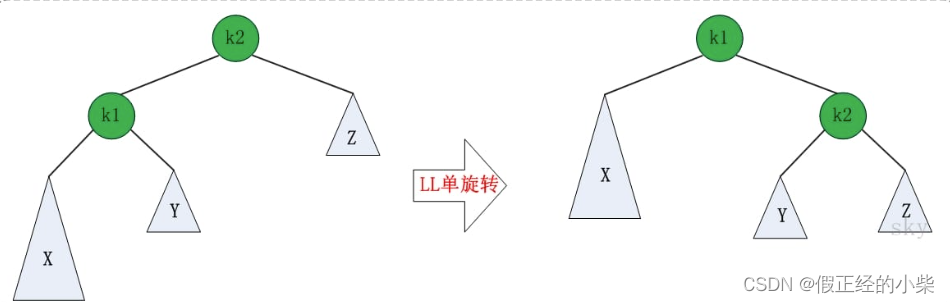
左边是失去平衡的二叉树,右边是恢复后的 AVL 树。k2 是最小不平衡子树根节点,旋转过程中他扮演着主角。
LL 使得AVL 树失去平衡的 AVL 树,是向右旋转,向右旋转 k1 会去替代k2 的位置,k2会成为k1的右孩子,k1 的右孩子会成为新k2 的左孩子。这样做不仅可以 平衡二叉树的性质再次得到满足。
/**
* LL 旋转
* @param k2 要旋转的最小不平衡子树的根节点
* @return 返回替代k2的节点,也可以说返回该最小不平衡子树的根节点。
*/
private AVLTreeNode<T> LLRotation(AVLTreeNode<T> k2){
AVLTreeNode<T> k1 = k2.left;// 标记节点,用来暂时指向k2 的左孩子
// 要开始旋转了哦
k2.left = k1.right;
k1.right = k2;
k2.height = Math.max(height(k2.left),height(k2.right)) + 1;
k1.height = Math.max(height(k1.left),height(k1.right)) + 1;
return k1;
}
注意:该方法重新返回(最小不平衡树)根节点是有用的,插入,以及LR和RL旋转都是有用的。
b. RR旋转
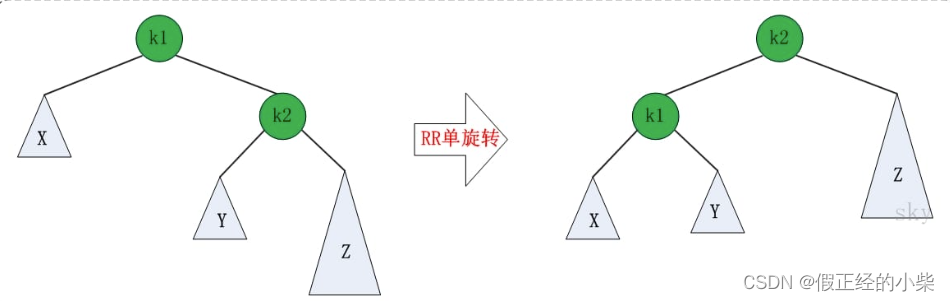
注意:和上面的LL是相反的。代码里面的k2指的是图里的k1,k1指的是图里的k2。
/**
* @param k2
* @return 返回最小不平衡子树的根节点
*/
private AVLTreeNode<T> RRRotation(AVLTreeNode<T> k2) {
AVLTreeNode<T> k1 = k2.right;
k2.right = k1.left;
k1.left = k2;
k2.height = Math.max(height(k2.left),height(k2.right)) + 1;
k1.height = Math.max(height(k1.left),height(k1.right)) + 1;
return k1;
}
c. LR旋转
- 从右往左看,先RR转,在LL转。

- 第一次旋转是围绕"k1"进行的"RR旋转",第二次是围绕"k3"进行的"LL旋转"。
代码就很简单啦:
/**
* @param root
* @return 返回最小不平衡子树的根节点
*/
private AVLTreeNode<T> LRRotation(AVLTreeNode<T> root) {
root.left = RRRotation(root.left);
return LLRotation(root);
}
d. RL旋转
- 先 LL 转,再 RR 转咯。

- 第一次旋转是围绕"k3"进行的"LL旋转",第二次是围绕"k1"进行的"RR旋转"。
/**
* @param root
* @return 返回最小不平衡子树的根节点
*/
private AVLTreeNode<T> RLRotation(AVLTreeNode<T> root) {
root.right = LLRotation(root.right);
return RRRotation(root);
}
2. 节点的插入
本应该插入应该在前的,因为它可以更好的测试数据。
但是插入又离不开旋转,所以还是得先解释旋转。
结点的插入呢?和二叉搜索树差不多。多了个AVL树是否还平衡的判断和结点高度的更新。
直接上代码,更清楚:
// 供用户使用的方法
public void insert(T key){
if(key!=null){
mRoot = insert(mRoot,key);
}
}
// 插入细节
private AVLTreeNode<T> insert(AVLTreeNode<T> root,T key){
if(root==null){
root = new AVLTreeNode<T>(null,null,key);
}else{
int cmp = key.compareTo(root.val);
if(cmp<0){
root.left = insert(root.left, key);
// 插入节点如果AVL 树失去平衡,则进行相应的调节
if(height(root.left) - height(root.right) == 2){
// 这节点是插入在左孩子的,要么就是LL 要么就是LR
// LL
if(key.compareTo(root.left.val)<0){
root = LLRotation(root);
}else{
root = LRRotation(root);
}
}
}else if(cmp>0){
root.right = insert(root.right,key);
// 和上面一样,判断是否失去平衡然后做调节
if(height(root.right) - height(root.left) == 2){
if(key.compareTo(root.right.val)>0) {
root = RRRotation(root);
}else{
root = RLRotation(root);
}
}
}else{
// 这里咱自定义一个异常类 ValOfAVLNodeEqual
try {
throw new ValOfAVLNodeEqual("AVL 树中不支持节点的数据相等");
} catch (ValOfAVLNodeEqual e) {
e.getMessage();
}
}
}
// 递归回溯的途中需要更新节点的高度
root.height = Math.max(height(root.left),height(root.right)) + 1;
// 完美返回
return root;
}
3. 节点的删除
删除和BST 一样分三种情况:
- 左右孩子都存在;
- 单个孩子存在;
- 无孩子。
什么查找代码,寻找左子树最大值节点。。。很多重复代码,不想写了。
可以看看这个的删除操作:
平衡二叉树删除操作
4. 中序遍历
有了上面的噔噔噔一些操作后,来个遍历收尾。
返回一个LIst 集合,可以操作可以输出。完美~
private List<T> valList = new ArrayList<>();
/**
* 咱来个中序遍历,有序
*/
public List<T> orderTraversal(){
valList.clear();
orderTraversal(mRoot);
return valList;
}
public void orderTraversal(AVLTreeNode<T> node){
if(node!=null){
orderTraversal(node.left);
valList.add(node.val);
orderTraversal(node.right);
}
}
![[转]深度学习 Transformer架构解析](https://img-blog.csdnimg.cn/img_convert/ca36d743d00a5e8479c5475ca412cb0a.png)