gitee链接 :基于时间序列的 基-2 FFT算法程序
我的 gitee 程序目前没有公开,目前仅是给自己的程序做一个备份的目的。
但是大家可以使用我博客贴出来的程序,二者是一样的。
文章目录
- 1.程序使用方法
- 2.代码
- 3.验证
1.程序使用方法
1.先补零至2的整数幂次,调用 AddZero
2.再进行码位倒序,调用 Reverse
3.最后进行 fft,调用 fft
本人先是浏览了其他人在网上的实现,没有搞懂。
于是,在自己独立完成 补零AddZero函数,以及 码位倒序 Reverse函数之后,使用了大量的时间,将DFT公式进行分解了如下的分解和验证:
首先,将 N点的DFT 的公式 分解为 2个 N/2点的DFT之和,并画了蝶形图,以及使用 4个真实的数字验证正确。
然后,将 2个 N/2点的DFT之和 分解为 4个 N/4点的DFT之和,并画了蝶形图,以及使用 8个真实的数字验证正确。
最后,将 4个 N/4 点的DFT之和 分解为 8 个 N/8点的DFT之和,并画了蝶形图,以及使用 16个真实的数字验证正确。
通过研究 3 幅鲽形图,找出其中的规律,完成了 fft 函数,并使用很多组数字进行验证,与 matlab 的结果,以及自己手算的结果均一致。
2.代码
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
#define PI 3.141592654
typedef struct
{
float real;
float img;
}complex;
/*复数加法*/
complex add(complex a, complex b)
{
complex c;
c.real = a.real + b.real;
c.img = a.img + b.img;
return c;
}
/*复数减法*/
complex sub(complex a, complex b)
{
complex c;
c.real = a.real - b.real;
c.img = a.img - b.img;
return c;
}
/*复数乘法*/
complex mul(complex a, complex b)
{
complex c;
c.real = a.real * b.real - a.img * b.img;
c.img = a.real * b.img + a.img * b.real;
return c;
}
// 码位倒序
void Reverse(int* arr, int n)
{
if (arr == NULL || n <= 1)
return;
// 计算 n-1 的二进制位数
int bitsCount = 0;//二进制位数计数器
for (int i = 0; i < 32; i++)
{
if ((((n - 1) >> i) & 1) == 1)
bitsCount = i + 1;
}
// 重排序后的下标
int* reorderIndex = (int*)malloc(n * 4);
// 重排序后的序列
int* reorderIndexArray = (int*)malloc(n * 4);
// 计算原下标的倒序,存入 reorderIndex
for (int i = 0; i < n; i++)
{
int index = i;
int newIndex = 0;
for (int j = 0; j < bitsCount; j++)
{
// 如果下标的这一位为1,则构造一个 第(bitsCount - j)位为 1 的数字,或到 newIndex,达到 newIndex 的倒数第 j 位为1的目的
if (((index >> j) & 1) == 1)
{
int tmp = (1 << (bitsCount - 1 - j));
newIndex |= tmp;
}
else// 如果下标的这一位为0,则不用管
{
}
}
reorderIndex[i] = newIndex;
}
/*printf("\n 重排序后的下标:");
for (int i = 0; i < n; i++)
{
printf("%d ,", reorderIndex[i]);
}*/
/*printf("\n 重排序后的序列:");*/
// 重排序后的序列
for (int i = 0; i < n; i++)
{
reorderIndexArray[i] = arr[reorderIndex[i]];
//printf("%d ,", reorderIndexArray[i]);
}
// 把重排序后的序列覆盖到原数组
for (int i = 0; i < n; i++)
{
arr[i] = reorderIndexArray[i];
}
free(reorderIndex);
reorderIndex = NULL;
free(reorderIndex);
reorderIndexArray = NULL;
}
int newLength = 0;//新数组的长度
//为原数组补零
int* AddZero(int* arr, int n)
{
if (n <= 0 || arr == NULL)
{
return NULL;
}
int* newArr = NULL;
if (n == 1)
{
newArr = (int*)malloc(2 * 4);
newArr[0] = arr[0];
newArr[1] = 0;
newLength = 2;
return newArr;
}
// 计算 n-1 的二进制位数
int bitsCount = 0;//二进制位数计数器
for (int i = 1; i < 32; i++)
{
//判断第 i 位是否是1,如果是1,则最高位起码有 i+1 位
if ((((n - 1) >> i) & 1) == 1)
bitsCount = i + 1;
}
// 知道了有多少个二进制位后,再判断第1位到最高位之间是否有1
// 如果第 1 到 bitsCount-1 位有1,说明不是 2 的整数幂
int num = n;
int mi = 0;// 存储2的幂次
for (int i = 0; i < bitsCount - 1; i++)
{
if (((num >> i) & 1) == 1)
{
// 说明不是 2 的整数幂
// 将 num 的最高位往前进一位,然后后面的 1 全部置为0,以此得到比它大的最近的2的整数幂
num = num & (1 << bitsCount);
mi = bitsCount;
break;
}
}
// mi != 0说明原数组长度不为 2 的整数幂次,因此需要补零
if (mi != 0)
{
// 补零后的数组长度
newLength = pow(2, mi);//补零到 2 的 mi次
newArr = (int*)malloc(newLength * 4);
for (int i = 0; i < n; i++)
{
newArr[i] = arr[i];
}
// 补零后的数组的长度与原数组的长度之差
int diff = newLength - n;
// 在数组元素末尾补零
for (int i = 0; i < diff; i++)
{
newArr[n + i] = 0;
}
}
return newArr;
}
complex** fft(int* arr, int n)
{
if (n <= 0 || arr == NULL)
return NULL;
// 先计算数组长度为 2 的多少次幂,这个幂次代表有FFT的蝶形运算有多少级
// 因为在调用这个函数之前,要调用 Reverse 和 AddZero 这两个函数,已经保证了 n 为 2 的整数次幂
// 2的整数次幂的数字,除了最高位为1,其余位都为0,且最高位是第几位,它就是2的多少次幂
// 所以我们要知道n的二进制中1的位置
int mi = 0;// 2 的 mi 次等于n
for (int i = 0; i < 32; i++)
{
if (((n >> i) & 1) == 1)
{
mi = i;
break;
}
}
if ((pow(2, mi) != n) || (mi == 0))
{
printf("n=%d 不是2的整数次幂,无法进行FFT!!!\n", n);
return NULL;
}
// 开辟一个存放 频谱 的数组
complex** a = (complex**)malloc(n * sizeof(complex*));
// 将数组的元素拷贝进去,数组 a 就是存放蝶形运算的输入的元素,运算的结果也会覆盖数组 a
for (int i = 0; i < n; i++)
{
a[i] = (complex*)malloc(sizeof(complex));
a[i]->real = (float)arr[i];
a[i]->img = 0;
}
// level 代表一共有多少级
// 第一步:先移动到第 level 级
for (int level = 0; level < mi; level++)
{
// 这一级中包含的大蝶的数量, 使用的公式为 n / pow(2, level+1),下面代码优化为了移位运算
int bigButterFlyCount = n >> (level + 1);
// 每个大蝶中包含的小蝶的数量
int smallButterFlyCount = pow(2, level);
// 计算每个大蝶中包含的小蝶的数量的另一个简单的方法如下面这行代码:
// int smallButterFlyCount = (n / bigButterFlyCount) >> 1;
// 每个小蝶两个输入元素下标的距离
int smallButterFly_Input_Index_Distance = pow(2, level);
// 第二步:移动到第 level 级的第 i 个大蝶
for (int i = 0; i < bigButterFlyCount; i++)
{
// 这个大碟的第一个输入元素的下标
int bigButterFly_Input_First_Index = smallButterFlyCount * i * 2;
// 第三步:移动到第 level 级的第 i 个大蝶中的第 j 个小蝶
for (int j = 0; j < smallButterFlyCount; j++)
{
// 这个大碟中的第 j 个小蝶的第一个输入元素的下标
int smallButterFly_Input_First_Index = bigButterFly_Input_First_Index + j;
// 这个大碟中的第 j 个小蝶的第二个输入元素的下标
int smallButterFly_Input_Second_Index = smallButterFly_Input_First_Index + pow(2, level);
// 第 j 个小蝶的第一个输入元素
complex* start_input = a[smallButterFly_Input_First_Index];
// 第 j 个小蝶的第二个输入元素
complex* end_input = a[smallButterFly_Input_Second_Index];
// 计算第 j 个小蝶的旋转因子
complex w;
w.real = cos(2*PI / n * j * (pow(2, mi - level - 1)));
w.img = -sin(2 * PI / n * j * (pow(2, mi - level - 1)));
// 进行蝶形运算,上加下减
complex first = add(*first_input, mul(*second_input, w));
complex second = sub(*first_input, mul(*second_input, w));
// 将蝶形运算的输出覆盖回原来位置的元素上
first_input->real = first.real;
first_input->img = first.img;
second_input->real = second.real;
second_input->img = second.img;
}
}
}
return a;
}
void main()
{
int arr[] = {1,357,7,8,2,3,4,5};
// 对原数组进行补零
int* newArr = AddZero(arr, sizeof(arr) / sizeof(int));
if (newArr == NULL)
{
// 说明原数组长度为 2 的整数幂次,不需要补零
printf("不需要补零\n");
int length = sizeof(arr) / sizeof(int);
printf("数组如下:\n");
for (int i = 0; i < length; i++)
{
printf("%d ", arr[i]);
}
// 码位倒序
Reverse(arr, length);
printf("\n码位倒序后的数组如下\n");
for (int i = 0; i < length; i++)
{
printf("%d ", arr[i]);
}
// 进行 fft 蝶形运算
complex** c = fft(arr, length);
printf("\nfft 的结果如下:\n");
for (int i = 0; i < length; i++)
{
printf("%f, %fi\n", c[i]->real, c[i]->img);
}
for (int i = 0; i < length; i++)
{
free(c[i]);
c[i] = NULL;
}
free(c);
c = NULL;
}
else
{
printf("补零后的新数组如下:\n");
for (int i = 0; i < newLength; i++)
{
printf("%d ", newArr[i]);
}
// 码位倒序
Reverse(newArr, newLength);
printf("\n码位倒序后的数组如下:\n");
for (int i = 0; i < newLength; i++)
{
printf("%d ", newArr[i]);
}
// 进行 fft 蝶形运算
complex** c = fft(newArr, newLength);
printf("\nfft 的结果如下:\n");
for (int i = 0; i < newLength; i++)
{
printf("%f, %fi\n", c[i]->real, c[i]->img);
}
free(newArr);
newArr = NULL;
for (int i = 0; i < newLength; i++)
{
free(c[i]);
c[i] = NULL;
}
free(c);
c = NULL;
}
}
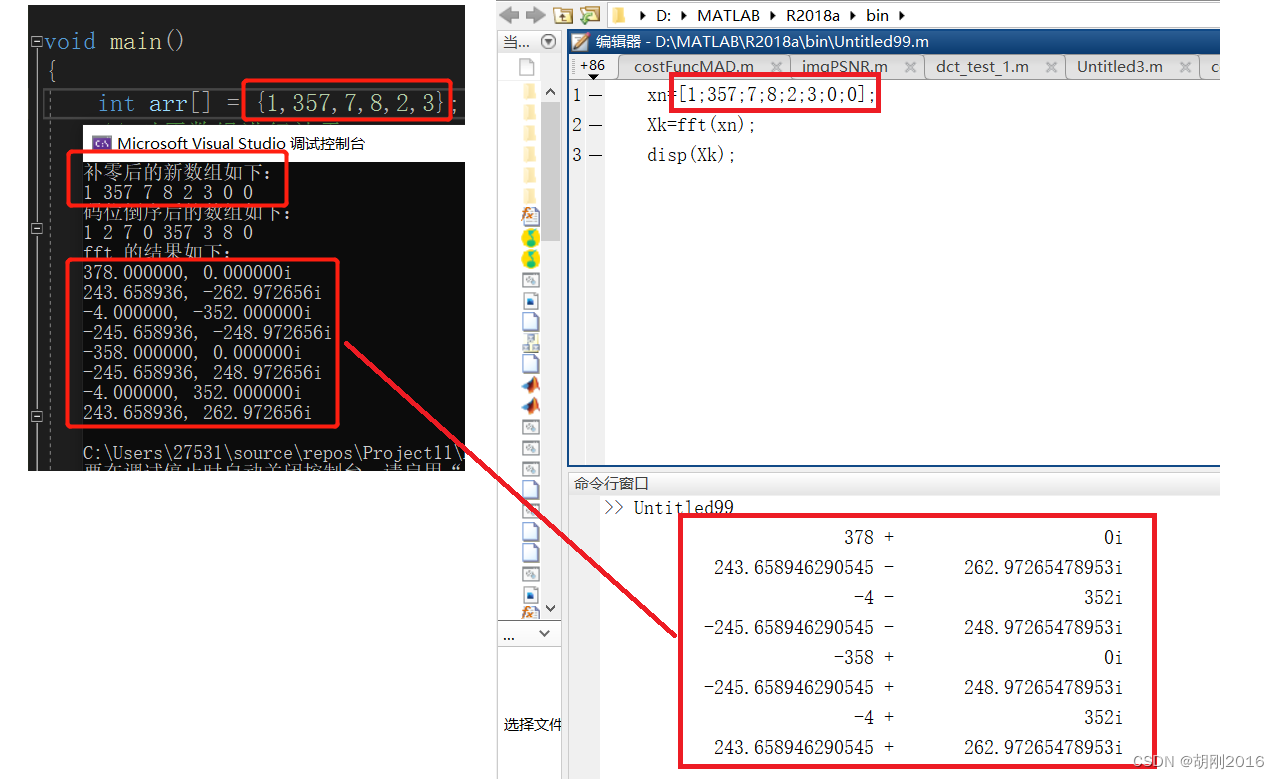
3.验证
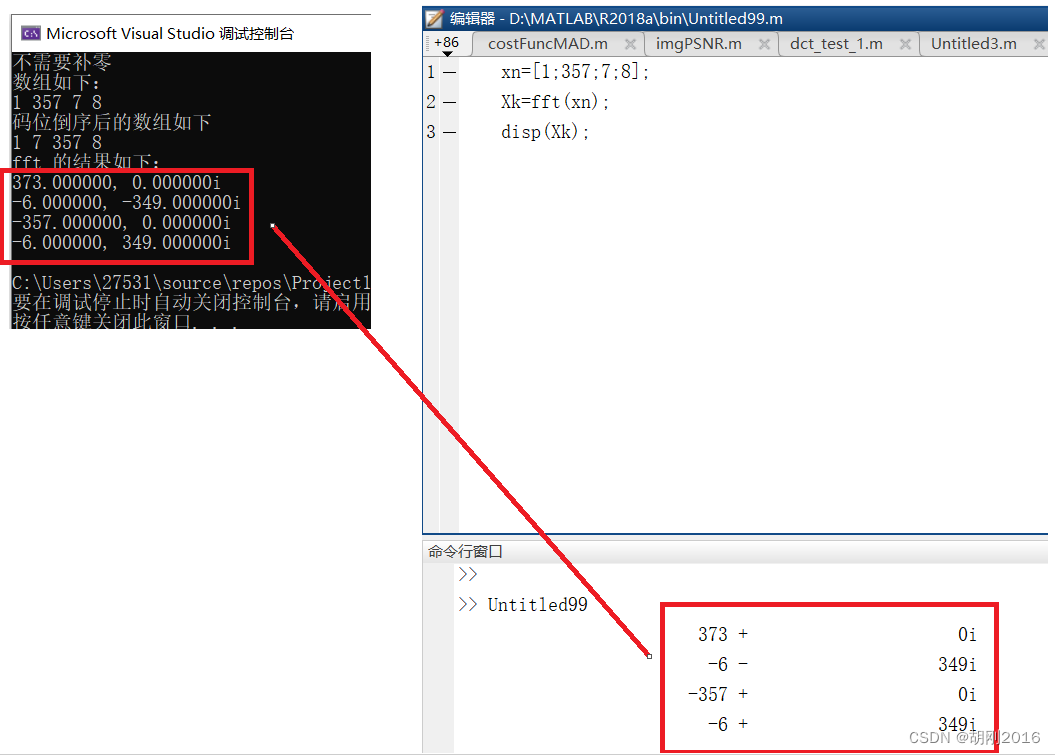
可以对比 matlab 程序和例子进行验证
xn=[1;357;7;8];
Xk=fft(xn);
disp(Xk);
结果对比
xn=[1;357;7;8;2;3;0;0];
Xk=fft(xn);
disp(Xk);