牛客 面试必刷TOP101 题解（3、二叉树）

news2025/11/1 6:42:01

23 二叉树的前序遍历

在这里插入图片描述

/**
 * struct TreeNode {
 *	int val;
 *	struct TreeNode *left;
 *	struct TreeNode *right;
 *	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
#include <vector>
class Solution {
public:
    vector<int> ans;
    void show(TreeNode* r){
        if(!r) return;
        ans.push_back(r->val);
        show(r->left);
        show(r->right);
    }
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param root TreeNode类 
     * @return int整型vector
     */
    vector<int> preorderTraversal(TreeNode* root) {
        // write code here
        show(root);
        return ans;
    }
};

24 二叉树的中序遍历

在这里插入图片描述

/**
 * struct TreeNode {
 *  int val;
 *  struct TreeNode *left;
 *  struct TreeNode *right;
 *  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
class Solution {
  public:
    vector<int> ans;
    void show(TreeNode* r) {
        if (!r) return;

        show(r->left);
        ans.push_back(r->val);
        show(r->right);
    }
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @return int整型vector
     */
    vector<int> inorderTraversal(TreeNode* root) {
        // write code here
        show(root);
        return ans;
    }
};

25 二叉树的后序遍历

在这里插入图片描述

/**
 * struct TreeNode {
 *  int val;
 *  struct TreeNode *left;
 *  struct TreeNode *right;
 *  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
class Solution {
  public:
    vector<int> ans;
    void show(TreeNode* r) {
        if (!r) return;

        show(r->left);

        show(r->right);
        ans.push_back(r->val);
    }
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @return int整型vector
     */
    vector<int> postorderTraversal(TreeNode* root) {
        // write code here
        show(root);
        return ans;
    }
};

26 求二叉树的层序遍历

在这里插入图片描述

/**
 * struct TreeNode {
 *	int val;
 *	struct TreeNode *left;
 *	struct TreeNode *right;
 * };
 */

#include <cstddef>
#include <queue>
#include <vector>
class Solution {
public:
    /**
     * 
     * @param root TreeNode类 
     * @return int整型vector<vector<>>
     */
    vector<vector<int> > levelOrder(TreeNode* root) {
        // write code here
      
        vector<vector<int> > ans;
        vector<int> Temp;
        queue<TreeNode* > Q;


        if(!root) return ans;
        Q.push(root);
        Temp.push_back(root->val);
        ans.push_back(Temp);

        // cout << Q.size() << endl;
        while (Q.size()) {
            // cout << Q.size() << endl;
            queue<TreeNode* > TQ;
            Temp.clear();
            int m = ans.size(); 
            while (Q.size()) {
                TreeNode* cur = Q.front();Q.pop();
                if(cur->left){
                    Temp.push_back(cur->left->val);
                    TQ.push(cur->left);
                }
                if(cur->right){
                    Temp.push_back(cur->right->val);
                    TQ.push(cur->right);
                }
            }
            if(Temp.size())
                ans.push_back(Temp);
            Q = TQ;
        }
        
        return ans;
        
    }
};

27 按之字形顺序打印二叉树

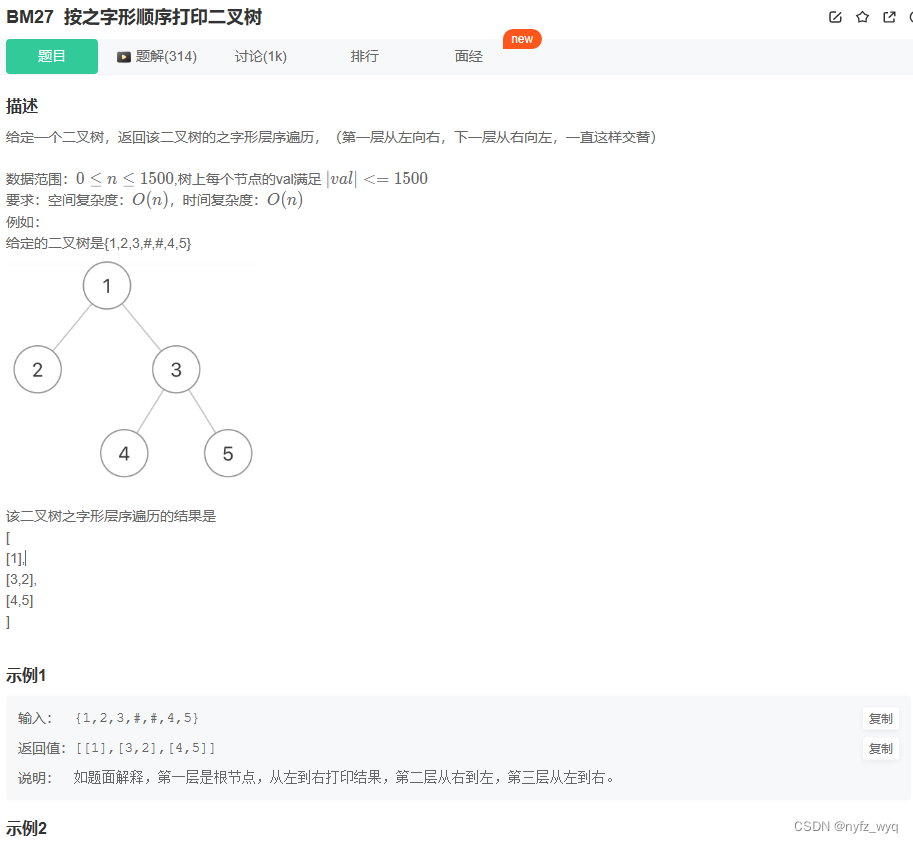
在这里插入图片描述


/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
public:
    vector<vector<int> > Print(TreeNode* pRoot) {
        vector<vector<int> > ans;
        vector<int> Temp;
        queue<TreeNode* > Q;

        if(!pRoot) return ans;
        Q.push(pRoot);
        Temp.push_back(pRoot->val);
        ans.push_back(Temp);
        
        while (Q.size()) {
            queue<TreeNode* > TQ;
            Temp.clear();
            int m = ans.size(); 
            while (Q.size()) {
                TreeNode* cur = Q.front();Q.pop();
                if(cur->left){
                    Temp.push_back(cur->left->val);
                    TQ.push(cur->left);
                }
                if(cur->right){
                    Temp.push_back(cur->right->val);
                    TQ.push(cur->right);
                }
            }
            if(Temp.size()){
                if(ans.size()%2 == 1){
                    vector<int> e;
                    for(int i=Temp.size()-1;i>=0;i--)
                        e.push_back(Temp[i]);
                    ans.push_back(e);
                }else {
                    ans.push_back(Temp);
                }
            }
                
            Q = TQ;
        }
        return ans;
    }
    
};

28 二叉树的最大深度

在这里插入图片描述

/**
 * struct TreeNode {
 *	int val;
 *	struct TreeNode *left;
 *	struct TreeNode *right;
 * };
 */

class Solution {
public:
    int awm(TreeNode* T){
        if(!T) return 0;
        return max(awm(T->left), awm(T->right)) + 1;
    }
    /**
     * 
     * @param root TreeNode类 
     * @return int整型
     */
    int maxDepth(TreeNode* root) {
        // write code here
        return  awm(root);
    }
};

29 二叉树中和为某一值的路径(一)

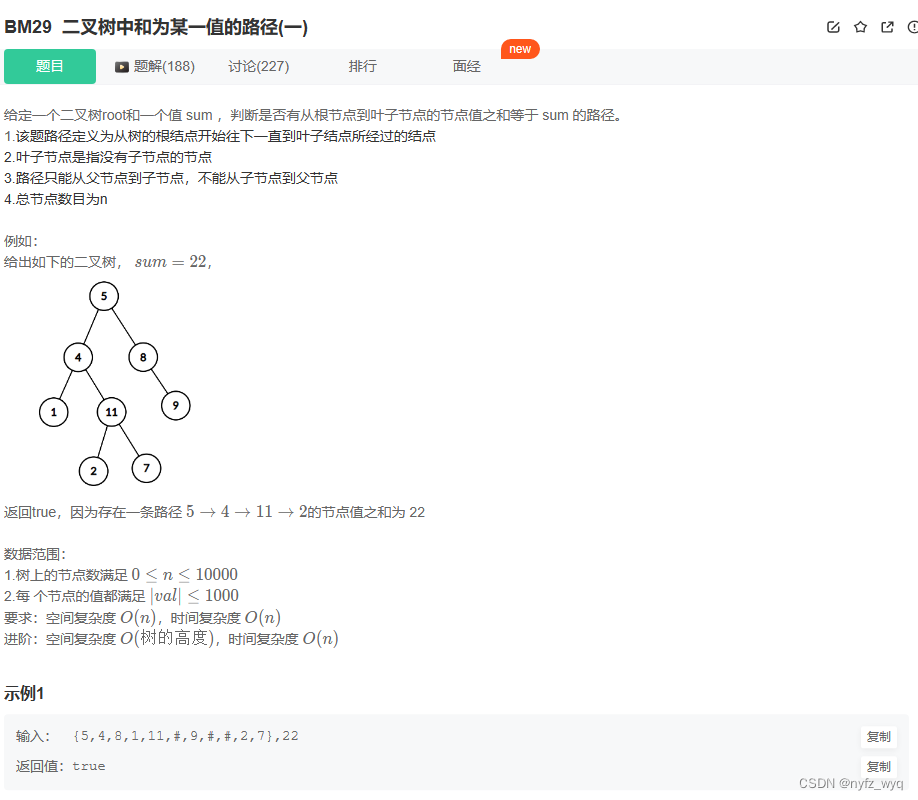
在这里插入图片描述

/**
 * struct TreeNode {
 *  int val;
 *  struct TreeNode *left;
 *  struct TreeNode *right;
 * };
 */

class Solution {
  public:
    bool awm(TreeNode* T, int sum) {
        if (!T)
            return false;
        sum -= T->val;
        if (!T->left && !T->right && sum == 0)
            return true;
        return  awm(T->left, sum) || awm(T->right, sum);
    }
    /**
     *
     * @param root TreeNode类
     * @param sum int整型
     * @return bool布尔型
     */
    bool hasPathSum(TreeNode* root, int sum) {
        // write code here

        return awm(root, sum);
    }
};

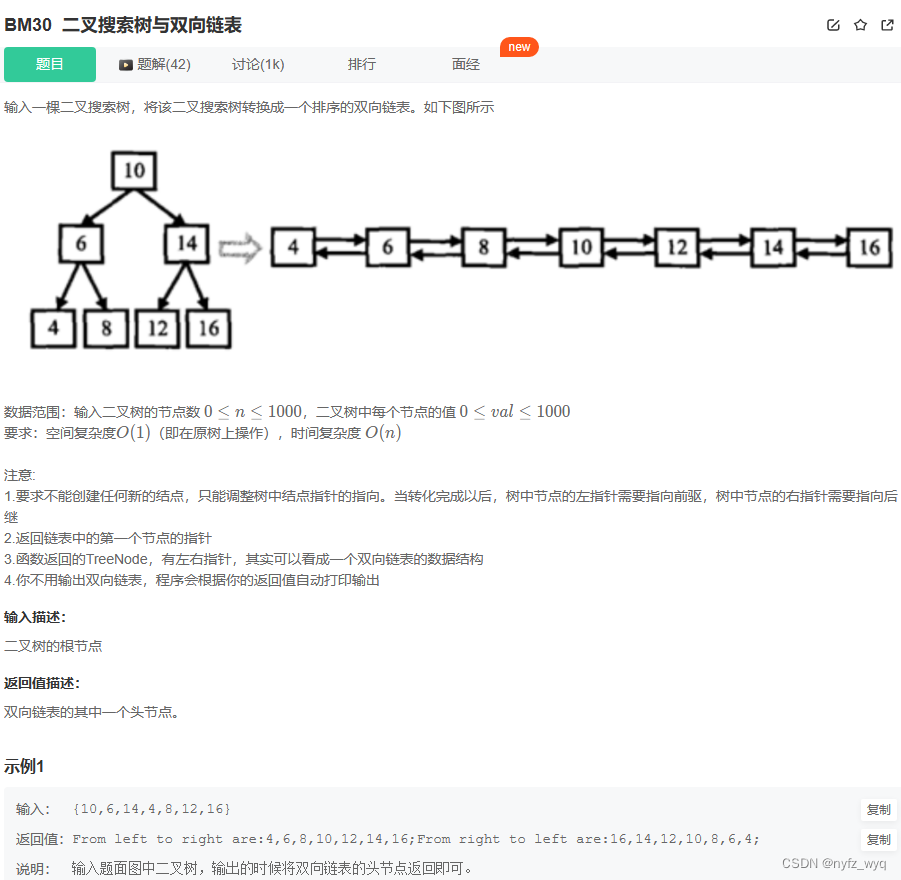
30 二叉搜索树与双向链表在这里插入图片描述

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
	TreeNode* head;
	TreeNode* pre;
    TreeNode* Convert(TreeNode* pRootOfTree) {
        if(!pRootOfTree)
			return NULL;
		Convert(pRootOfTree->left);
		if(head == NULL){
			head = pRootOfTree;
			pre = pRootOfTree;
		}else {
			pre->right = pRootOfTree;
			pRootOfTree->left = pre;
			pre = pRootOfTree;
		}
		Convert(pRootOfTree->right);
		return head;
    }
};

31 对称的二叉树

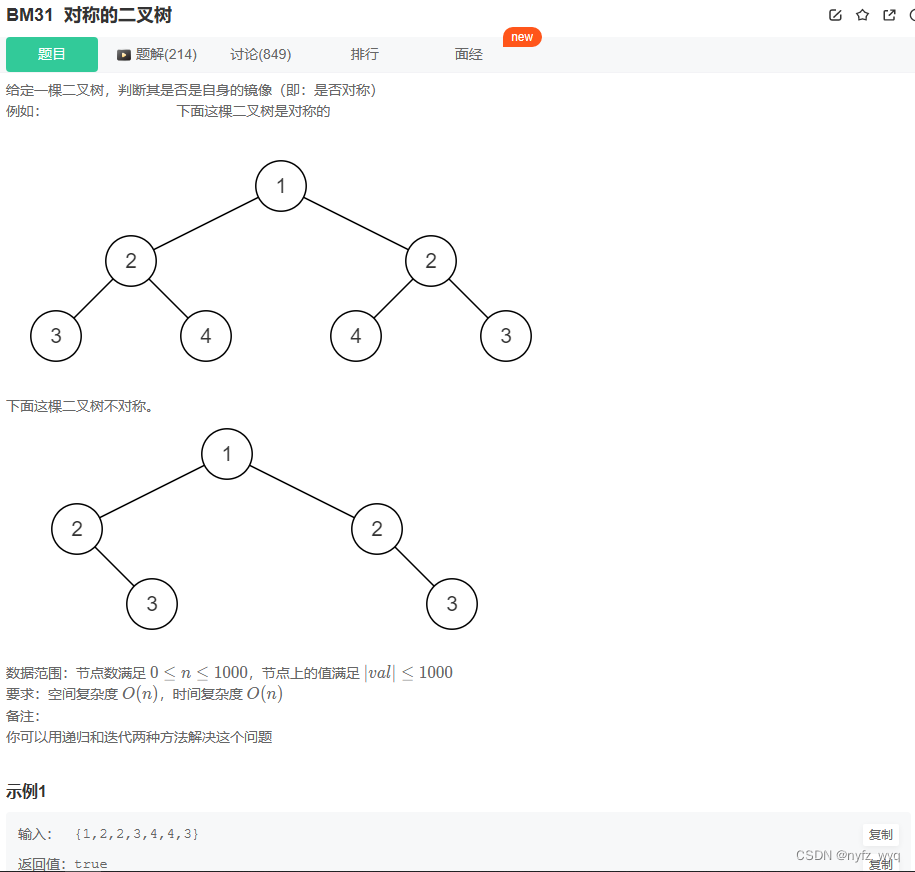
在这里插入图片描述


/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
  public:

    bool awm(TreeNode* T1,TreeNode* T2) {
        if(!T1 && !T2)
            return true;
        if(!T1 || !T2 || T1->val!=T2->val)
            return false;
        return awm(T1->left, T2->right) && awm(T1->right, T2->left);
    }
    bool isSymmetrical(TreeNode* pRoot) {
        if(!pRoot) return true;
        return awm(pRoot->left,pRoot->right);
    }

};

32 合并二叉树

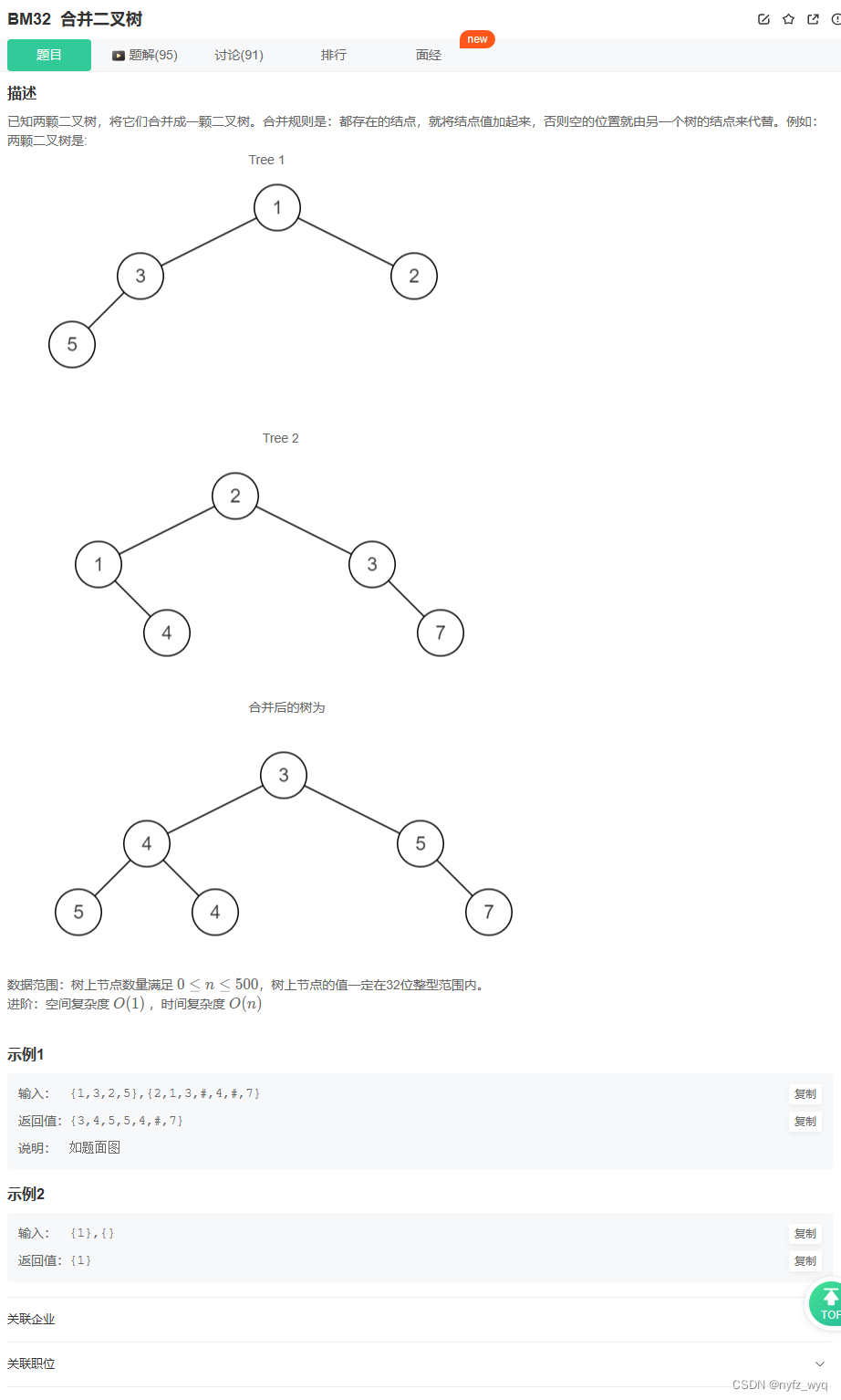
在这里插入图片描述

/**
 * struct TreeNode {
 *  int val;
 *  struct TreeNode *left;
 *  struct TreeNode *right;
 * };
 */

class Solution {
  public:
   
    /**
     *
     * @param t1 TreeNode类
     * @param t2 TreeNode类
     * @return TreeNode类
     */
    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
        // write code here
        if(!t1)
            return t2;
        if(!t2)
            return t1;
        TreeNode* node = new TreeNode(t1->val+t2->val);
        node->left = mergeTrees(t1->left, t2->left);
        node->right = mergeTrees(t1->right, t2->right);
        return node;
       
    }
};

33 二叉树的镜像

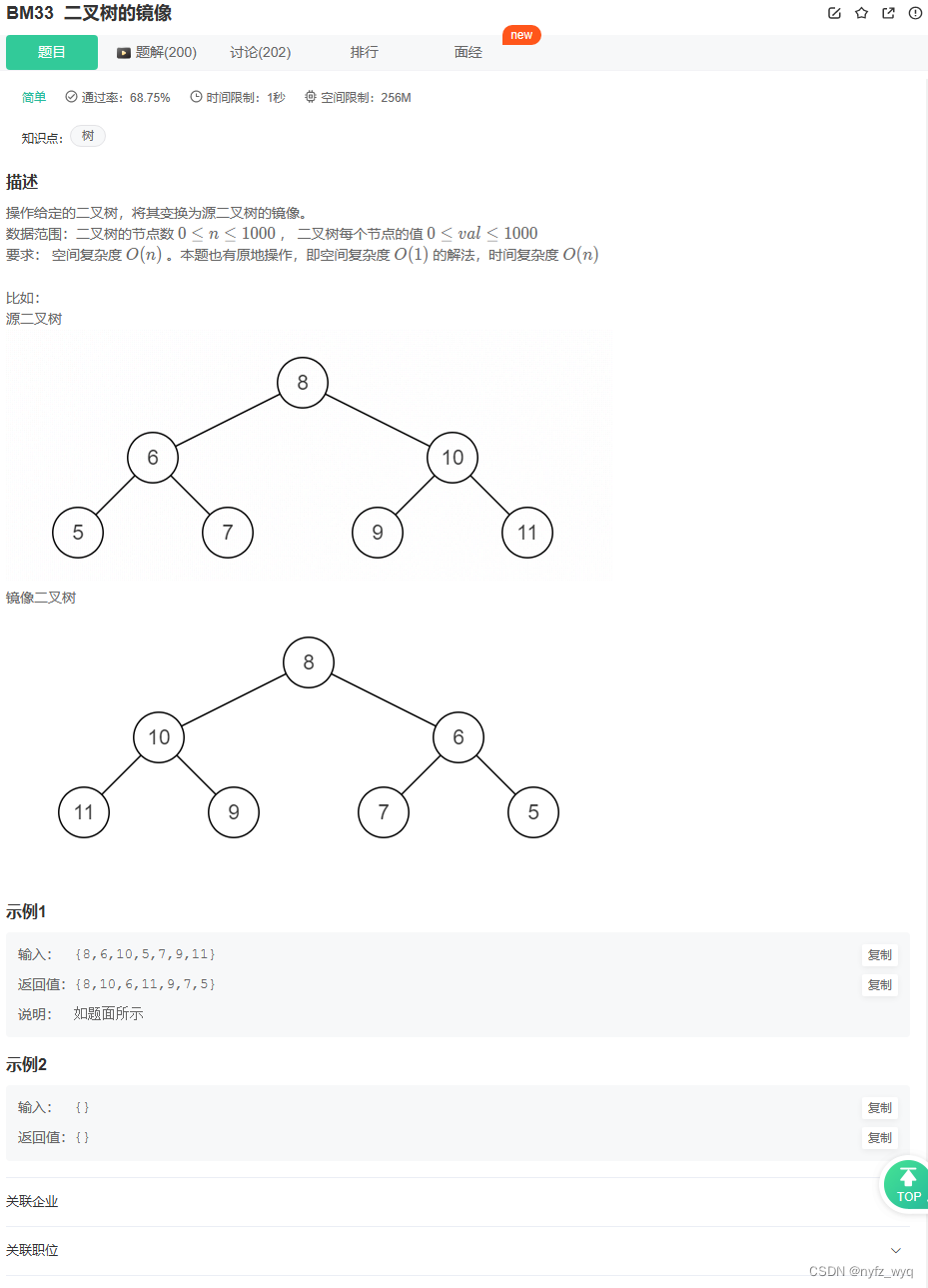
在这里插入图片描述

/**
 * struct TreeNode {
 *  int val;
 *  struct TreeNode *left;
 *  struct TreeNode *right;
 *  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
class Solution {
  public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param pRoot TreeNode类
     * @return TreeNode类
     */
    TreeNode* Mirror(TreeNode* pRoot) {
        // write code here
        if (!pRoot)
            return NULL;
        TreeNode* temp = pRoot->right;
        pRoot->right = pRoot->left;
        pRoot->left = temp;
        if (pRoot->left)
            Mirror(pRoot->left);
        if (pRoot->right)
            Mirror(pRoot->right);
        return pRoot;
    }
};

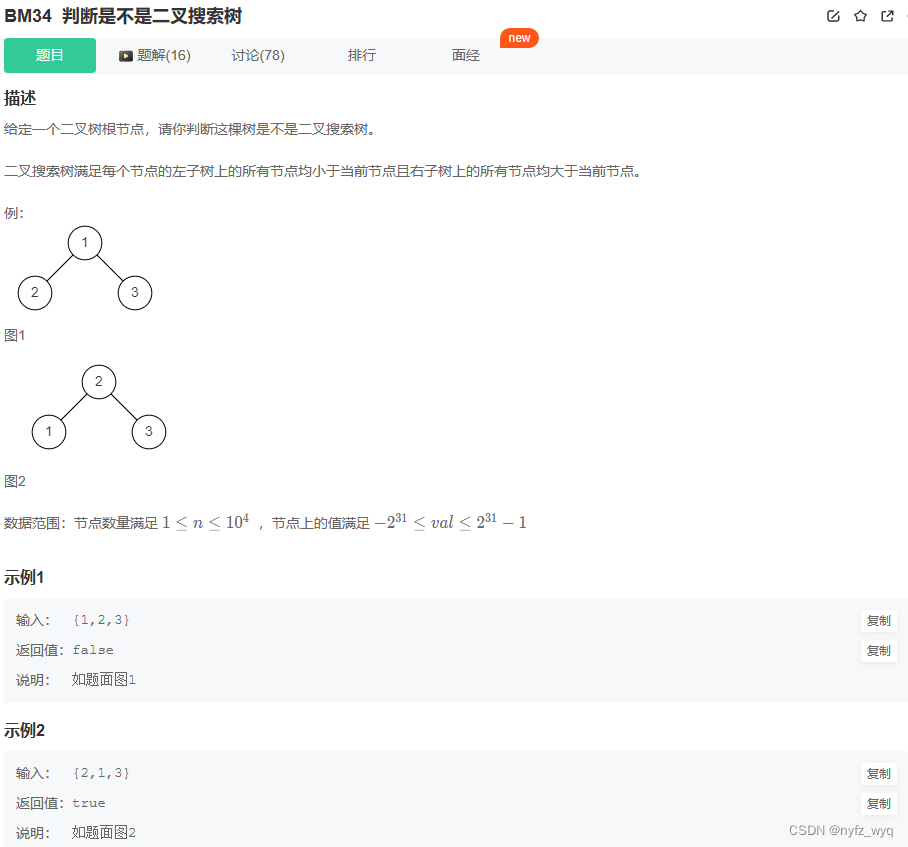
34 判断是不是二叉搜索树在这里插入图片描述

/**
 * struct TreeNode {
 *  int val;
 *  struct TreeNode *left;
 *  struct TreeNode *right;
 *  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
#include <climits>
class Solution {
  public:
    long pre = INT_MIN;
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @return bool布尔型
     */
    bool isValidBST(TreeNode* root) {
        // write code here
        if (!root) return true;
        if(!isValidBST(root->left))
            return false;
        if(root->val <= pre)
            return false;
        pre = root->val;
        if(!isValidBST(root->right))
            return false;
        return true;

    }
};

35 判断是不是完全二叉树

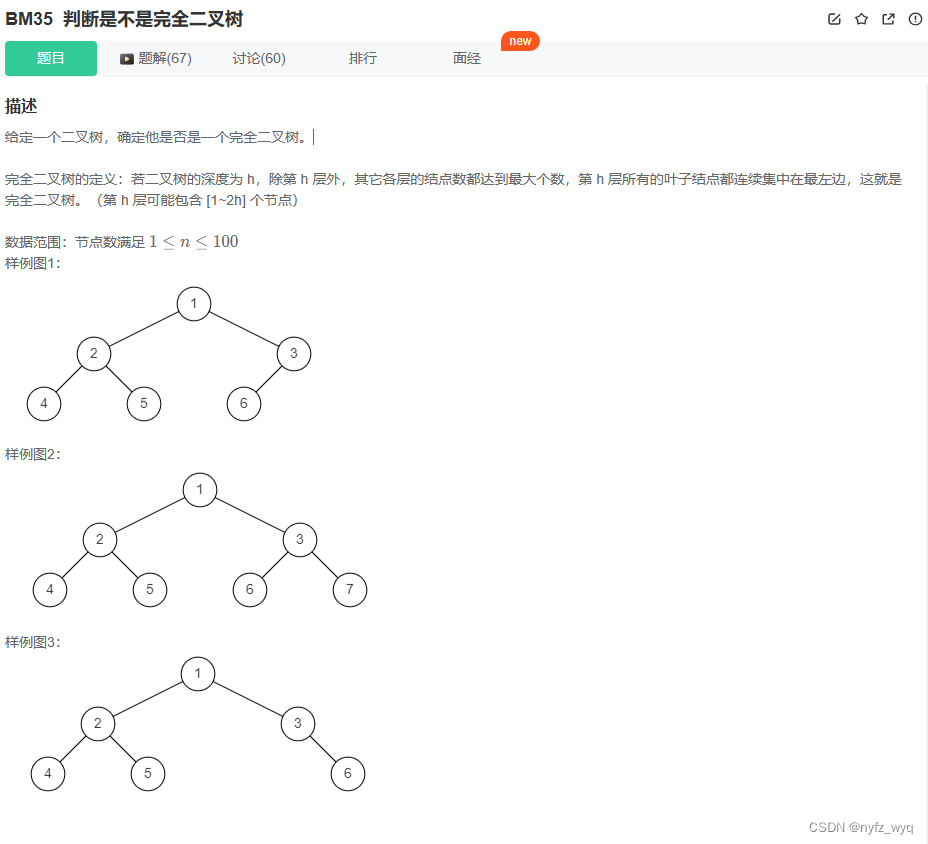
在这里插入图片描述

/**
 * struct TreeNode {
 *  int val;
 *  struct TreeNode *left;
 *  struct TreeNode *right;
 *  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
#include <queue>
class Solution {
  public:

    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @return bool布尔型
     */
    bool isCompleteTree(TreeNode* root) {
        // write code here
        if (!root) return true;
        int p = 0;
        queue<TreeNode*> Q;
        Q.push(root);
        while (Q.size()) {
            TreeNode* node = Q.front();
            Q.pop();
            if (p == 1 && node)
                return false;
            if (!node) {
                p = 1;
            } else {
                Q.push(node->left);
                Q.push(node->right);
            }


        }
        return true;
    }
};

36 判断是不是平衡二叉树

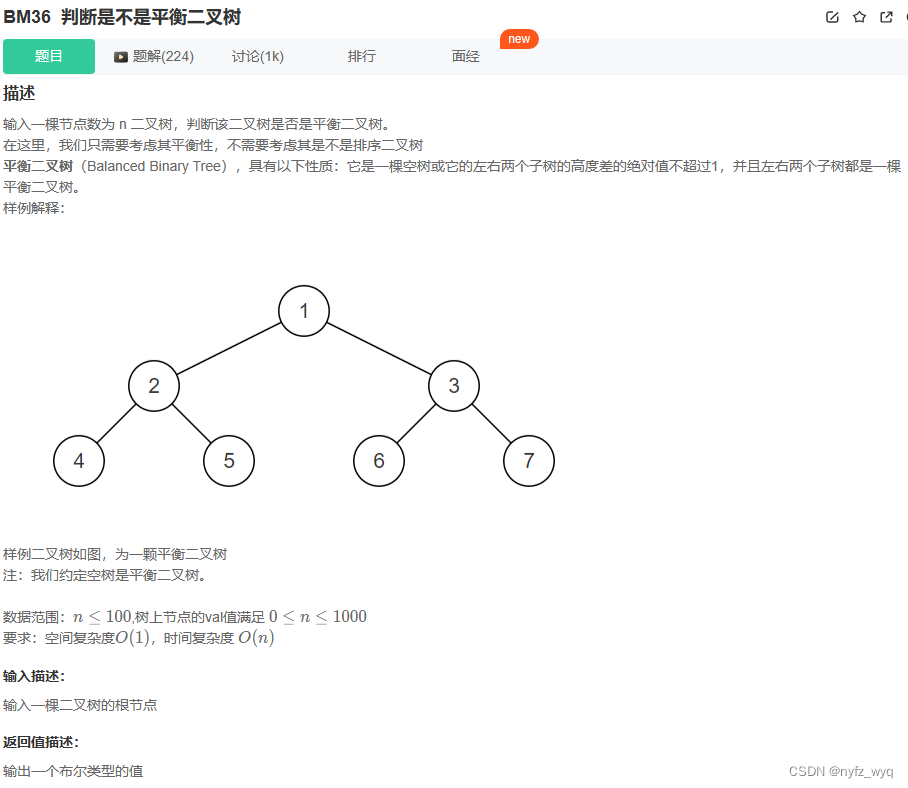
在这里插入图片描述

#include <algorithm>
class Solution {
  public:
    int awm(TreeNode* t) {
        if(!t) return 0;
        int a = awm(t->left);
        int b = awm(t->right);
        if(a==-1 || b==-1)
            return -1;
        int c = abs(a-b);
        if(c == 0 || c == 1)
            return max(a, b)+1;
        else
         return -1;
    }
    bool IsBalanced_Solution(TreeNode* pRoot) {
        int ans = awm(pRoot);
        return ans!=-1;
    }
};

37 二叉搜索树的最近公共祖先

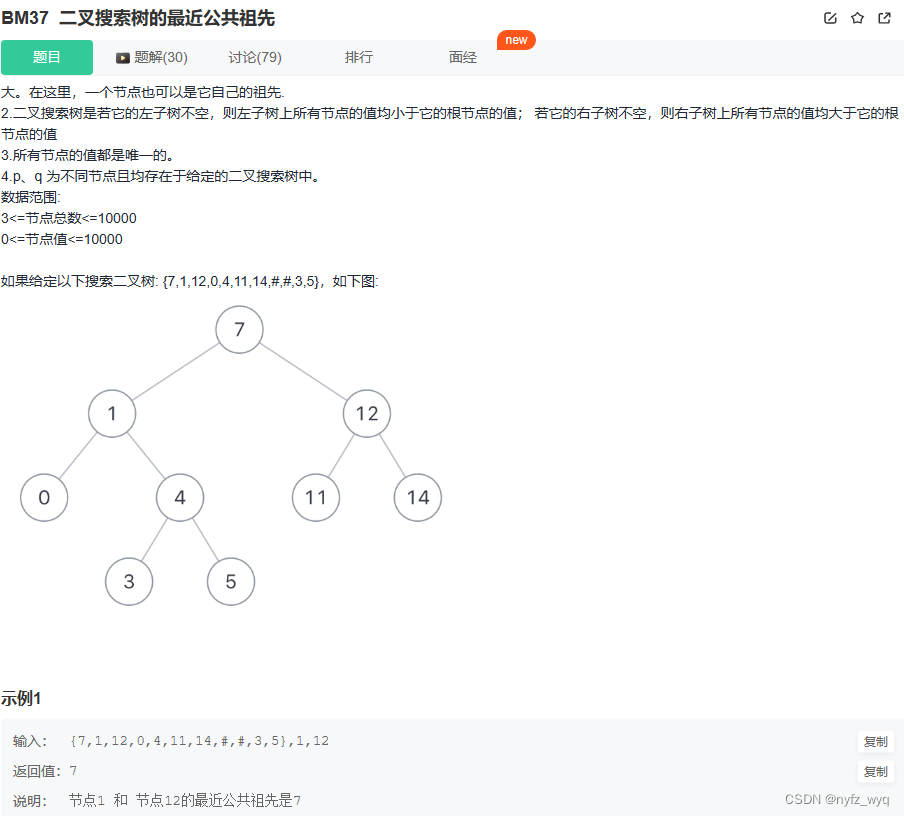
在这里插入图片描述

/**
 * struct TreeNode {
 *  int val;
 *  struct TreeNode *left;
 *  struct TreeNode *right;
 *  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
#include <algorithm>
#include <stack>
#include <vector>
class Solution {
  public:
    TreeNode* awm(TreeNode* T, int p, int q) {
        if (!T || T->val == p || T->val == q)
            return T;

        TreeNode* left = NULL;
        TreeNode* right = NULL;
        if (T->val < min(p, q)) {
            left = NULL;
        } else {
            left = awm(T->left, p, q);
        }
        if (T->val > max(p, q)) {
            right = NULL;
        } else {
            right = awm(T->right, p, q);
        }
        if (!left)
            return right;
        if (!right)
            return left;
        return T;
    }

    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @param p int整型
     * @param q int整型
     * @return int整型
     */
    int lowestCommonAncestor(TreeNode* root, int p, int q) {
        // write code here
        return awm(root, p, q)->val;
    }
};

38 在二叉树中找到两个节点的最近公共祖先

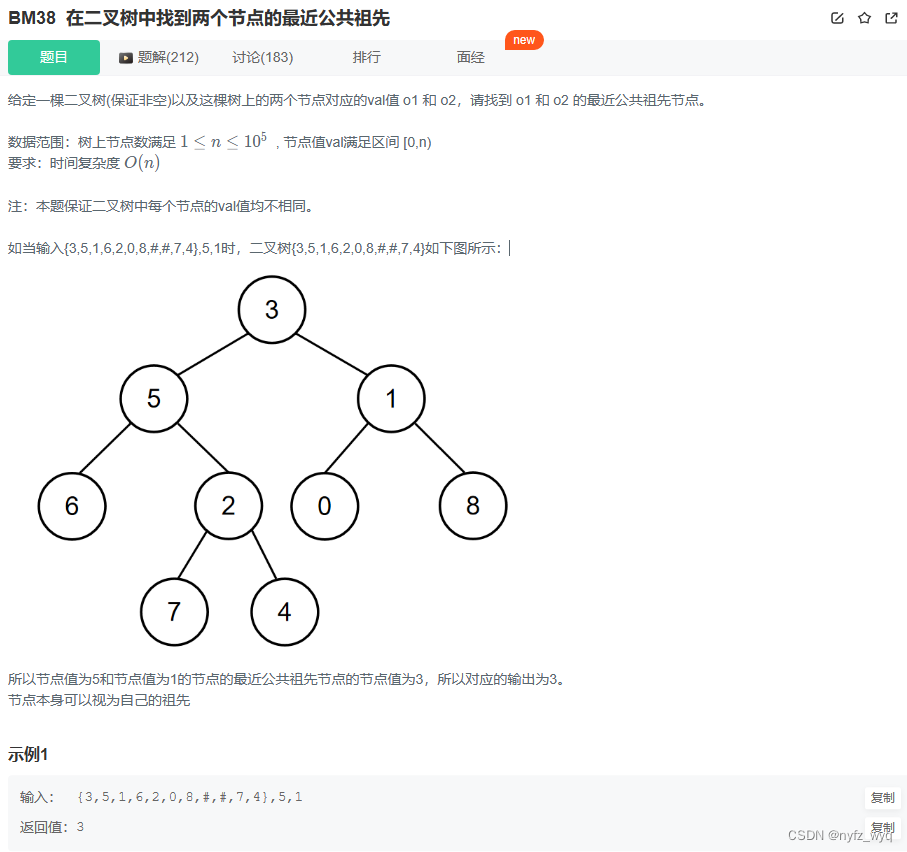
在这里插入图片描述

/**
 * struct TreeNode {
 *  int val;
 *  struct TreeNode *left;
 *  struct TreeNode *right;
 * };
 */

class Solution {
  public:

    TreeNode* awm(TreeNode* T, int o1, int o2) {
        if (!T || T->val == o1 || T->val == o2)
            return T;
        TreeNode* left = awm(T->left, o1, o2);
        TreeNode* right = awm(T->right, o1, o2);
        if(!left)
            return right;
        if(!right)
            return left;
        return T;

    }
    /**
     *
     * @param root TreeNode类
     * @param o1 int整型
     * @param o2 int整型
     * @return int整型
     */
    int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
        // write code here
        return awm(root, o1, o2)->val;
    }
};

39 序列化二叉树

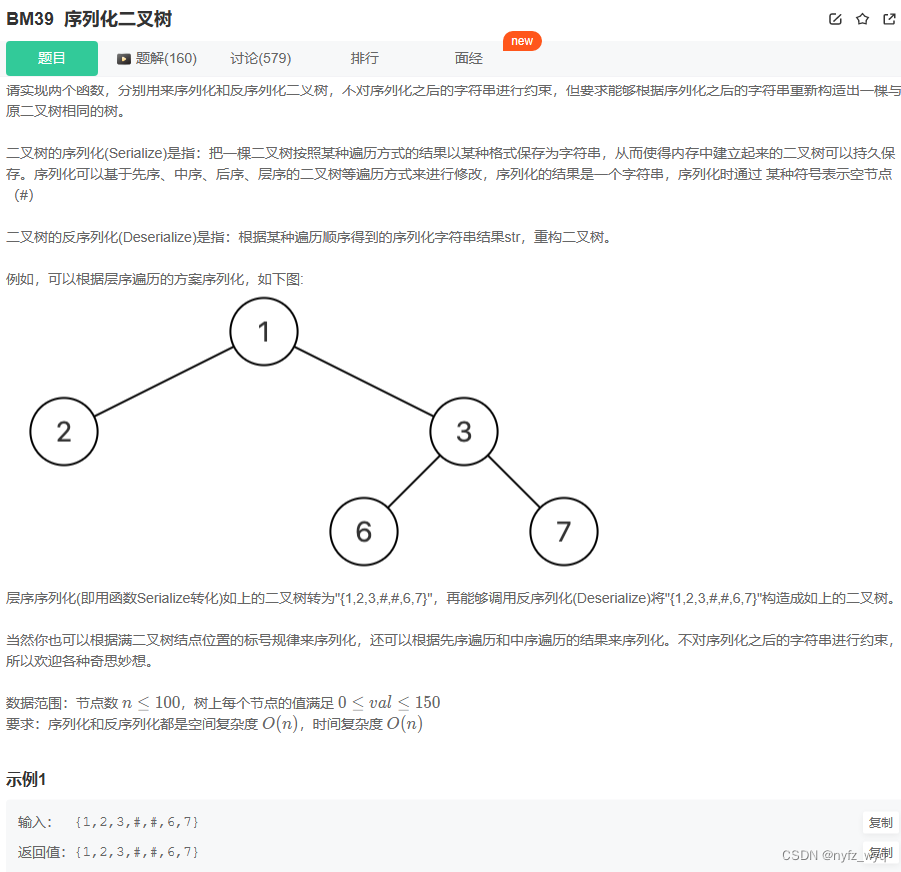
在这里插入图片描述

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
#include <cstddef>
#include <string>
#include <vector>
class Solution {
  public:
   
    char* Serialize(TreeNode* root) {
       
        if (!root) return "$";
        string ans = "";
        queue<TreeNode*> Q;
        Q.push(root);
        while (Q.size()) {
            TreeNode* node = Q.front();
            Q.pop();
            if (node) {
                ans += to_string(node->val) + "|";
                Q.push(node->left);
                Q.push(node->right);
            } else {
                ans += "#|";
            }
        }
        ans += "$";
        cout << ans << endl;
        char* C = new char[ans.length() + 1];
        strcpy(C, ans.c_str());
        C[ans.length()] = '\0';
        return C;
    }
    TreeNode* awm(int p, vector<int> V) {
        cout << V[p] << endl;
        if (V[p] == -1 || p >= V.size()) return NULL;
        TreeNode* node = new TreeNode(V[p]);
        node->left = awm(p * 2, V);
        node->right = awm(p * 2 + 1, V);
        return node;
    }
    TreeNode* Deserialize(char* str) {

        if (str[0] == '$') return NULL;
        vector<int> V;
        V.push_back(-1);
        int p = 0;

        while (str[p] != '$') {
            if (str[p] == '#') {
                V.push_back(-1);
                p++;
            } else {
                int num = 0;
                while (str[p] != '$' && str[p] != '|') {
                    num *= 10;
                    num += str[p] - '0';
                    p++;
                }
                V.push_back(num);
            }
            p++;
        }
        for (int i = 1; i < V.size(); i++) {
            if (V[i] == -1) {
                if (i * 2 < V.size()) {
                    V.insert(V.begin() + i * 2, -1);
                    V.insert(V.begin() + i * 2 + 1, -1);
                }
            }
        }

        for (int i = 0; i < V.size(); i++)
            cout << V[i] << "  ";
        cout << endl;

        return awm(1, V);
    }
};

40 重建二叉树

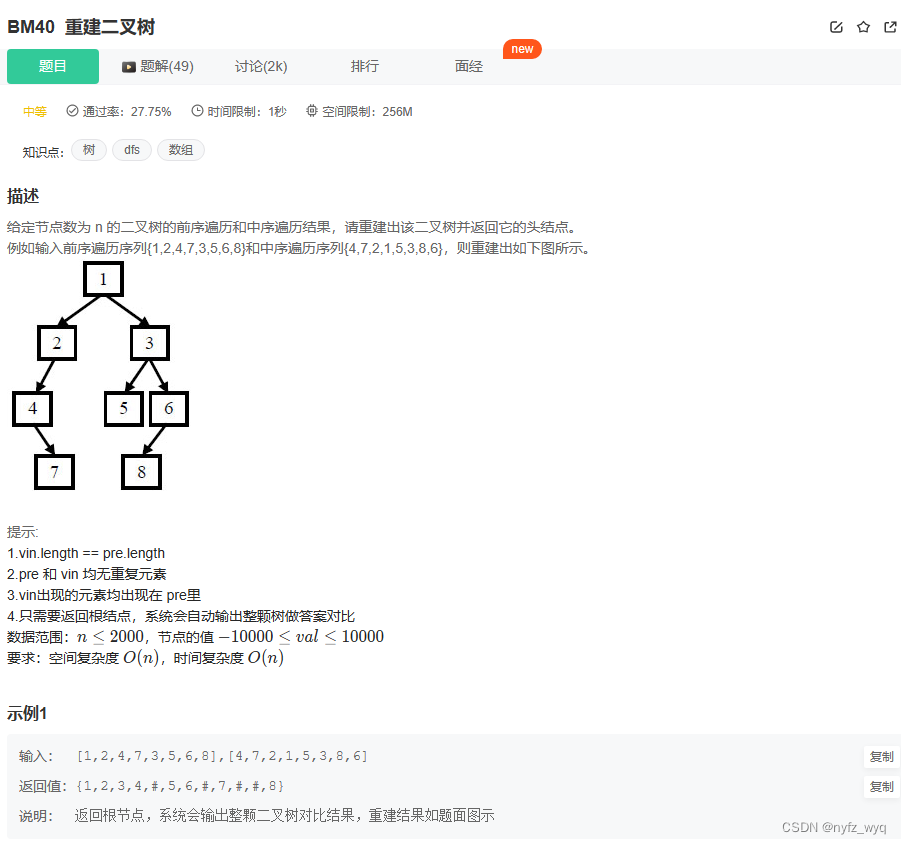
在这里插入图片描述

/**
 * Definition for binary tree
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
#include <vector>
class Solution {
  public:


    TreeNode* reConstructBinaryTree(vector<int> pre, vector<int> vin) {
        int len1 = pre.size();
        int len2 = vin.size();
        if (!len1 || !len2)
            return NULL;
        TreeNode* node = new TreeNode(pre[0]);
        for (int i = 0; i < len2; i++) {
            if (pre[0] == vin[i]) {
                vector<int> lPre (pre.begin() + 1, pre.begin() + i + 1);
                vector<int> lVin (vin.begin(), vin.begin() + i);
                node->left = reConstructBinaryTree(lPre, lVin);
                vector<int> rPre (pre.begin() + 1 + i, pre.end());
                vector<int> rVin (vin.begin() + i + 1, vin.end());
                node->right = reConstructBinaryTree(rPre, rVin);
                break;
            }
        }
        return node;
    }
};

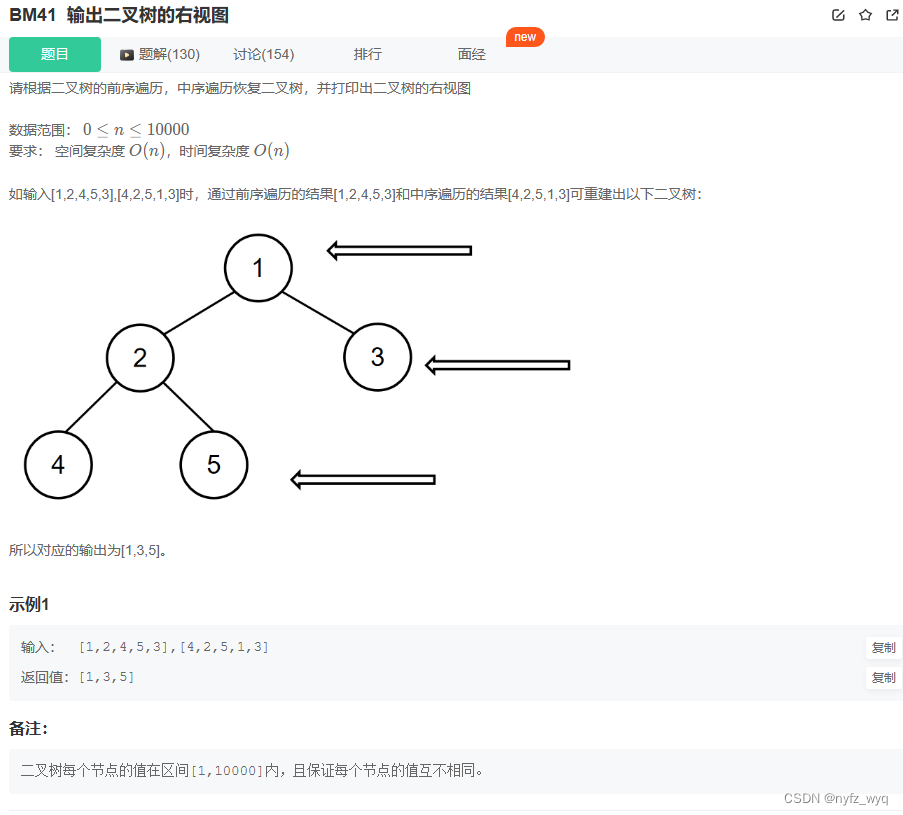
41 输出二叉树的右视图在这里插入图片描述


#include <queue>
#include <vector>
class Solution {
  public:
    TreeNode* reConstructBinaryTree(vector<int> pre, vector<int> vin) {
        int len1 = pre.size();
        int len2 = vin.size();
        if (!len1 || !len2)
            return NULL;
        TreeNode* node = new TreeNode(pre[0]);
        for (int i = 0; i < len2; i++) {
            if (pre[0] == vin[i]) {
                vector<int> lPre (pre.begin() + 1, pre.begin() + i + 1);
                vector<int> lVin (vin.begin(), vin.begin() + i);
                node->left = reConstructBinaryTree(lPre, lVin);
                vector<int> rPre (pre.begin() + 1 + i, pre.end());
                vector<int> rVin (vin.begin() + i + 1, vin.end());
                node->right = reConstructBinaryTree(rPre, rVin);
                break;
            }
        }
        return node;
    }

    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 求二叉树的右视图
     * @param xianxu int整型vector 先序遍历
     * @param zhongxu int整型vector 中序遍历
     * @return int整型vector
     */
    vector<int> solve(vector<int>& xianxu, vector<int>& zhongxu) {
        // write code here
        TreeNode* root = reConstructBinaryTree(xianxu,zhongxu);

        vector<int> ans;
        if(!root) return ans;
        queue<TreeNode*> Q;
        Q.push(root);
        
        while (Q.size()) {

            queue<TreeNode*> temp;
            while(Q.size()){
                TreeNode* node = Q.front();Q.pop();
                
                if(node->left) temp.push(node->left);
                if(node->right) temp.push(node->right);
         
                if(!Q.size()){
                    ans.push_back(node->val);
                    Q = temp;
                    break;
                }
            }

        }
        return ans;

    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/336125.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

腾讯架构师极力推荐：Java多线程与Socket实战微服务框架

腾讯架构师极力推荐：Java多线程与Socket实战微服务框架

在这个技术不断更新的年代&#xff0c;跟不上时代变化的速度就会被刷掉&#xff0c;特别是咱们程序员这一群体&#xff0c;技术不断更新的同时也要同时进步&#xff0c;不然长江后浪推前浪&#xff0c;前浪… 一个程序员从一个什么都不懂的小白在学到有一定的Java基础的时候肯…
阅读更多...
WebDAV之葫芦儿·派盘+可达漫画

WebDAV之葫芦儿·派盘+可达漫画

可达漫画 支持WebDAV方式连接葫芦儿派盘。 这是一款专为阅读你的漫画收藏而设计的阅读器。 热爱漫画的你肯定收藏了不少各种类型的漫画，它们可能有各种各样的格式，zip，rar，cbz，cbr，epub, mobi 或 pdf，也可能只是单纯的文件夹。 可达漫画支持「流式阅读」
阅读更多...
数据推荐 | 手势识别训练数据集

数据推荐 | 手势识别训练数据集

多样化&#xff0c;有按键、语音等&#xff0c;也由于整个疫情的大环境下&#xff0c;一种更方便更卫生更符合人们的非接触式交互方式—手势识别正大步发展&#xff0c;极富图像化和具备行动性的手势操作将会与人们的生活息息相关。 手势识别应用场景广泛&#xff0c;常见应用…
阅读更多...
【微电网】并网微电网运行经济性研究（Python代码实现）

【微电网】并网微电网运行经济性研究（Python代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…
阅读更多...
面试官问我：说说你对JMM内存模型的理解？为什么需要JMM?

面试官问我：说说你对JMM内存模型的理解？为什么需要JMM?

点个关注&#xff0c;必回关 随着CPU和内存的发展速度差异的问题&#xff0c;导致CPU的速度远快于内存&#xff0c;所以现在的CPU加入了高速 缓存&#xff0c;高速缓存一般可以分为L1、L2、L3三级缓存。基于上面的例子我们知道了这导致了缓存一致 性的问题&#xff0c;所以加入…
阅读更多...
字符串常量池

字符串常量池

1.创建对象的思考下面两种创建字符串的方式一样吗&#xff1f;public static void main(String[] args) {//两者一样吗String s1 "hello";String s2 "hello";String s3 new String("hello");String s4 new String("hello");System…
阅读更多...
11 Advanced CNN

11 Advanced CNN

文章目录GoogLeNetInception Module1x1 Conv计算效果代码实现总结ResNet (残差网络)问题引入梯度消失与传统神经网络的比较代码实现课程来源&#xff1a; 链接对于前篇中所提到问题&#xff0c;设计出的是一种类似于LeNet5的线性结构&#xff0c;而对于大多数问题&#xff0c;简…
阅读更多...
postgresql 数据库小版本更新

postgresql 数据库小版本更新

postgresql 数据库小版本更新 记录一次pg小版本更新 文章目录postgresql 数据库小版本更新前言一.下载最新的pg版本 pg11&#xff08;11.18&#xff09;二 pg11.5 升级 pg11.18过程1. 查看当前数据库版本&#xff1a;2. 关闭pg11.5数据库3. 安装pg11.184.修改 配置文件5. 重新…
阅读更多...
【yolov5】yolov5训练自己的数据集全流程----包含本人设计的快速数据处理脚本

【yolov5】yolov5训练自己的数据集全流程----包含本人设计的快速数据处理脚本

关于yolo应用时能用到的脚本集合&#xff0c;推荐收藏&#xff1a; https://chenlinwei.blog.csdn.net/article/details/127299428 1. 工程化快速yolo训练流程指定版&#xff08;无讲解&#xff09; 1.1 抽样数据集xml转txt输出量化分析 python make_dataset.pymake_dataset…
阅读更多...
Little Fighter：旺角——NFT 系列来袭！

Little Fighter：旺角——NFT 系列来袭！

《小朋友齐打交 2 (LF2) 》是一款流行的格斗游戏&#xff0c;由 Marti Wong 和 Starsky Wong 于 1999 年创作。这是一款非常容易上瘾的游戏&#xff0c;具有多种游戏模式、横向卷轴格斗系统以及 24 个具有复杂动作和连击的不同角色。这款游戏在世界范围内非常受欢迎&#xff0c…
阅读更多...
Debain安装命令

Debain安装命令

目录 一、安装sudo命令 二、安装jdk8 三、更换软件源 四、Debian 安装 yum 五、安装zip、unzip、curl、lrzsz、NUMA 六、安装Maven 五、问题 一、安装sudo命令 1&#xff09;执行sudo命令&#xff0c;提示 -bash: sudo: command not found的解决方法 apt-get install s…
阅读更多...
图像分割方法与问题思考

图像分割方法与问题思考

前言图像分割就是预测图像中每一个像素所属的类别或者物体。图像分割有两个子问题&#xff0c;一个是只预测类别层面的分割&#xff0c;对每个像素标出一个位置。第二个是区分不同物体的个体。应用场景&#xff0c;比如自动驾驶&#xff0c;3D 地图重建&#xff0c;美化图片&am…
阅读更多...
Docker-compose 容器集群的快速编排

Docker-compose 容器集群的快速编排

目录 一、Docker-compose 简介 二、compose 部署 2.1、Docker Compose 环境安装 三、YAML 文件格式及编写注意事项 四、Docker Compose配置常用字段 五、Docker compose 常用命令 六、案例&#xff1a;编写Docker Compose搭建lnmp论坛 6.1、配置nginx 6.2、配置mysql …
阅读更多...
Linux查看JVM FULL GC频率

Linux查看JVM FULL GC频率

查看系统的full gc频率&#xff0c;可以使用jstack命令一、采用top命令定位进程登录服务器&#xff0c;执行top命令&#xff0c;查看CPU占用情况&#xff0c;找到进程的pid二、使用jstack命令统计垃圾回收jstat -gc pid 5000即会每5秒一次显示进程号为pid的java进程的GC情况以上…
阅读更多...
PyTorch学习笔记：nn.ReLU——ReLU激活函数

PyTorch学习笔记：nn.ReLU——ReLU激活函数

PyTorch学习笔记&#xff1a;nn.ReLU——ReLU激活函数 torch.nn.ReLU(inplaceFalse)功能&#xff1a;逐元素应用ReLU函数对数据进行激活 函数方程&#xff1a; ReLU(x)(x)max⁡(0,x)ReLU(x)(x)^\max(0,x) ReLU(x)(x)max(0,x) 输入&#xff1a; inplace&#xff1a;是否改变输…
阅读更多...
C++004-C++选择与分支1

C++004-C++选择与分支1

文章目录C004-C选择与分支1条件表达式条件表达式条件表达式返回值条件语句C实现单if语句题目描述 判断奇数还是偶数题目描述 判断是否及格题目描述 判断是否为0if else语句连续if与if else的差别题目描述 输出绝对值逻辑运算符题目描述 判断程序的输出题目描述 真值表判断题目描…
阅读更多...
ElasticSearch-学习笔记04【Java客户端操作索引库】

ElasticSearch-学习笔记04【Java客户端操作索引库】

Java后端-学习路线-笔记汇总表【黑马程序员】ElasticSearch-学习笔记01【ElasticSearch基本介绍】【day01】ElasticSearch-学习笔记02【ElasticSearch索引库维护】ElasticSearch-学习笔记03【ElasticSearch集群】ElasticSearch-学习笔记04【Java客户端操作索引库】【day02】Ela…
阅读更多...
一看就会 超简单详细 ChatGPT 注册与使用攻略

一看就会 超简单详细 ChatGPT 注册与使用攻略

OpenAI 新上线的 ChatGPT 可谓是火爆出圈&#xff0c;这个语言对话模型可以回答问题&#xff0c;承认错误&#xff0c;挑战不正确的前提&#xff0c;还能帮你修改代码中的 bug…… ChatGPT 的应用场景很广泛。它可以用于处理多种类型的对话&#xff0c;包括对话机器人、问答机器…
阅读更多...
科研试剂供应1476737-97-9，Bis-PEG2-endo-BCN可发生点击反应

科研试剂供应1476737-97-9，Bis-PEG2-endo-BCN可发生点击反应

●外观以及性质&#xff1a;Bis-PEG2-endo-BCN一般为白色固体&#xff0c;BCN其为点击试剂&#xff0c;点击化学&#xff08;Click chemistry&#xff09;&#xff0c;又译为“链接化学”、“动态组合化学” &#xff08;Dynamic Combinatorial Chemistry&#xff09;、“速配接…
阅读更多...
Java面试题：Java集合框架

Java面试题：Java集合框架

文章目录一、Java集合框架二、Java集合特性三、各集合类的使用ArrayListLinkedListHashSetHashSet源码解析对源码进行总结HashSet可同步HashSet的使用HashMap四、Iterator迭代器五、遍历集合元素的若干方式参考文章&#xff1a;Hash详解参考文章&#xff1a;深入浅出学Java——…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023