1 命题
1、命题:可以判断其真值的陈述句
2、真值:真或者假(1或者0)
3、真命题:真值为真的命题
4、假命题:真值为假的命题
5、原子命题:不可以再被分解成更简单的命题
6、复合命题:由原子命题通过联结词联结而成的命题

2 命题联结词
1、五种命题联结词:否定、合取、析取、蕴含和等价
2、蕴含联结词需要注意:
p为1并且q为0 结果才为0

3、等价联结词需要注意:

4、联结词的优先顺序:
1 () 括号
2 否定
3 合取
4 析取
5 蕴含
6 等价
5、注意:原子命题

6、注意:排斥或

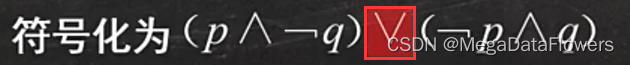
7、注意:相容或

8、注意:蕴含

1 ..., 仅当... p->q
2 仅当..., ...q->p
9、注意:等价

3 命题公式及其赋值
1、命题变元:真值可以变化的命题
2、成真赋值和成假赋值:使其对应真值为1或0
3、重言式,矛盾式和可满足式:
1 重言式(永真式):命题公式A在各种赋值下取值都为真
2 矛盾式(永假式):命题公式A在各种赋值下取值都为假
3 可满足式:**不是矛盾式**
4 题目


注意:
1 除非..., 否则... **非p->非q**

解释:
1 除非天下雨,否则他不在室内运动
2 他在室内运动,说明天下雨
3 p->q 逻辑恒等于 非p或q
4 那么 q->p表示:他在室内运动,天下雨
5 q->p 逻辑恒等于 非q或p 也就是 p或非q
6 p或非q 也就是 非p蕴含非q

每一种组合称为一种指派