一、GNN基本概念

1. 图的基本组成

图神经网络的核心就是进行图模型搭建，图是由点和边组成的。在计算机处理时，通常将数据以向量的形式进行存储。因此，在存储图时，就会有点的向量，点与点之间边的向量，全局向量（描述整张图），邻接矩阵（记录哪些点之间存在关联）等。
既然输入给计算机的是向量格式，那么embedding也是GNN中很重要的环节，即将元素进行编码

2. 邻接矩阵

邻接矩阵记录了点与点之间是否存在关联，例如：0表示无关联，1表示有关联（先这样理解，后续有算法并不这样记录）。如果图模型中有5个点，那么邻接矩阵就是一个55的对称矩阵。
当然，邻接矩阵并没有严格的定义，只要能描述元素之间的关联即可，例如，输入一段文本，邻接矩阵记录了每个单词的下一个单词是什么，如下图所示：👇

然而，在实际任务中，我们通常并不是以NN的格式构建邻接矩阵，因为不仅难以计算，而且矩阵是对称的，即浪费空间。一般地，邻接矩阵是 2*M 的格式，如下图中的Adjacency List，里面每个元素都是 source -> target的二元组，分别代表有向边的起点和终点。👇

3. 应用领域

有许多场景是无法使用传统神经网络完成的，传统的CNN、RNN、NLP等模型要求输入格式是固定的，例如图像任务要求全部的输入的shape必须是3224224等，而许多场景的格式是无法确定统一的，例如生物学中的细胞的组成等，很难套用NN module，因此GNN横空出世，给解决这类问题提出了一种新的思想。

GNN中最常见的三种任务分别是：（1）点（预测某个元素的性质）；（2）边（元素之间的关联）；（3）图（例如判定分子结构图是否存在环路）

4. Embedding & 点的更新

GNN最核心的任务就是embedding以及向量的更新【类比神经网络迭代进行parameter的更新】。GNN后续也提出了很多出色的更新点的向量的策略。下图展示了最简单的更新策略👇（例如：每次将点自身的向量 + 与之相邻的每个邻点的向量等，当然也可以在边上设置learnable参数，表征每个点对当前点的贡献程度）

5. 多层GNN & 邻接矩阵不变性

在CNN中，我们都知道，一般情况下，网络越深，epoch越大，精度越高（我说的一般！！ 勿喷）。因此，GNN通常也喜欢使用多层GNN，但是，一定注意：我们更新的是点的向量，无论怎样更新，邻接矩阵是永远不变的，有边永远都有边。👇

那么问题来啦，既然每次更新都只是考虑当前点和相邻的点，没边的永远没边，为什么要做多层？看看下图，回忆回忆神经网络👇。第0层的x₁和x₅，在第一层并没有建立联系，即x₁和x₅没有任何关系，但是再往后看一层，g₃就考虑到了x₁和x₅的特征，这也是为什么深度学习模型要深的原因之一。同样，这也是多层GNN提出的原因之一。

二、GCN（图卷积）

多数情况下，GCN是Semi - supervised Learning，即半监督学习，实际数据集中可能一部分点是没有标签的，在计算损失时只使用有标签的点计算损失。 接下来进入正题：

如上图所示，例如，将Graph输入进网络，在第一层依次对N个点进行更新，然后激活函数，第二层在刚才的基础上继续依次对N个点进行更新，以此类推，经过L（一般不太大，六度分割理论）层后，得到最终encoder得到每个点的编码向量结果。然后根据不同任务进行不同的处理。下面引出几个概念：👇

Adjacency matrix A是邻接矩阵；Matrix D是度矩阵（表征每个点有多少个邻居，一般只有对角线有元素）；Feature vector X是特征矩阵，每行表示某个点的特征编码。

为什么要引出度矩阵呢？来看一种特殊的例子，如果特征向量都是正数，则如果只进行A*X（邻接矩阵 × 特征矩阵），那么一个点的邻居越多，一般得到的数值越大，即特征越明显，这显然是不合理的（你认识的人多就有钱吗，NO）。因此引出度矩阵D，起到取平均 / 归一化的作用。👇

（这段看看就行）线性代数讲过，左乘是对行操作，右乘是对列操作，先对行做归一化，再对列作归一化，这样导致每个数参与了2次归一化，太小了，因此，折中，D^-1改为D^-1/2

三、Graph Attention Network

先来回顾一下GNN👇

以节点1的特征向量的更新为例：👇

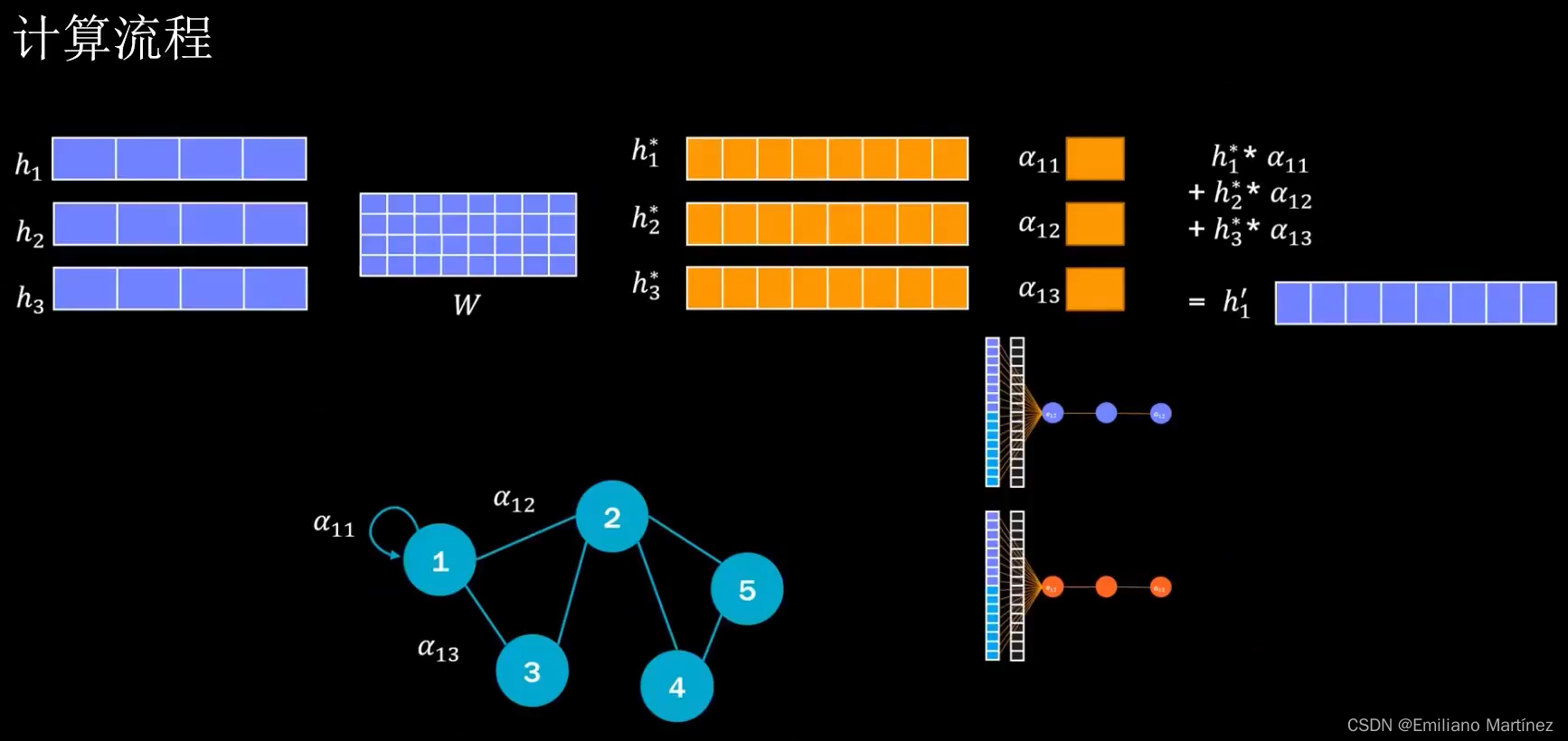
而Graph Attention Network的本质就是增加了Attention模块，即对于当前点来说，哪些点的贡献更大，哪些点的贡献更小，根据注意力机制获得的贡献程度进行更新。

那么我们如何获得边的权重呢？其中一种方式是将点1和点2的特征向量进行拼接（加入欲获取1和2之间的权重），假如shape是12N, 则构建一个2N1的可学习参数矩阵，相乘后则为权重。而获得的权重其实就是对邻接矩阵进行修改，上文提到邻接矩阵中的元素并不一定只有0和1，这里我们发现了在改进的算法中，邻接矩阵存储的是权重，因此邻接矩阵一定程度上也是可以更新的（但是有边永远还是有边，只是权重变化了）。

Graph Attention Network的计算流程如下：（1）获得每个点的编码向量，构建可学习参数矩阵W；（2）H*W获得重构后的特征；（3）获得边的贡献程度，即权重；（4）加权平均或其他算法，对每个点进行更新，即特征重构