1、删除无效的括号(广度优先搜索,字符串)
给你一个由若干括号和字母组成的字符串 s ,删除最小数量的无效括号,使得输入的字符串有效。
返回所有可能的结果。答案可以按 任意顺序 返回。
示例 1:
输入:s = "()())()"
输出:["(())()","()()()"]
示例 2:
输入:s = "(a)())()"
输出:["(a())()","(a)()()"]
示例 3:
输入:s = ")("
输出:[""]
提示:
- 1 <= s.length <= 25
- s 由小写英文字母以及括号 '(' 和 ')' 组成
- s 中至多含 20 个括号
选项代码:
class Solution:
def removeInvalidParentheses(self, s: str):
left, right = 0, 0
for c in s:
if c == "(":
left += 1
elif c == ")":
if left == 0:
right += 1
else:
left -= 1
else:
pass
def is_valid(s):
level = 0
for c in s:
if c == "(":
level += 1
elif c == ")":
if level == 0:
return False
else:
level -= 1
else:
pass
return level == 0
def dfs(s, index, left, right, res):
"""
from index to find ( or ),
left and right means how many ( and ) to remove
"""
if (left == 0) and (right == 0) and is_valid(s):
res.append(s)
return
for i in range(index, len(s)):
c = s[i]
if c in ["(", ")"]:
if (i > 0) and (c == s[i - 1]):
continue
if (c == ")") and (right > 0):
dfs(s[:i] + s[i + 1 :], i, left, right - 1, res)
elif (c == "(") and (left > 0):
dfs(s[:i] + s[i + 1 :], i, left - 1, right, res)
else:
pass
res = []
dfs(s, 0, left, right, res)
return list(set(res))
if __name__ == "__main__":
s = "(a)())()"
sol = Solution()
result = sol.removeInvalidParentheses(s) # 第一种方法,python中count()方法
print(result)2、盛最多水的容器(贪心,数组)
给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。
示例 1:
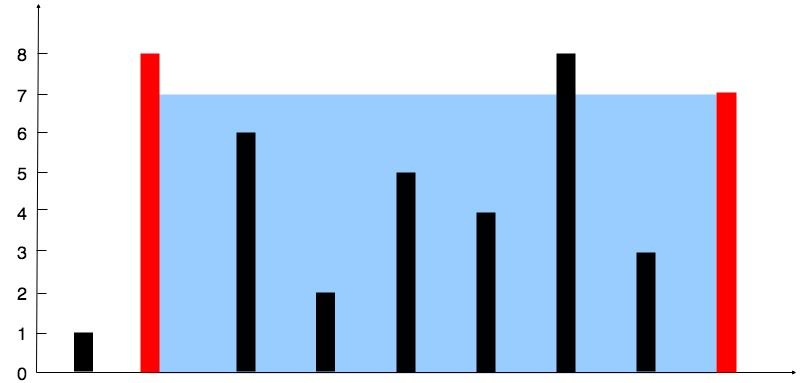
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
示例 3:
输入:height = [4,3,2,1,4]
输出:16
示例 4:
输入:height = [1,2,1]
输出:2
提示:
- n = height.length
- 2 <= n <= 3 * 104
- 0 <= height[i] <= 3 * 104
选项代码:
from typing import List
class Solution:
def maxArea(self, height: List[int]) -> int:
N = len(height)
i = 0
j = N-1
max_area = 0
while i < j:
c = (j-i)*min(height[i], height[j])
if c > max_area:
max_area = c
if height[i] > height[j]:
j -= 1
else:
i += 1
return max_area
# %%
s = Solution()
print(s.maxArea( [1,2,1]))3、搜索旋转排序数组(数组,二分查找)
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
提示:
- 1 <= nums.length <= 5000
- -10^4 <= nums[i] <= 10^4
- nums 中的每个值都 独一无二
- 题目数据保证 nums 在预先未知的某个下标上进行了旋转
- -10^4 <= target <= 10^4
进阶:你可以设计一个时间复杂度为 O(log n) 的解决方案吗?
选项代码:
class Solution:
def search(self, nums, target):
def get(start, end):
if start > end:
return -1
mid = (start + end) / 2
mid = int(mid)
if nums[mid] == target:
return mid
elif nums[mid] >= nums[start]:
if target >= nums[start] and target < nums[mid]:
return get(start, mid - 1)
else:
return get(mid + 1, end)
elif nums[mid] <= nums[end]:
if target > nums[mid] and target <= nums[end]:
return get(mid + 1, end)
else:
return get(start, mid - 1)
return get(0, len(nums) - 1)
# %%
s = Solution()
print(s.search(nums = [4,5,6,7,0,1,2], target = 0))
#4
print(s.search(nums = [4,5,6,7,0,1,2], target = 3))
#-1