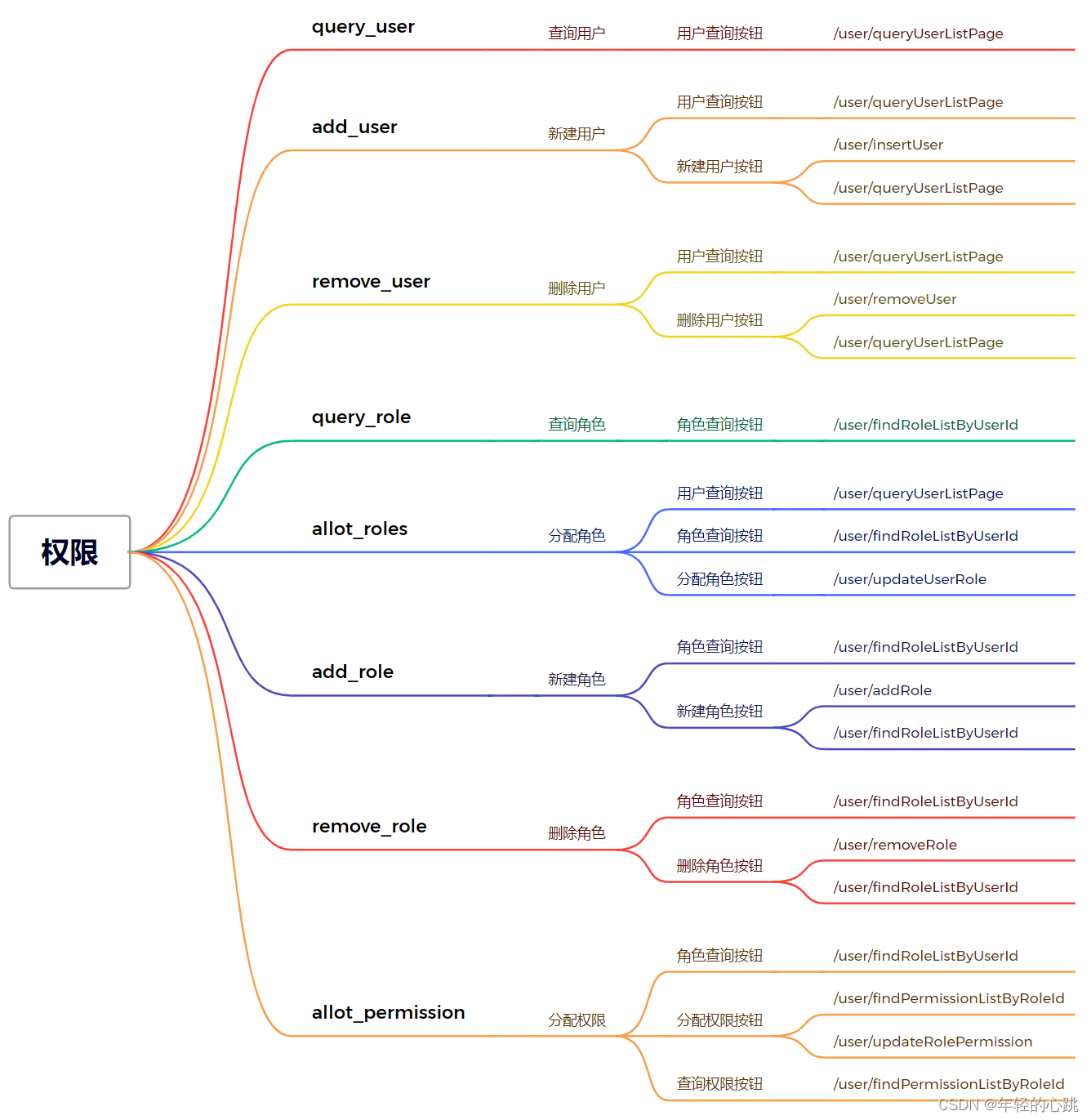
【(C语言)数据结构奋斗100天】二叉树（上）

🏠个人主页：泡泡牛奶

🌵系列专栏：数据结构奋斗100天

本期所介绍的是二叉树，那么什么是二叉树呢？在知道答案之前，请大家思考一下下列问题：

什么是二叉树的根节点？
什么是二叉树的左子树和右子树？
什么是二叉树的父节点和子节点？
二叉树的遍历有哪些方法？

让我们带着这些问题，开始今天的学习吧( •̀ ω •́ )✧

一、树和二叉树

1. 什么是树？

树是一种非线性的数据结构，是（n>=0）个节点的有限集合。当n=0时，称为空树。在任意一颗非空树中，我们可以看到节点的排列就像一颗倒着的树，根朝上，叶子朝下

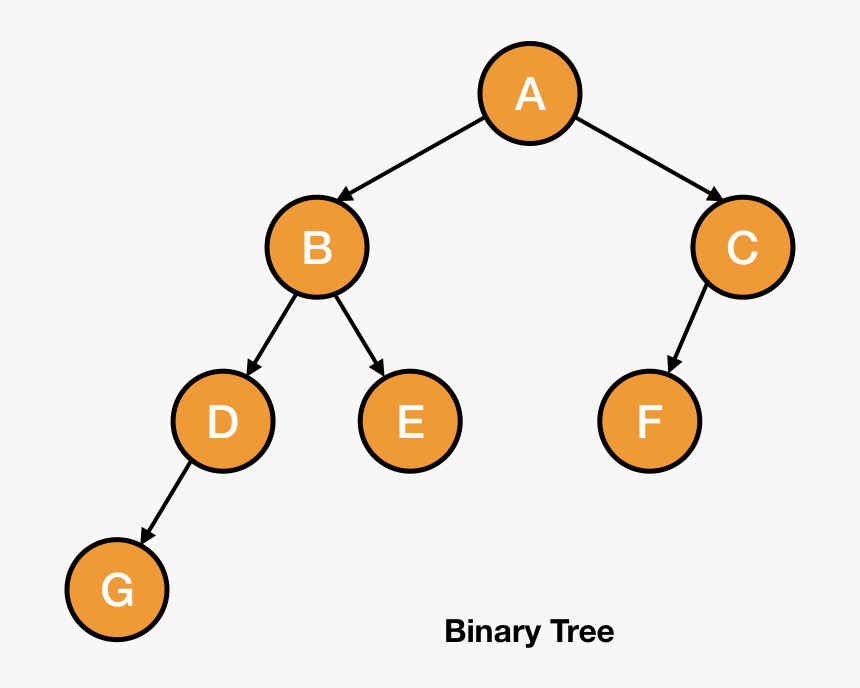
在现实生活中有哪些像上面根朝上，叶子朝下的树型结构呢🤔？

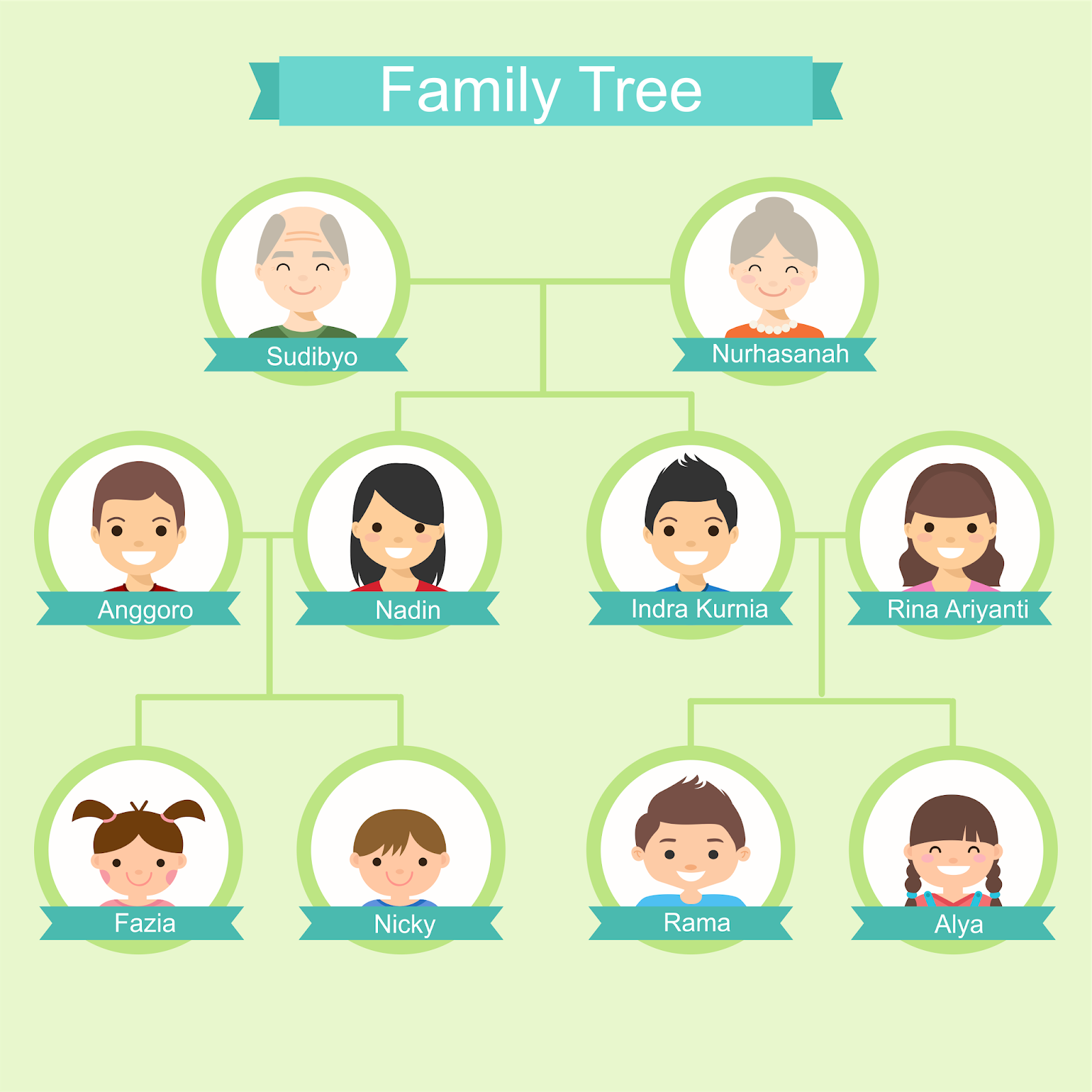
例如一个家族里组成的 “家谱” ，就是一颗树。

再例如一个阶级关系就是一颗 “树”。

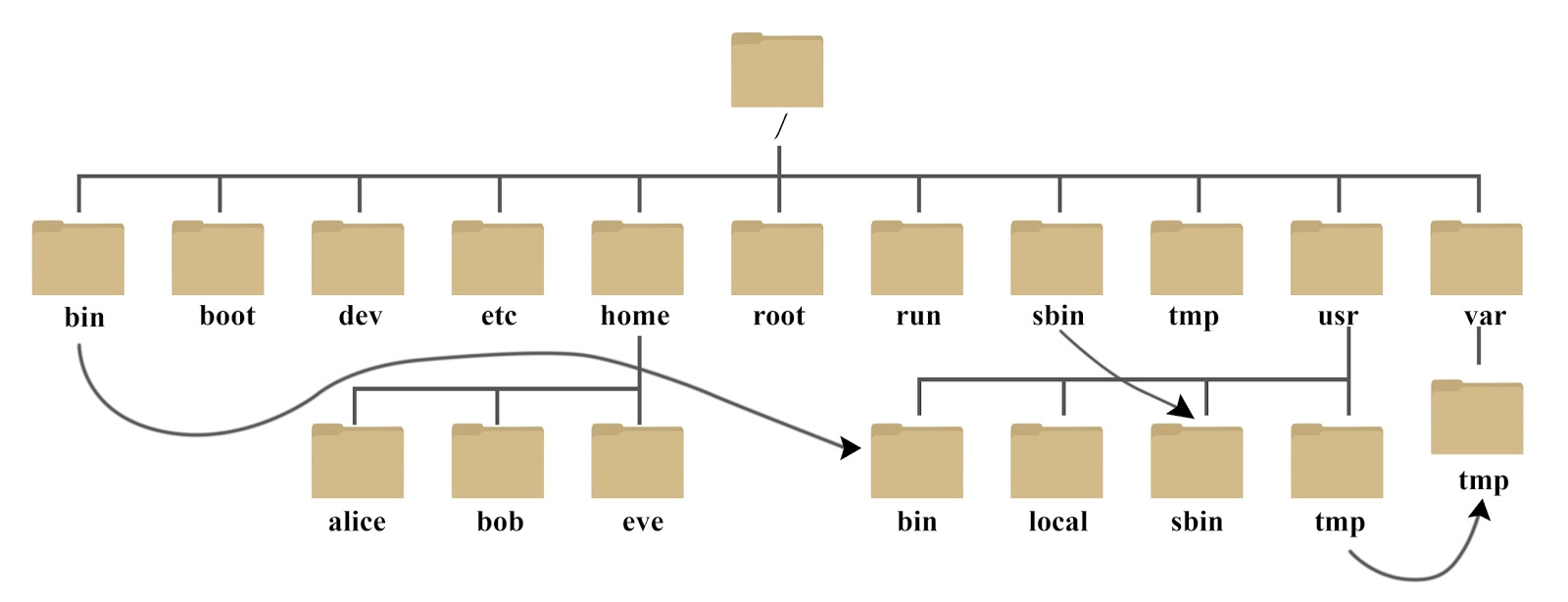
除开人与人的关系，还有很多抽象的东西也可以成为一颗 “树”，如一本书的目录，如操作系统的文件系统。

以上的共同点都是由一个 “根” 衍生出许多的 “枝干”，再从每一个 “枝干” 衍生出更多的 “叶子”。

在数据结构中，我们对树有以下称呼：

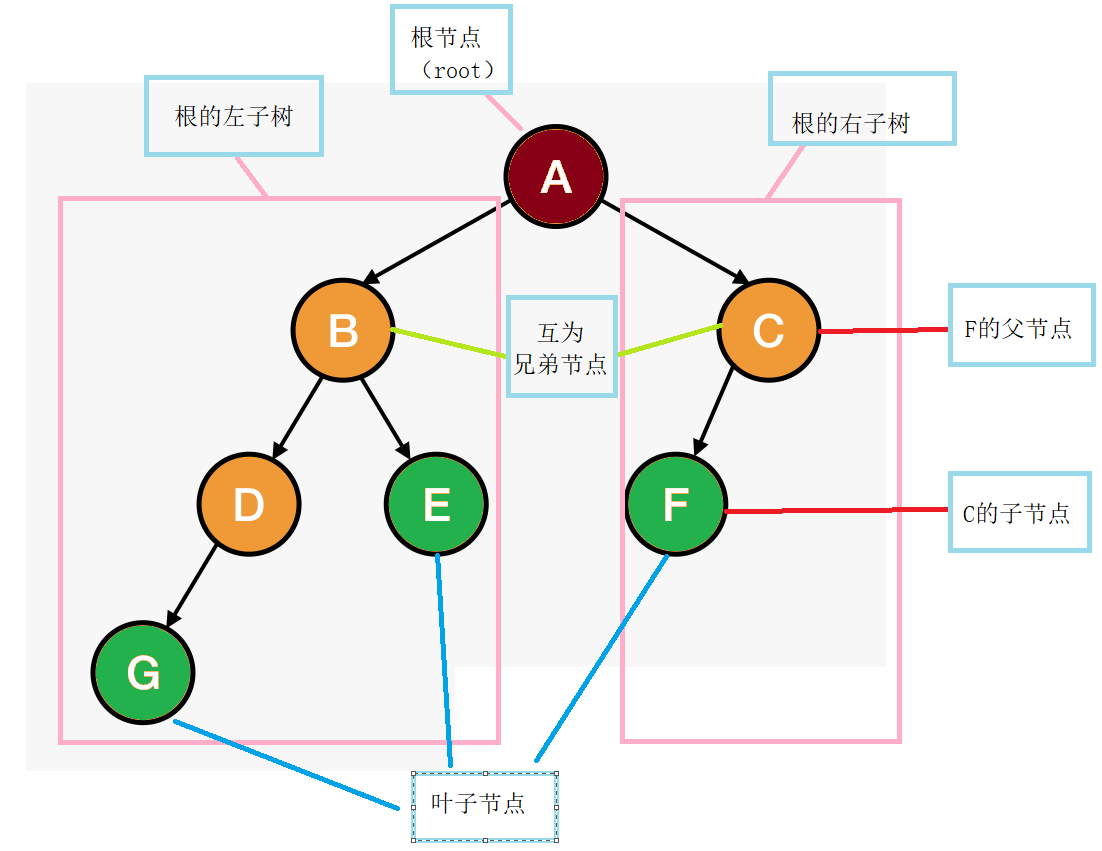
父节点/双亲节点：某节点的上一个节点为父节点，例如：C是F的父节点
(孩)子节点：某一节点指向的下一个节点为子节点，例如：F是C的子节点
兄弟节点：父节点相同的节点互为兄弟节点，例如：D、E
堂兄弟节点：双亲在同一层的节点互为堂兄弟，例如：D、F互为堂兄弟节点
节点的度：一个节点含有的子树的个数称为该节点的度，例如：B的度为2，C的度为1
叶子节点：度为0，或者无子节点的称为叶子节点，例如：G、E、F
树的度：一颗树中的最大的节点的度，例如：上图树的度为2
节点的层次：根节点为第一层，依次类推
树的高度/深度：树节点的最大层次，如上图树的高度为4
节点的祖先：根节点到此节点的经过的所有节点都为祖先，例如：A是所有节点的祖孙
子孙：只要在关系在某一节点的下面都为子孙
森林：有（m > 0）的树所组成的集合称为森林

小结：

树的关系可以由现实生活中的亲戚关系来表示

2. 什么是二叉树？

什么是 n叉树？

n叉树，故名思意，就是树的分叉最多可以有n个。

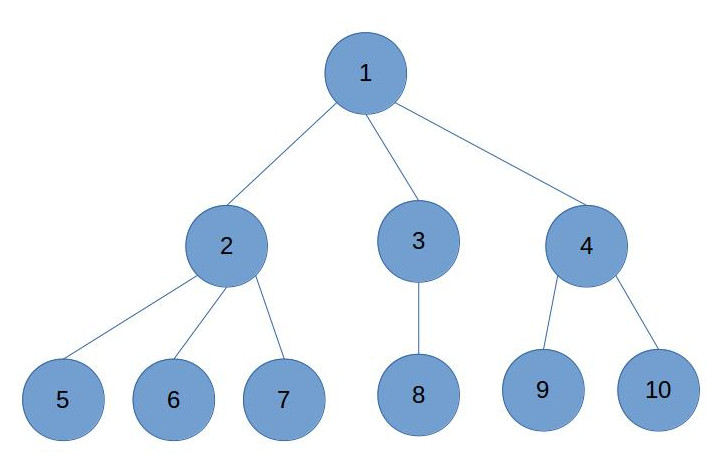
那么二叉树就是，最多有2个孩子节点的树。如下图所示。

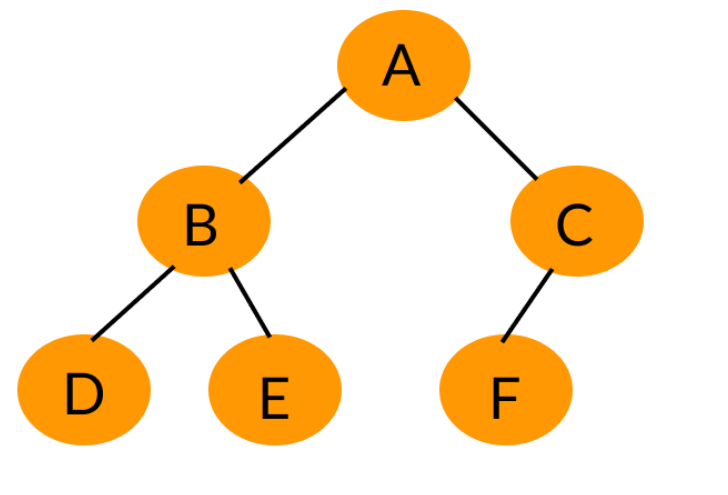
二叉树节点的两个孩子，一个被称为左孩子，一个被称为右孩子。这两个孩子的顺序是固定的。

3. 二叉树的类型

单二叉树的类型来说，其实有很多种，普通二叉树、满二叉树、完全二叉树、搜索二叉树、AVL树、红黑树……而今天我们的主题就是满二叉树和完全二叉树。

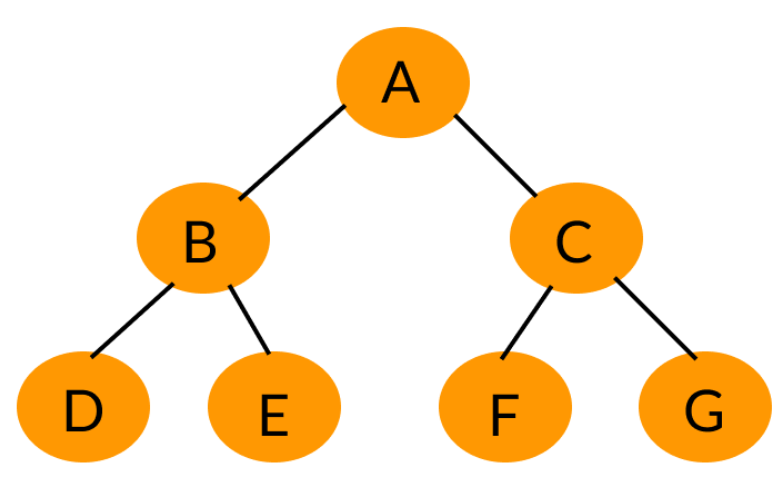
一颗二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上，那么这就是满二叉树，如下图。

满二叉树的总节点数为 $S_n = 2^{n}-1$ （n为层数）

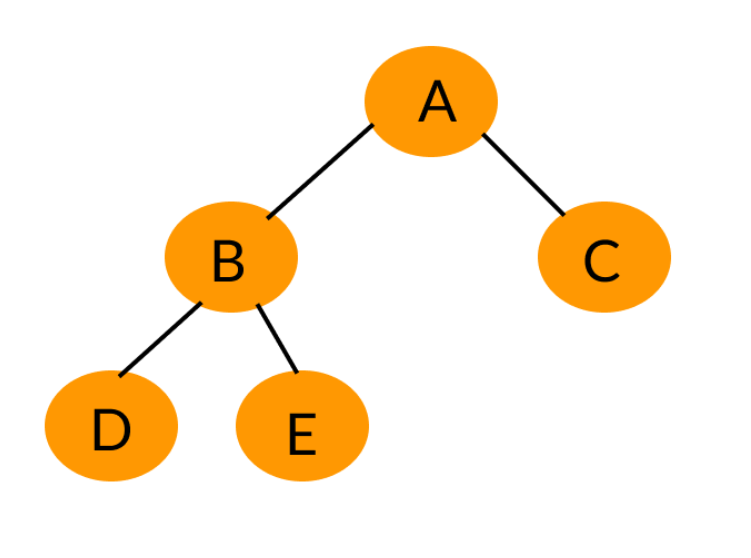
对一个有n个节点的二叉树，按层级需要编号，则所有节点编号从1到n。如果这颗树的所有节点和同样深度的满二叉树的编号为1到n的节点位置相同，则这个二叉树为完全二叉树。如下图。（简单来说，最后一层连续排布，但不满就是完全二叉树）

4. 二叉树的规律性质

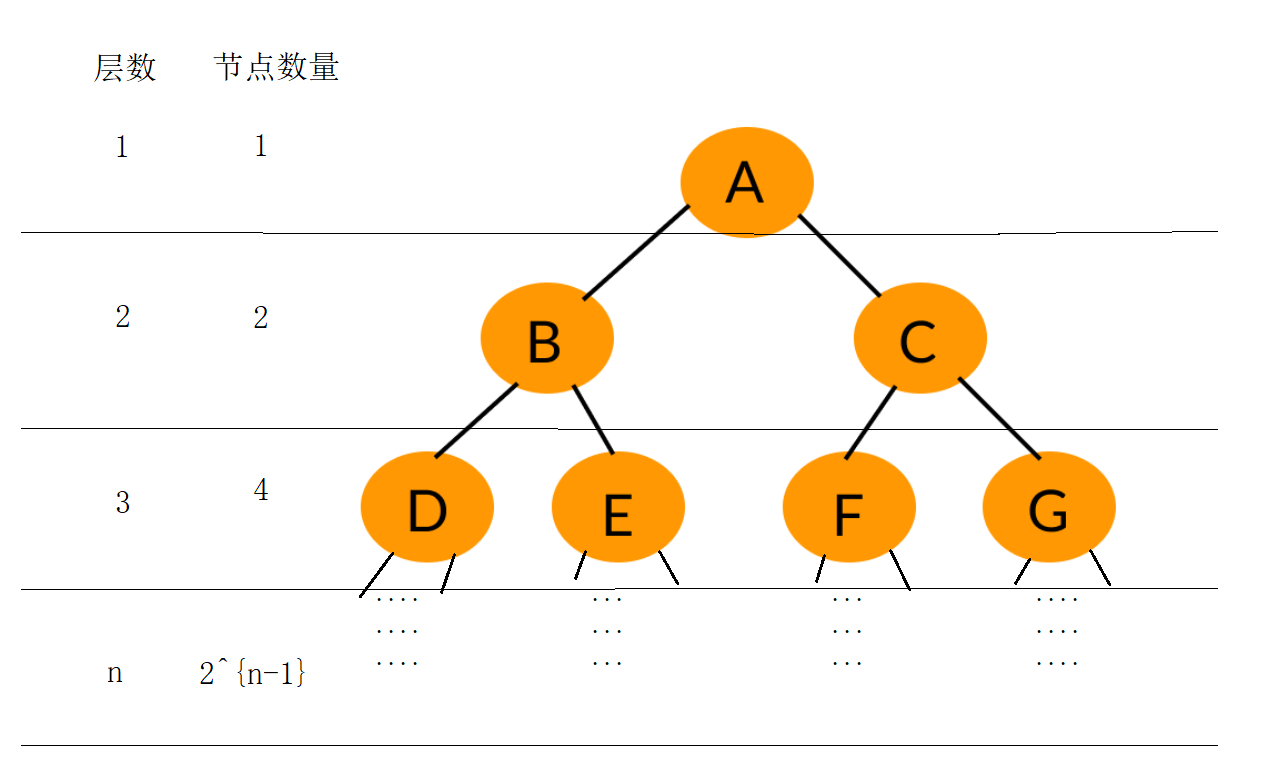
这是一个公比为2的等比数列，首项为1。即 $a_1=1$ ，公比 $q = 2$ 。
第n层节点的数量为 $2^{n-1}$ ，前n层节点的数量总和为 $S_n=2^n-1$ 。
对于任意一棵二叉树，满足 $n=n_0+n_1+n_2$ ，其中 $n$ 为节点总数， $n_0$ 表示度数为0的节点个数， $n_1$ 表示度数为1的节点个数， $n_2$ 表示度数为2的节点个数。
存在 $n_2=n_0-1$ 的关系。
计算层数 $n$ 的公式为 $n=\log_2(N+1)$ ，其中 $N$ 为节点总数。

上面这些规律往往会在刷题中使用到

二、二叉树的存储结构

链式结构和顺序结构是二叉树的两种常见存储方式。

1. 顺序结构

顺序存储结构使用数组作为基础存储单元，它适用于表示完全二叉树。除了堆，其他情况使用数组存储会则会造成大量空间浪费。顺序存储结构的二叉树在物理结构上是一个数组，逻辑结构上是一棵二叉树。

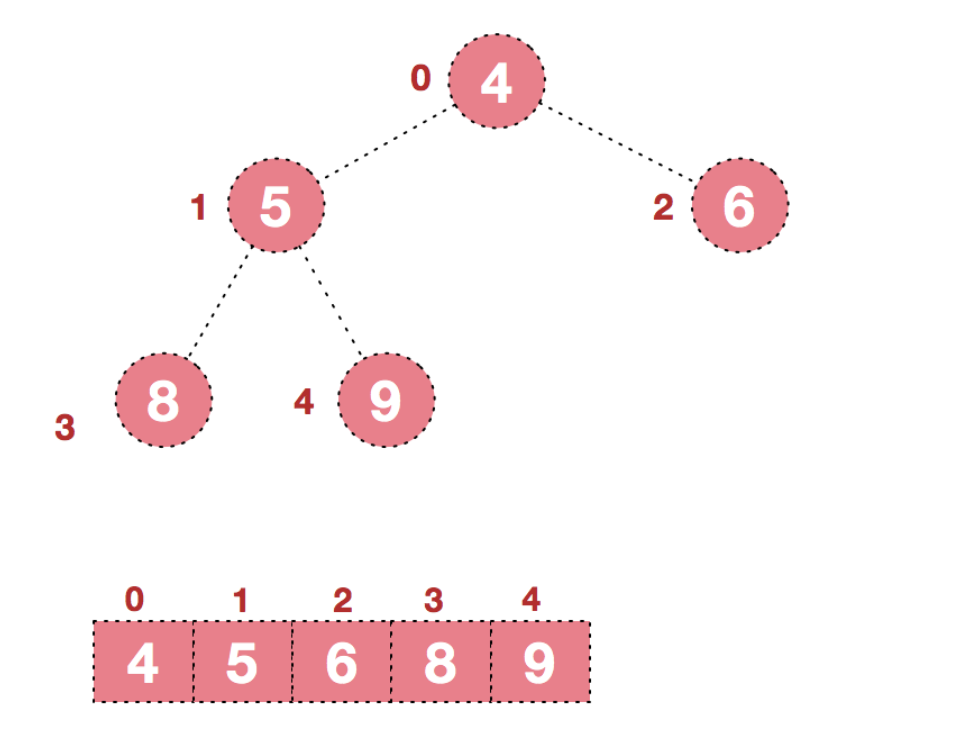
用数组来存储，我们通常会通过下标来访问元素，观察节点规律，我们不难发现：

若父节点为 father，子节点为 child，则满足：

$\frac{child - 1}{2}$
若左右子节点分别为 left 和 right，并且左右孩子都存在（即 $\ge n$ ），则满足：

$l e f t = f a t h er * 2 + 1$

$r i g h t = f a t h er * 2 + 2$

2. 链式结构

链式结构使用指针作为底层容器，通过指向子节点的指针来表示树的逻辑结构。这种方式在存储灵活性和空间利用效率方面优于顺序结构。通用方法是链表中每个节点由三个域组成：数据域和左右指针域。

typedef int treeType;//将int重定义为type_t
typedef struct TreeNode
{
    treeType val;			//表示数据
    TreeNode* left;	//表示左孩子
    TreeNode* right;	//表示右孩子
}TreeNode;

（图片）

总的来说，选择使用链式结构还是顺序结构要根据具体的存储需求来决定。

三、二叉树的遍历

当我们介绍数组、链表时，为什么没有着重研究他们的遍历过程呢？

二叉树的遍历又有什么特殊之处？

在计算机程序中，遍历线性结构的数组或链表是一件简单的事情。相反，二叉树是一种典型的非线性数据结构，遍历时需要将非线性关系的节点转化为线性序列。

二叉树的遍历可以根据节点的直接位置关系分为两类：

深度优先遍历（前序遍历、中序遍历、后续遍历）
广度优先遍历（层序遍历）

下面就来看看这些不同的遍历方式吧ο(=•ω＜=)ρ⌒☆

1. 深度优先遍历

前序遍历

二叉树的前序遍历，遍历顺序为根节点、左子树、右子树，当遇到空指针NULL时返回。

二叉树1

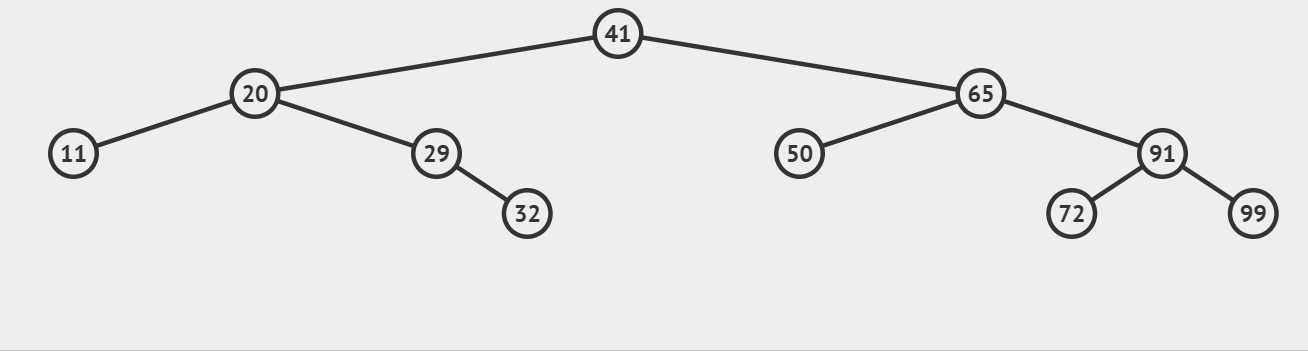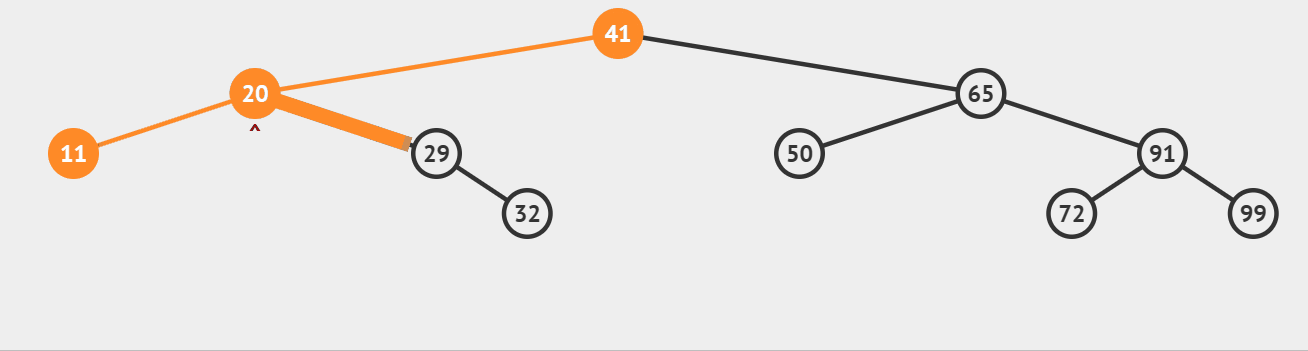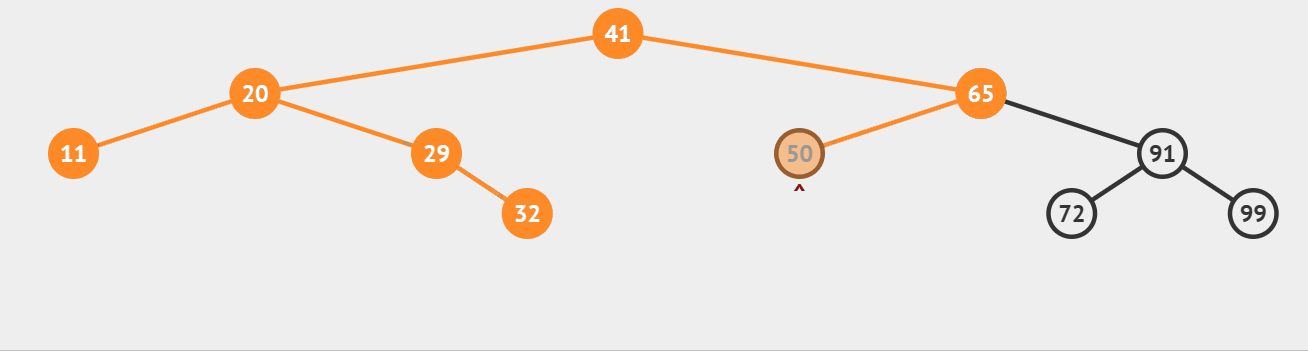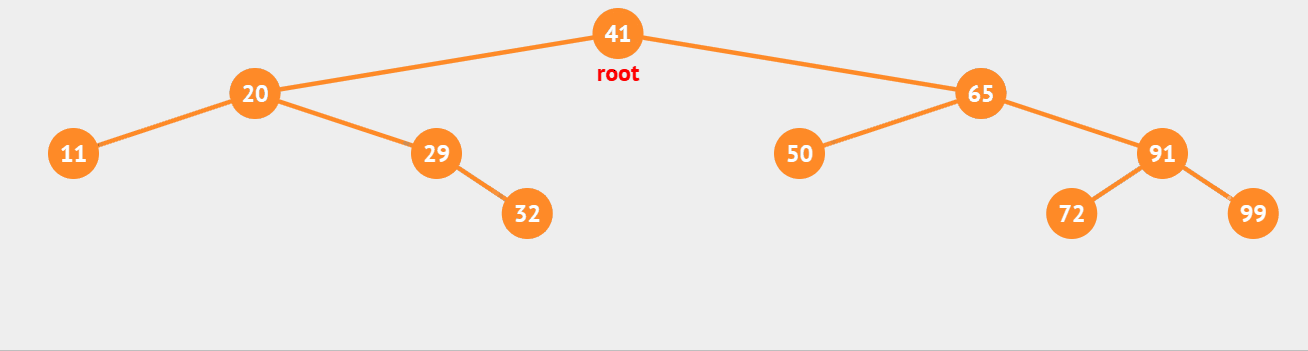
代码示例如下：

void PreOrder(TreeNode* root)
{
    if (root == NULL)
    {
        return;
    }
    //先取出当前节点元素，再对其进行相关操作
    printf("%d", root->val);
    
    InOrder(root->left);//遍历左节点
    InOrder(root->right);//遍历右节点
}

中序遍历

二叉树的中序遍历，遍历顺序为左子树、根节点、右子树，当遇到空指针NULL时返回。

二叉树2

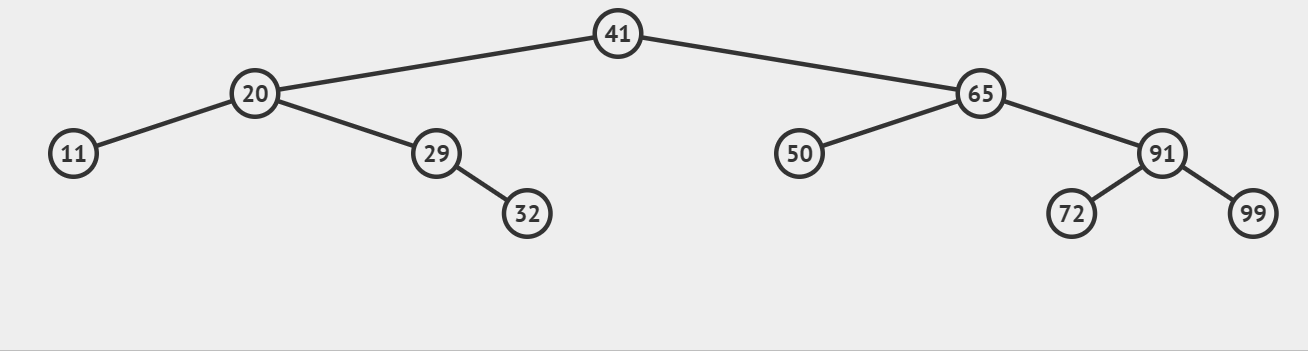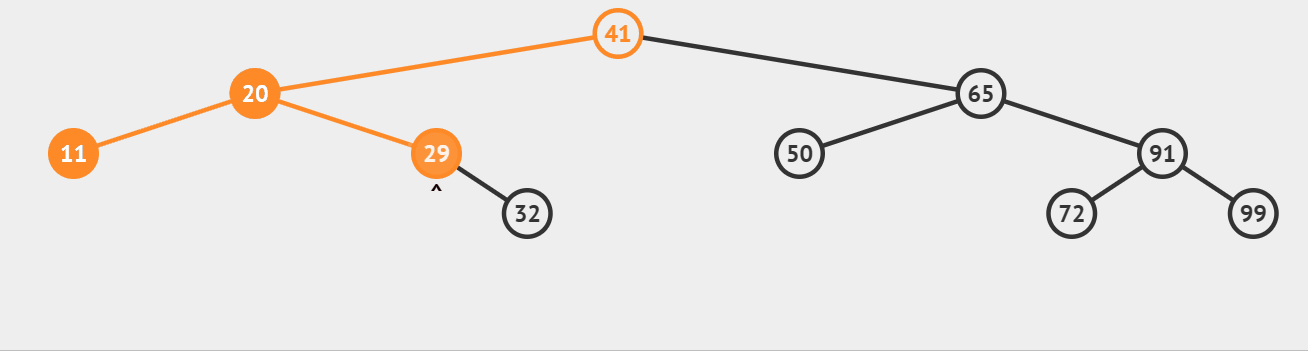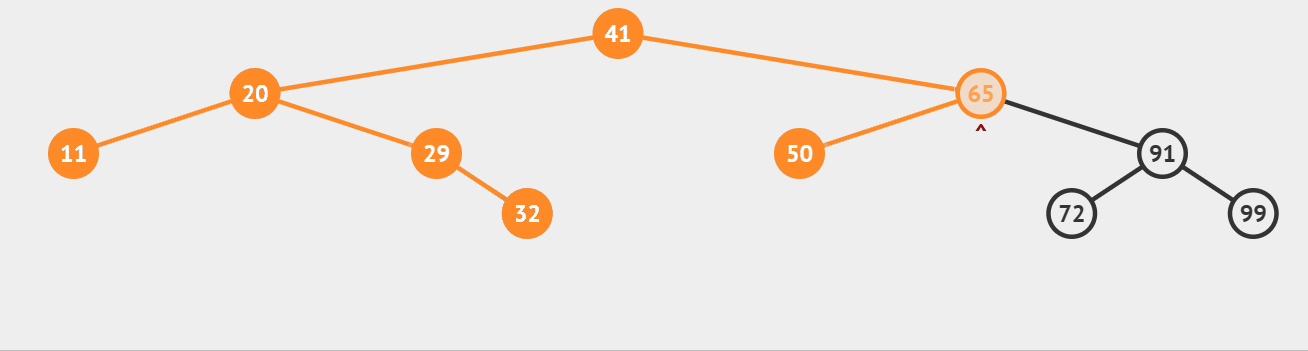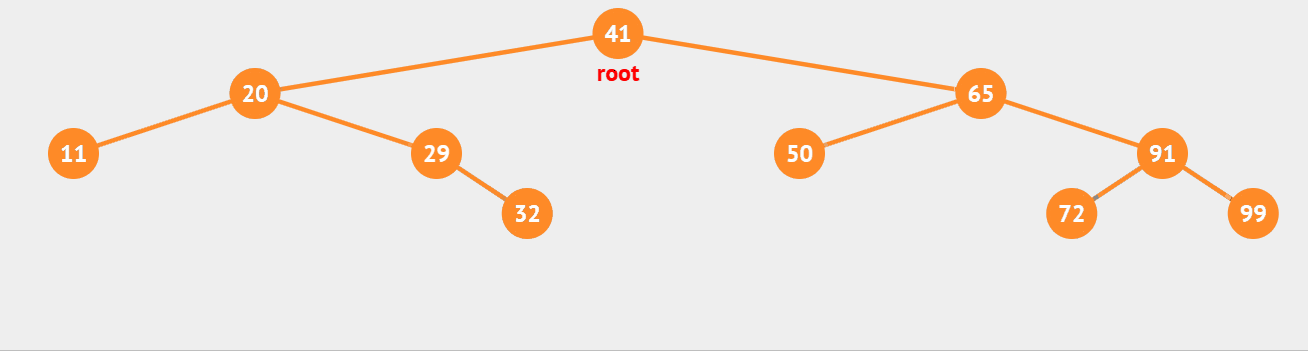
代码示例如下：

void InOrder(TreeNode* root)
{
    if (root == NULL)
    {
        return;
    }
    
    InOrder(root->left);//遍历左子树
    
    printf("%d", root->val);//取出元素，进行操作
    
    InOrder(root->right);//遍历右子树
}

后序遍历

二叉树的后序遍历，遍历顺序为左子树、右子树、根节点，当遇到空指针NULL时返回。

代码示例如下：

void PostOrder(TreeNode* root)
{
    if (root == NULL)
    {
        return;
    }
    
    PostOrder(root->left);//遍历左子树
    PostOrder(root->right);//遍历右子树
    printf("%d", root->val);//取出元素，进行操作
}

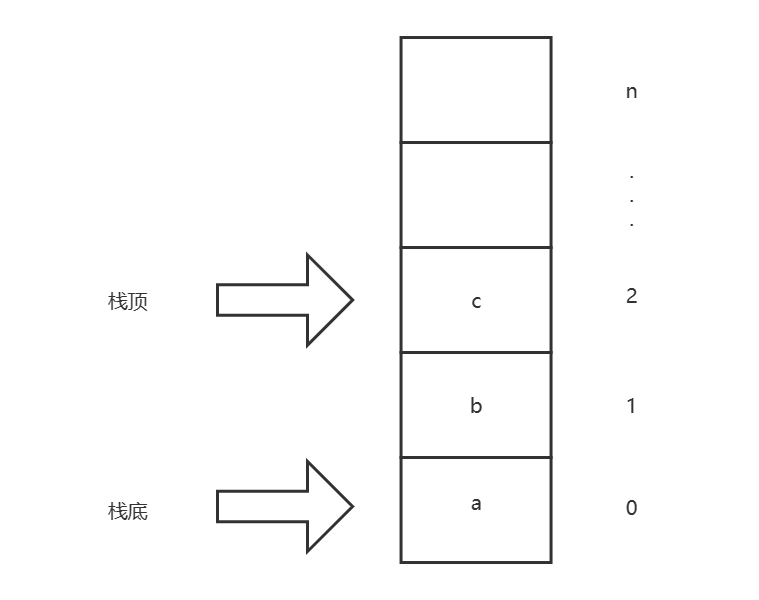
2. 广度优先遍历

广度优先遍历，按层次遍历，从根节点开始，按从上至下，从左至右的顺序遍历二叉树的所有节点。

使用广度优先算法，我们通常需要借用队列这个数据结构来实现（不知道队列的，或者没看过这篇文章的，赶紧取看看🚀传送门

接下来我们就会使用队列来完成我们所需要的操作。

这是上一期的队列节点结构，我们需要把QueueType的类型改为TreeNode*来存放我们的节点：

typedef TreeNode* QueueType;//改为TreeNode*

typedef struct QueueNode
{
    QueueType value;
    struct QueueNode* next;
}QueueNode;

而这也就是为什么我们需要对类型typedef的原因，可以方便我们做修改φ(゜▽゜*)♪

遍历代码示例如下：

void LevelOrder(TreeNode* root)
{
    Queue q;
    queue_init(&q);
    
    queue_push(&q, root);
    while (!queue_empty(&q))
    {
        TreeNode* cur = queue_front(&q);
        queue_pop(&q);
        if (cur == NULL)
        {
            continue;
        }
        printf("%d", cur->val);//取出元素，进行操作
        queue_push(&q, cur->left);
        queue_push(&q, cur->right);
    }
    
    //不要忘了释放Queue
    queue_destory(&q);
}

在刷题过程中，单纯只是这样，多半会有些不够，接下来我们就把代码进一步优化吧：

void LevelOrder(TreeNode* root)
{
    Queue q;
    queue_init(&q);
    
    int level = 0; //表示当前层数<------------
    queue_push(&q, root);
    while (!queue_empty(&q))
    {
        TreeNode* cur = queue_front(&q);
        queue_pop(&q);
        
//--------------------------------------------------
        int level_size = queue_size(&q);//获取当前层的元素个数
        for (int i = 0; i<level_size; ++i)
        {
            printf("%d", cur->val);//取出元素，进行操作
            
            //对当前节点的左右子节点进行判断，若为空便没有必要入队列
            if (cur->left != NULL)
            {
                queue_push(&q, cur->left);
            }
            if (cur->right != NULL)
            {
                queue_push(&q, cur->right);
            }
        }
//---------------------------------------------------
        
        ++level;//层数+1 <------------
    }
    
    //不要忘了释放Queue
    queue_destory(&q);
}