【后续会持续更新CDA Level I&II备考相关内容，敬请期待】

【考试大纲】

【考试内容】

【备考资料】

【扩展知识——大数定律和中心极限定理】

大数定律和中心极限定理

3、统计分布

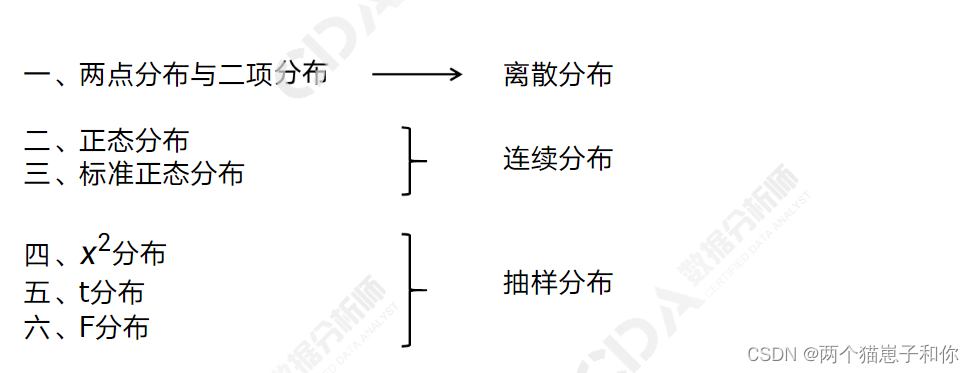
3.1、离散型随机变量的三种重要分布

3.1.1、两点分布

两点分布又叫伯努利分布，指的是对于随机变量X有, 参数为p(0<p<1)，如果它分别以概率p和1-p取1和0为值。EX= p,DX=p(1-p)。伯努利试验成功的次数服从伯努利分布,参数p是试验成功的概率。伯努利分布是一个离散型机率分布，是N=1时二项分布的特殊情况，为纪念瑞士科学家詹姆斯·伯努利(Jacob Bernoulli 或James Bernoulli)而命名。

3.1.2、伯努利试验及二项分布

3.1.2.1、伯努利试验

3.1.2.2、二项分布

3.1.3、泊松分布

3.2、离散型随机变量的分布函数

3.2.1、分布函数的定义

3.2.2、分布函数的性质

3.3、连续型随机变量及其概率密度

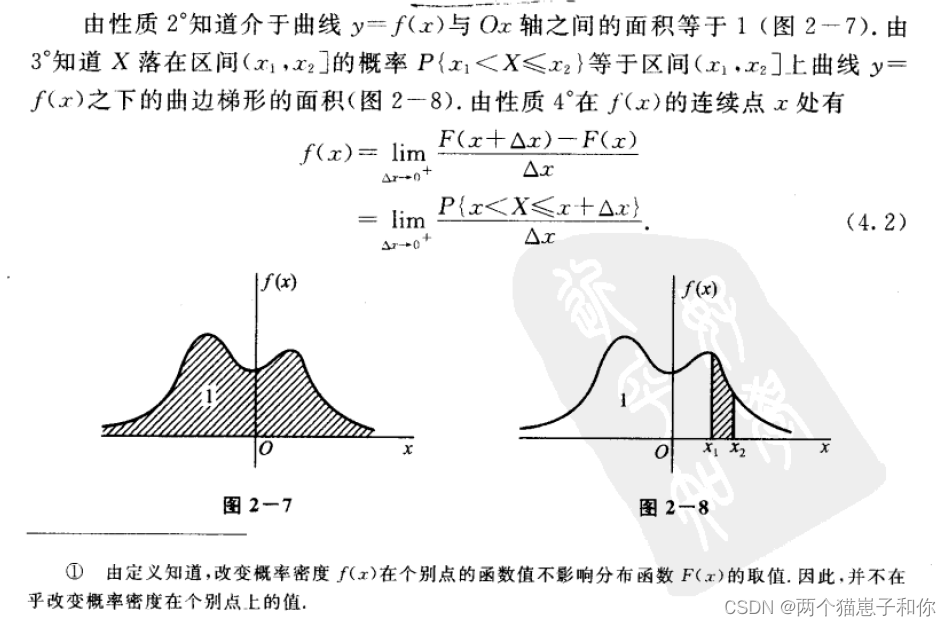
3.4、连续性随机变量的三种重要分布

3.4.1、均匀分布

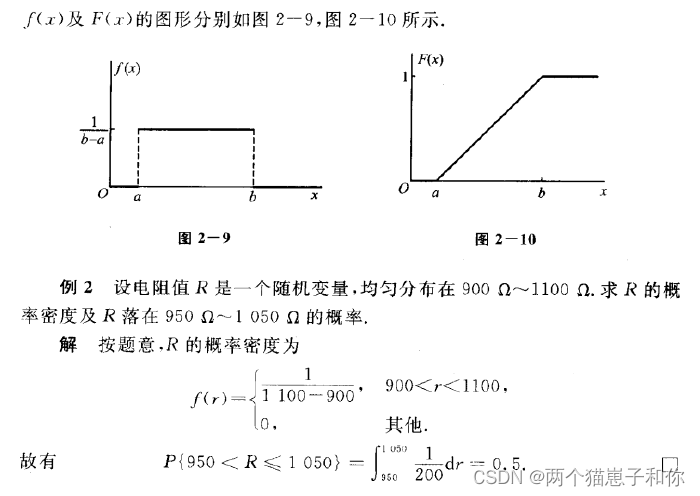
3.4.2、指数分布

3.4.3、正态分布

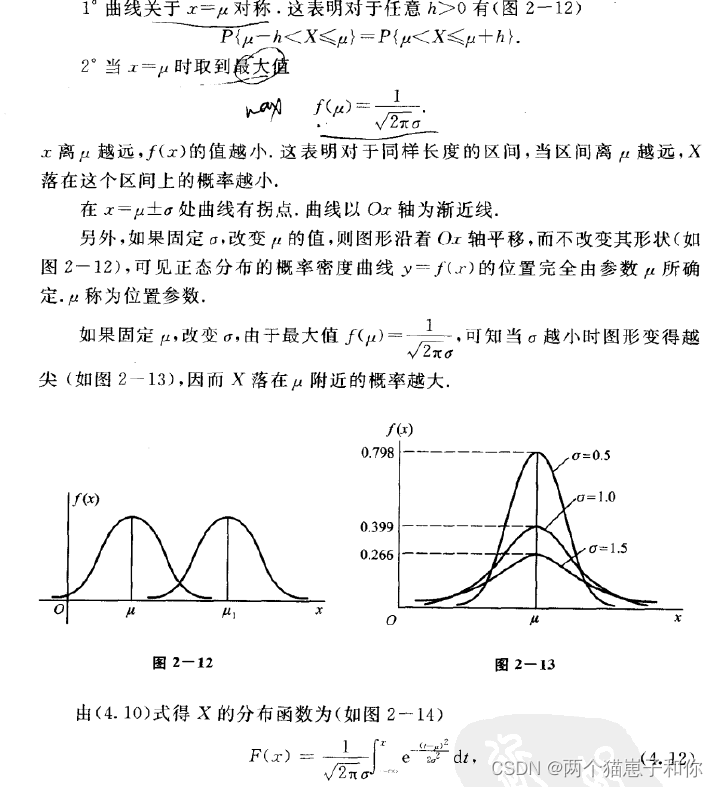
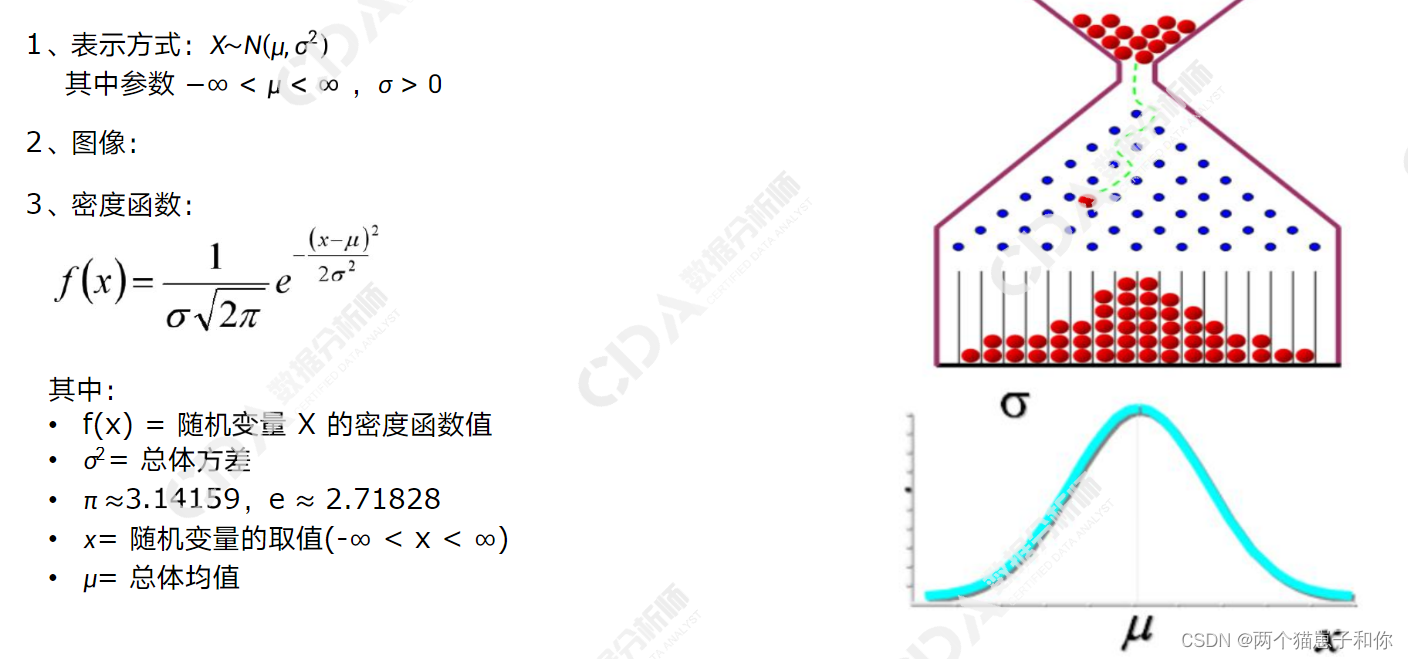
6表示将随机变量X转换为服从标准正态分布，取标准正态分布函数的函数值即可。

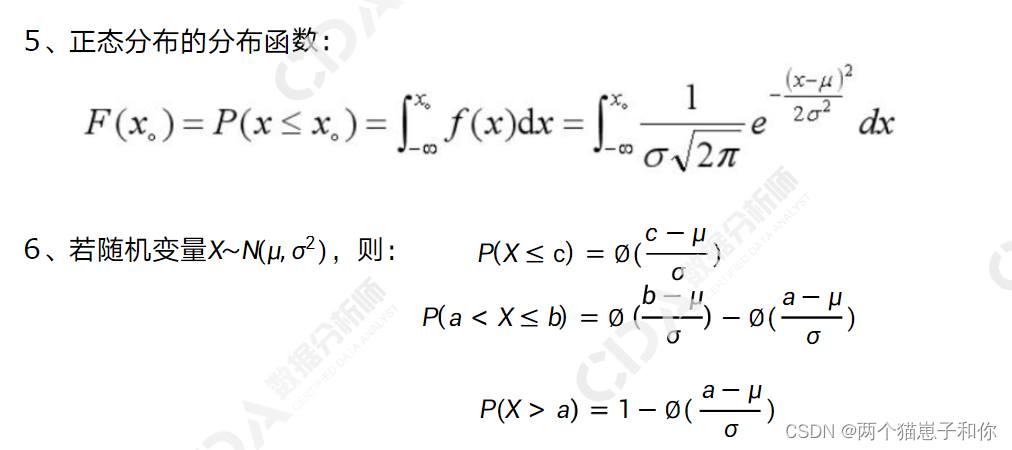
标准正态分布表

3.4.4、标准正态分布

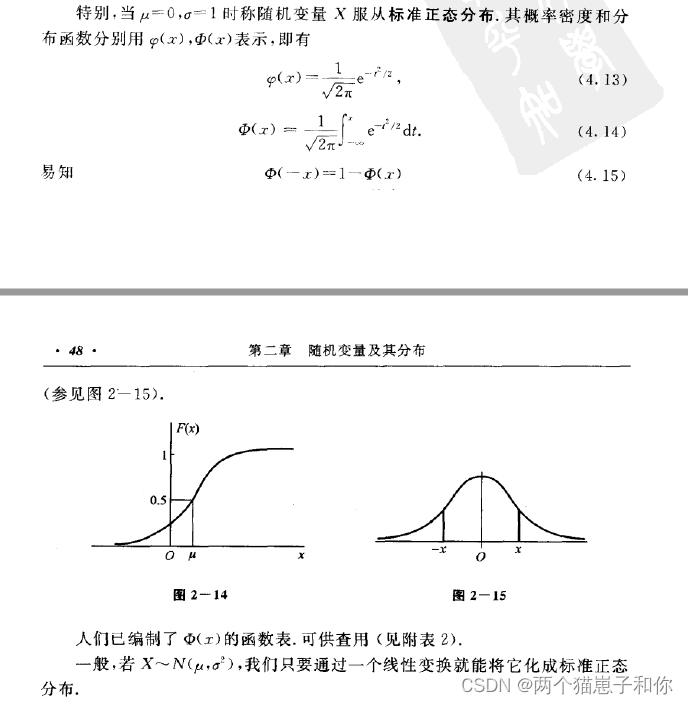
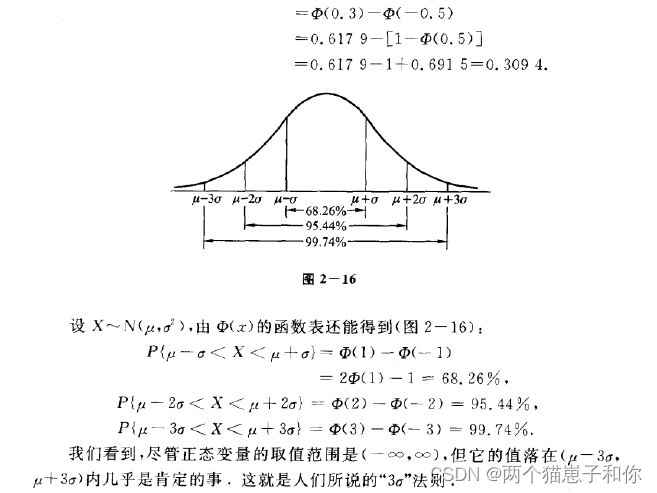
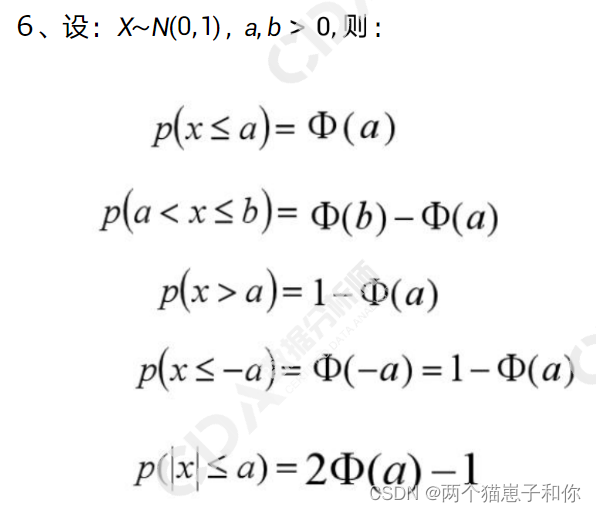
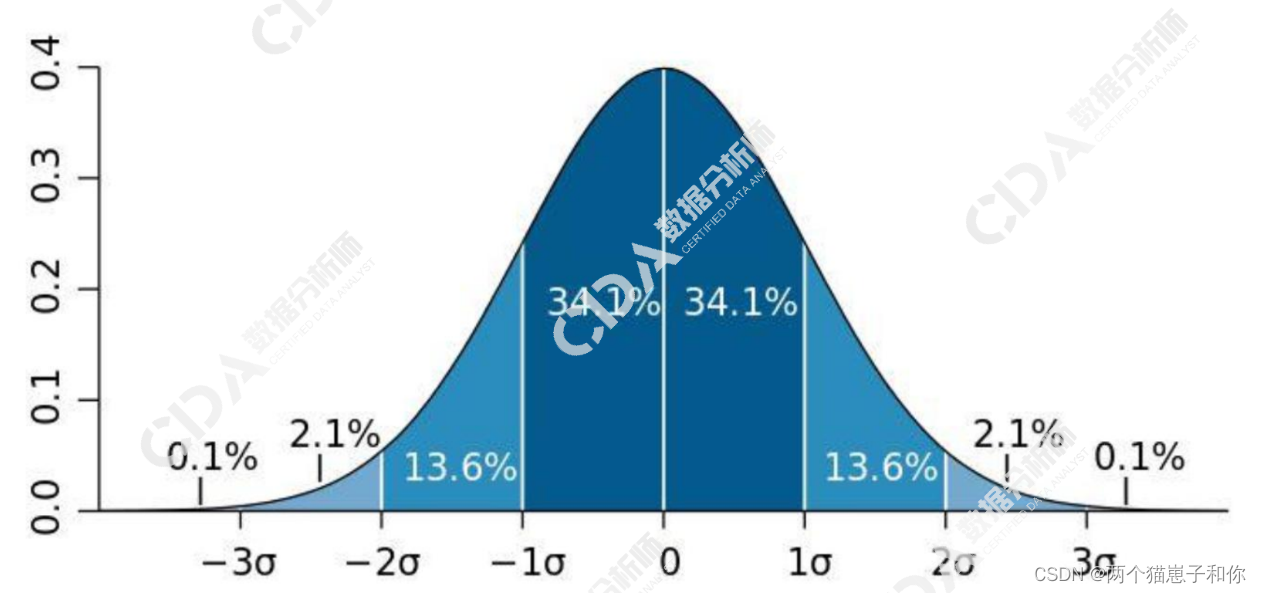
3.5、抽样分布

3.5.1、统计量

3.5.2、卡方分布（塔方分布、χ²）

3.5.1、卡方分布的定义

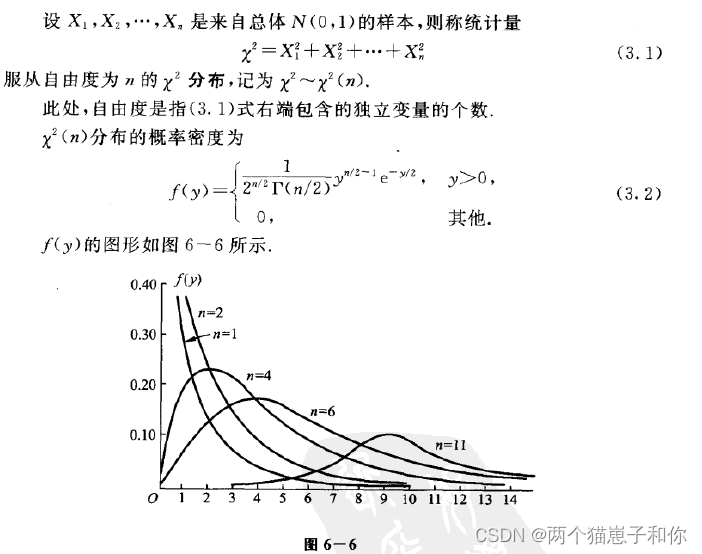
3.5.2、卡方分布的性质

3.5.3、卡方分布表

3.5.3、t分布

3.5.3.1、定义及性质

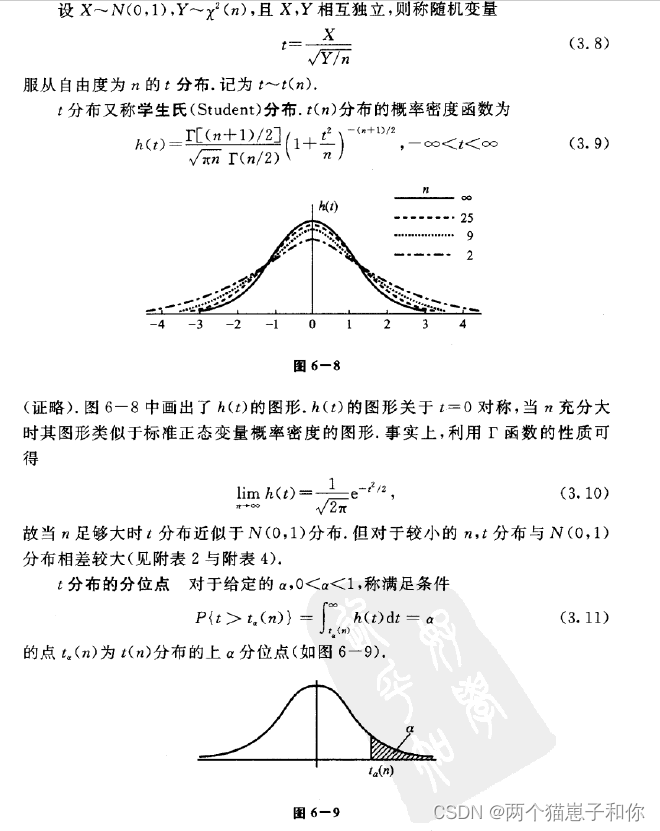
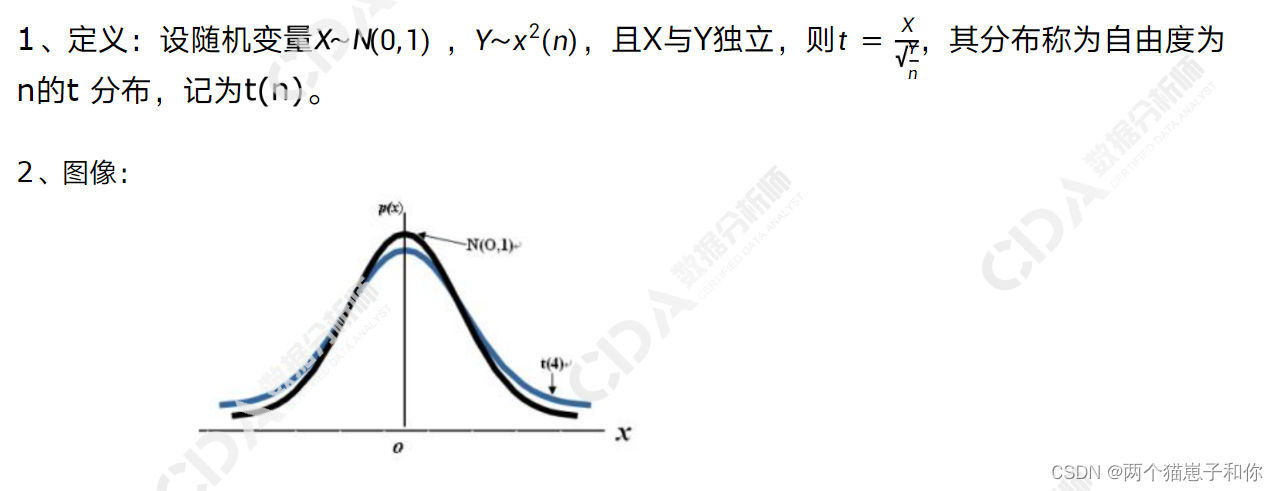
3.5.3.2、t分布表

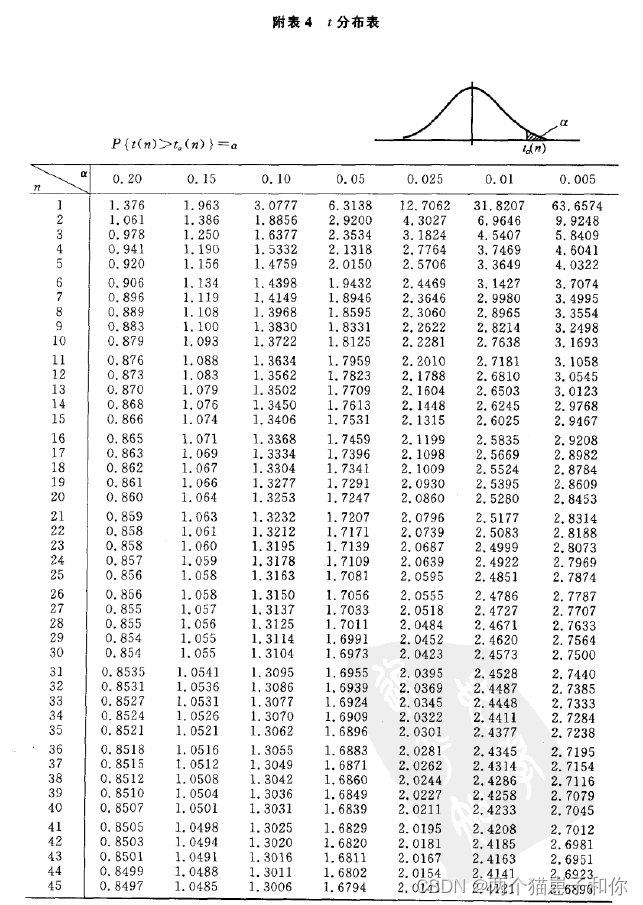
3.5.4、F分布

3.5.4.1、定义及性质

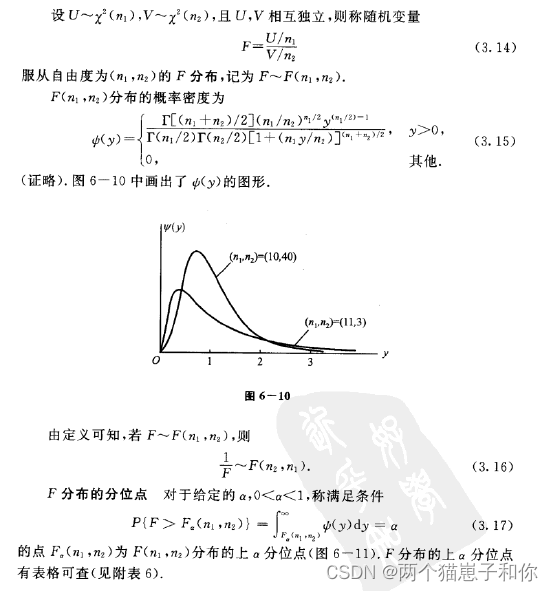
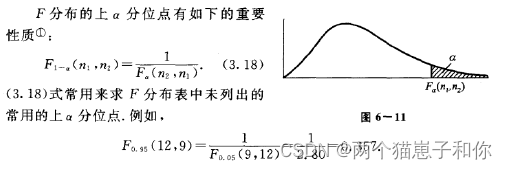
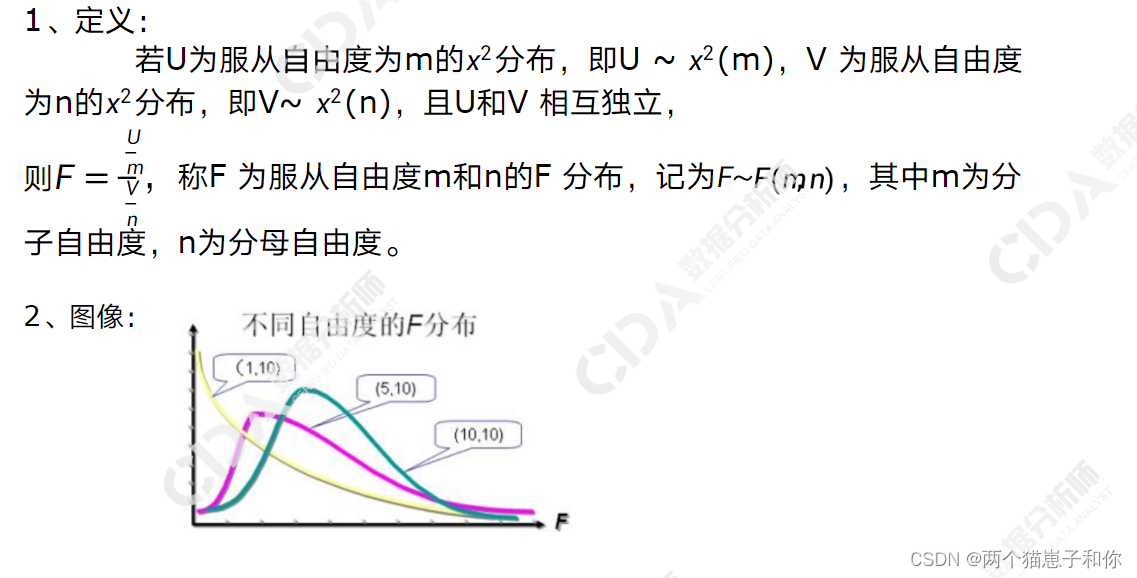
3.5.4.2、F分布表

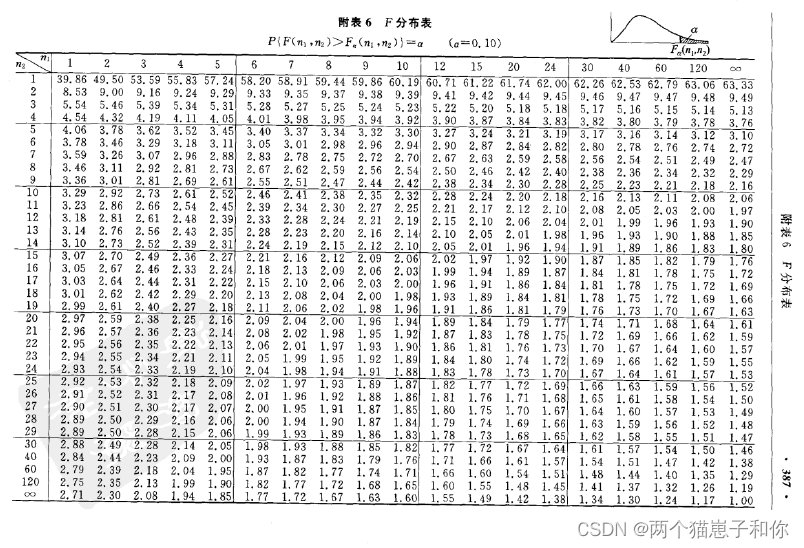
3.5.5、正态总体的样本均值与样本方差的分布