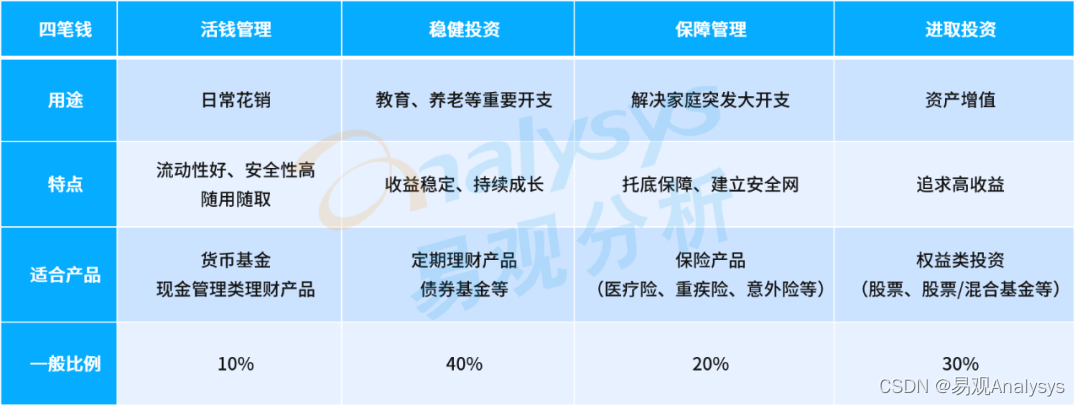
【题目描述】

n 位同学站成一排，音乐老师要请其中的 n−k 位同学出列，使得剩下的 k 位同学排成合唱队形。

合唱队形是指这样的一种队形：设 kk 位同学从左到右依次编号为 1,2, … ,k，他们的身高分别为​,​, … ,​，则他们的身高满足 <……<>……> (1≤i≤k)。  

你的任务是，已知所有 n 位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

【输入】

共二行。

第一行是一个整数 n（2≤n≤100），n 表示同学的总数。

第二行有 n 个整数，用空格分隔，第 i 个整数 ​（130≤ ​ ≤230）是第 i 位同学的身高（厘米）。

【输出】

一个整数，最少需要几位同学出列。

样例输入

8
186 186 150 200 160 130 197 220

样例输出

4

解题思路

这个题目不是单纯的递增或者递减数列，而是先递增再递减。

我首先想的是：从1 到 n 存入身高，初始化动态 dp 数组，每个里面的值赋为 i-1(例如第 1 个 dp[1]=0），然后从 2 到 n 进行遍历（代表的是递增的节制点 k），然后分情况讨论：内部进行两个循环，一个循环对 1 至 k 进行考虑，如果不满足 a[j]<a[i]，就重新赋值，dp[i]= min(dp[i],dp[j]+1),但是这里要考虑一个问题是：如果去掉了一个人（他的编号是 x），那么他的下一个人（x+1）的身高还是和第 x 个人比较，这里会有些复杂， dp 数组里面更新的最小值，是从哪一个人开始更新的，说明这个人不用考虑，可能还需要用一个值存储更新的这个人的前一个人的身高。这是计算递增情况的，然后递减情况类似。

然后我看了下题解，他们的思路都很像：是先用两层循环，目的是从第 1 个人到第 n 个人找对应下标的最大升序列，再用两层循环从第 n 个人到第 1 个人找对应下标的最大升序列。

题目不就是要找前一部分是升序，后一段是从后往前的升序嘛！那将两个升序对应的下标的值相加，注意要减一，因为前一段和后一段的中间那个数，计算了两次。

然后计算上的人数就是符合要求的，要求的是去除的人数，就用 n-max ，max是统计人数时出现的最大值。

先用代码解决找升序的问题：

for(i=1;i<=n;i++)//从左到右找递增的个数 
	{
		for(j=0;j<i;j++)
		{
			if(a[j]<a[i])
			b[i]=max(b[i],b[j]+1);
		} 
	}

不过要注意的是：尽管数列是从第 1 个人开始数的，但是内存循环的 j=0 ，全局变量中 a[0]=0,对于第一个人来说，这个人肯定要入列，这时 a[1]>a[0]，b[1]=b[0]+1（其实也可以在初始化时就把b[1]  赋值为1，也是一样的效果）。 对于后一段也是同样的思路。

代码如下：

#include<stdio.h>
int a[105];
int b[105],c[105],sum;
int max(int x,int y)
{
	if(x<y)
	return y;
	else
	return x;
}
int main()
{
	int n,i,j;
	scanf("%d",&n);
	for(i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
	}
	for(i=1;i<=n;i++)//从左到右找递增的个数 
	{
		for(j=0;j<i;j++)
		{
			if(a[j]<a[i])
			b[i]=max(b[i],b[j]+1);
		} 
	}
	for(i=n;i>0;i--)//从左往右找递减的个数 
	{
		for(j=n+1;j>i;j--)
		{
			if(a[i]>a[j])
			c[i]=max(c[i],c[j]+1);
		}
	}
	for(i=1;i<=n;i++)
	sum=max(sum,c[i]+b[i]-1);//找中途出现的最大值 
	printf("%d",n-sum);
	return 0;
}