PPOJ刷题-3

1265: 最近公共祖先

题目描述

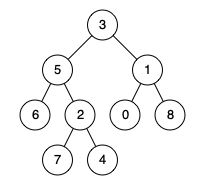
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

输入

输入两行。
第一行按照先序输入一棵二叉树，其中空节点用 -1 表示。
第二行输入两个结点的值val1, val2 , 输出该结点的双亲节点的val.(数据保证所有节点val的值都不相同)

输出

输出一行，代表最近公共祖先的val。

样例输入

3 5 6 -1 -1 2 7 -1 -1 4 -1 -1 1 0 -1 -1 8 -1 -1
5 1

样例输出

#include<bits/stdc++.h>
using namespace std;
const int N=100;
//先序遍历建立二叉树，然后对其进行先序遍历，
//如果某个结点的左子树和右子树都找到了权值为a和b的结点，则该节点就是最近公共结点
struct TreeNode {
   int val;
   TreeNode *left,*right;
};


void build(TreeNode * &T)
{
    int x;
    cin>>x;
    if(x==-1){
        T==NULL;
        return ;
    }
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);
}

TreeNode *Find(TreeNode *T,int a,int b)
{
    //如果该节点权值为a或b，或者该节点为空，返回该结点
    if(T==NULL||T->val==a||T->val==b) return T;
    //递归查找左子树和右子树，将结果分别保存在l和r
    TreeNode *l=Find(T->left,a,b),*r=Find(T->right,a,b);
    //如果在左右子树找到了，就返回该节点
    if(l && r) return T;
    //否则说明在同一子树上；对于一个结点是另一个结点祖先的情况，先找到的结点就是最近公共祖先
    else return l?l:r;
}

int main()
{
    TreeNode * T=NULL;
    build(T);
    int a,b;
    cin>>a>>b;
    cout<<Find(T,a,b)->val<<endl;
    return 0;
}

1266: 二叉树的直径

题目描述

二叉树的直径是指二叉树中相距最远的两个点的距离。如下图所示二叉树，最远的两个点是7和13或者 4和13，故二叉树直径为6.
在这里插入图片描述

输入

输入一行，按照先序输入一棵二叉树，其中空节点用 -1 表示。

输出

输出一行代表二叉树的直径。

样例输入

8 3 1 -1 -1 6 4 -1 -1 7 -1 -1 10 -1 14 13 -1 -1 -1

样例输出

#include<bits/stdc++.h>
using namespace std;
const int N=100;
//先序遍历建立二叉树，求二叉树中相距最远的两个点的距离
//只需要每个结点的的左子树的最大深度+右子树的最大深度
struct TreeNode {
   int val;
   TreeNode *left,*right;
};
int MaxL=0;

void build(TreeNode * &T)
{
    int x;
    cin>>x;
    if(x==-1){
        T==NULL;
        return ;
    }
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);
}

//求解以该节点为根节点的最大深度
int Depth(TreeNode *T,int h)
{
    //若该结点为空，就返回深度
    if(T==NULL) return h;
    //分别求出左右子树的深度
    int l=Depth(T->left,h+1),r=Depth(T->right,h+1);
    return max(l,r);
}

//寻找二叉树中相距最远的两个点的距离
void Find(TreeNode *T)
{
    if(T==NULL) return;
    int l,r;
    //左子树不为空则求左子树的深度，为空则深度为0
    l=T->left?Depth(T->left,0):0;
    //右子树不为空则求右子树的深度，为空则深度为0
    r=T->right?Depth(T->right,0):0;
    if(MaxL<l+r) MaxL=l+r;
    Find(T->left);
    Find(T->right);
}

int main()
{
    TreeNode * T=NULL;
    build(T);
    MaxL=0;
    Find(T);
    cout<<MaxL<<endl;
    return 0;
}

1364: 删除给定值的叶子节点

题目描述

PIPI有一棵二叉树和一个整数 target ，请你删除所有值为 target 的叶子节点。
注意，一旦删除值为 target 的叶子节点，它的父节点就可能变成叶子节点；如果新叶子节点的值恰好也是 target ，那么这个节点也应该被删除。
在这里插入图片描述

输入

第一行按照先序输入树T，其中空节点用 -1 表示。
第二行输入target

输出

按照先序输出删完之后的二叉树。

样例输入

1 2 2 -1 -1 -1 3 2 -1 -1 4 -1 -1
2

样例输出

1 3 4

#include<bits/stdc++.h>
using namespace std;
const int N=100;
//采用后序遍历进行查找，因为要先知道子节点被删除没有；
//记录每一个结点的父亲结点，以及当前结点是父节点的左孩子还是右孩子（0左1右）
//如果当前结点值为target并且左右子树都为空，那就将父节点的左（右）孩子置空
struct TreeNode {
   int val;
   TreeNode *left,*right;
};

void build(TreeNode * &T)
{
    int x;
    cin>>x;
    if(x==-1){
        T==NULL;
        return ;
    }
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);
}

void Delete(TreeNode *root,TreeNode *fa,int son,int target)//son=0左孩子，son=1右孩子
{
    if(!root) return;
    Delete(root->left,root,0,target);
    Delete(root->right,root,1,target);
    //如果结点值为target，且左右子树为空就删除
    if(root->val==target && root->left==NULL && root->right==NULL){
        if(son==0) fa->left=NULL;
        else fa->right=NULL;
    }
}

void Print(TreeNode *T)//先序输出
{
    if(T==NULL) return;
    printf("%d ",T->val);
    Print(T->left);
    Print(T->right);
}

int main()
{
    TreeNode * T=NULL;
    build(T);
    int target;
    cin>>target;
    Delete(T,T,-1,target);
    //根节点为target
    if(T->val==target && T->left==NULL &&T->right==NULL)
        T=NULL;
    Print(T);
    return 0;
}

1365: 祖父结点为偶数的节点

题目描述

PIPI有一棵二叉树，他想知道所有祖父结点值为偶数的结点值之和。
在这里插入图片描述

输入

输入包含一行，先序输入一棵二叉树，空节点用-1表示。

输出

输出为满足条件的结点值之和。

样例输入

6 7 2 9 -1 -1 -1 7 1 -1 -1 4 -1 -1 8 1 -1 -1 3 -1 5 -1 -1

样例输出(2+7+1+3+5=18)

#include<bits/stdc++.h>
using namespace std;
const int N=100;
//每次遍历保存该节点的父节点和祖父结点，判断祖父结点是否为偶数即可
//递归时，当前结点变父节点，父节点变祖父结点
struct TreeNode {
   int val;
   TreeNode *left,*right;
};
int ans=0;//统计数值之和

void build(TreeNode * &T)
{
    int x;
    cin>>x;
    if(x==-1){
        T==NULL;
        return ;
    }
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);
}

void DFS(TreeNode *T,TreeNode *fa,TreeNode *gfa)//进行中序遍历
{
    if(!T) return;
    DFS(T->left,T,fa);
    //祖父结点存在且为偶数
    if(gfa&&gfa->val%2==0) ans+=T->val;
    DFS(T->right,T,fa);
}

int main()
{
    TreeNode * T=NULL;
    build(T);
    DFS(T,NULL,NULL);
    cout<<ans<<endl;
    return 0;
}

1369: 二叉树的最大深度

题目描述

给定一个二叉树，找出其最大深度。
最大深度是从根节点到最远叶子节点的最长路径上的节点数量。

输入

输入一行，按照先序输入一棵二叉树，其中空节点用 -1 表示。

输出

输出一行代表二叉树的最大深度。

样例输入

1 2 -1 -1 3 4 -1 -1 -1

样例输出

#include<bits/stdc++.h>
using namespace std;
const int N=100;

struct TreeNode {
   int val;
   TreeNode *left,*right;
};

void build(TreeNode * &T)
{
    int x;
    cin>>x;
    if(x==-1){
        T==NULL;
        return ;
    }
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);
}

int Height(TreeNode *T,int h)
{
    if(T==NULL) return h;
    return max(Height(T->left,h+1),Height(T->right,h+1));
}

int main()
{
    TreeNode * T=NULL;
    build(T);
    cout<<Height(T,0)<<endl;
    return 0;
}

1370: 高度平衡的二叉树

题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。
一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。

输入

输入一行，按照先序输入一棵二叉树，其中空节点用 -1 表示。

输出

若是则输出YES，否则输出NO。

样例输入

1 2 -1 -1 3 4 -1 -1 -1

样例输出

YES

#include<bits/stdc++.h>
using namespace std;
const int N=100;
//用flag标记二叉树是否平衡，对每个结点计算两个子树的高度差
struct TreeNode {
   int val;
   TreeNode *left,*right;
};
int flag=1;
void build(TreeNode * &T)
{
    int x;
    cin>>x;
    if(x==-1){
        T==NULL;
        return ;
    }
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);
}

int Height(TreeNode *T,int h)
{
    if(T==NULL) return h;
    return max(Height(T->left,h+1),Height(T->right,h+1));
}

void Judge(TreeNode *T)
{
    if(!flag||T==NULL) return;
    if(abs(Height(T->left,0)-Height(T->right,0))>1) flag=0;
    //继续递归判断左右子树
    Judge(T->left);
    Judge(T->right);
}

int main()
{
    TreeNode * T=NULL;
    build(T);
    Judge(T);
    if(flag)
        printf("YES\n");
    else
        printf("NO\n");
    return 0;
}

1371: 求根到叶子结点数字之和

题目描述

给定一个二叉树，它的每个结点都存放一个1-9的数字，每条从根到叶子节点的路径都代表一个数字。
例如，从根到叶子节点路径 1->2->3 代表数字 123。
计算从根到叶子节点生成的所有数字之和，答案保证在int范围。

输入

输入一行，按照先序输入一棵二叉树，其中空节点用 -1 表示。

输出

输出根到叶子节点生成的所有数字之和。

样例输入

1 2 -1 -1 3 4 -1 -1 -1

样例输出

#include<bits/stdc++.h>
using namespace std;
const int N=100;
//用变量sum来统计所有数字之和，每次递归到了根节点，就把数字加到sum中，然后结束递归
struct TreeNode {
   int val;
   TreeNode *left,*right;
};
int sum=0;
void build(TreeNode * &T)
{
    int x;
    cin>>x;
    if(x==-1){
        T==NULL;
        return ;
    }
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);
}

void Plus(TreeNode *T,int ans)
{
    //如果为叶子结点，结束递归
    if(T->left==NULL&&T->right==NULL) sum+=ans*10+T->val;
    //否则继续在左右子树递归查找叶子结点
    if(T->left!=NULL) Plus(T->left,ans*10+T->val);
    if(T->right!=NULL) Plus(T->right,ans*10+T->val);
}

int main()
{
    TreeNode * T=NULL;
    build(T);
    Plus(T,0);
    cout<<sum<<endl;
    return 0;
}

1372: 找树左下角的值

题目描述

给定一个二叉树，在树的最后一行找到最左边的值。

输入

输入一行，按照先序输入一棵二叉树，其中空节点用 -1 表示。

输出

输出树的最后一行最左边的值。

样例输入

1 2 -1 -1 3 4 -1 -1 -1

样例输出

#include<bits/stdc++.h>
using namespace std;
//按照先序遍历遍历整棵树，保存深度最深的第一个遍历到的叶子结点的值
const int N=100;
struct TreeNode {
   int val;
   TreeNode *left,*right;
};
int H=0,x;
void build(TreeNode * &T)
{
    int x;
    cin>>x;
    if(x==-1){
        T==NULL;
        return ;
    }
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);
}

void findk(TreeNode *T,int h)
{
    //如果是叶子结点
    if(T->left==NULL&&T->right==NULL){
        //深度比之前的深度大，更新H和x
        if(H<h)
            H=h,x=T->val;
        return;
    }
    if(T->left!=NULL)
        findk(T->left,h+1);
    if(T->right!=NULL)
        findk(T->right,h+1);
}

int main()
{
    TreeNode * T=NULL;
    build(T);
    findk(T,1);
    cout<<x<<endl;
    return 0;
}

1373: 在每个树行中找最大值

题目描述

在二叉树的每一行中找到最大的值。

输入

输入一行，按照先序输入一棵二叉树，其中空节点用 -1 表示。

输出

从根节点开始往下输出树的每一行的最大值。

样例输入

1 2 -1 -1 3 4 -1 -1 -1

样例输出

1 3 4

#include<bits/stdc++.h>
using namespace std;
//按照先序遍历遍历整棵树，遍历中更新树的最大深度，同时记录每层的最大值
const int N=100;
struct TreeNode {
   int val;
   TreeNode *left,*right;
};
int H=0,x;
int ans[100];//存储每层的最大值
void build(TreeNode * &T)
{
    int x;
    cin>>x;
    if(x==-1){
        T==NULL;
        return ;
    }
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);
}

void findk(TreeNode *T,int h)
{
    //如果是叶子结点
    if(T==NULL) return;
    if(T->val>ans[h]) ans[h]=T->val;
    if(H<h) H=h;
    findk(T->left,h+1);
    findk(T->right,h+1);
}

int main()
{
    TreeNode * T=NULL;
    build(T);
    findk(T,1);
    for(int i=1;i<=H;i++)
        printf("%d ",ans[i]);
    return 0;
}

1374: 层数最深叶子节点的和

题目描述

给你一棵二叉树，请你返回层数最深的叶子节点的和。

输入

输入一行，按照先序输入一棵二叉树，其中空节点用 -1 表示。

输出

输出层数最深的叶子节点的和。

样例输入

1 2 -1 -1 3 4 -1 -1 -1

样例输出

#include<bits/stdc++.h>
using namespace std;
//按照先序遍历遍历整棵树，遍历中更新树的最大深度，进行遍历累加最大深度的结点值
const int N=100;
struct TreeNode {
   int val;
   TreeNode *left,*right;
};
int H,sum=0;
void build(TreeNode * &T)
{
    int x;
    cin>>x;
    if(x==-1){
        T==NULL;
        return ;
    }
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);
}

int Height(TreeNode *T,int h)
{
    if(T==NULL) return h;
    return max(Height(T->left,h+1),Height(T->right,h+1));
}

void findk(TreeNode *T,int h)
{
    //如果是叶子结点
    if(T==NULL) return;
    if(h==H) sum+=T->val;
    findk(T->left,h+1);
    findk(T->right,h+1);
}

int main()
{
    TreeNode * T=NULL;
    build(T);
    H=Height(T,0);
    findk(T,1);
    cout<<sum<<endl;
    return 0;
}

1099: PIPI的油田(DFS遍历次数)

题目描述

PIPI承包了一大片土地，PIPI打了几个油井，发现这片土地的下面有很多地方埋藏着石油，如果一个油井与另一个油井在上，下，左，右，左上，右下，右上，左下这八个方向中的任意一个方向连通，我们就认为这两个油井属于同一个油田。
现在这块土地可以看成是一个nm的方格矩阵，标记为’@‘的方格代表一个油井，标记为’'的方格代表一块贫瘠的土地。你能告诉PIPI他的这块土地上有几个油田吗?

输入

输入包含多组测试样例。
对于每组测试样例，输入的第一行是两个正整数 n,m (1<=n,m<=100)
接下来输入的一个n*m的方格矩阵，代表PIPI承包土地。
以 0 0结尾结束输入。

输出

对于每组测试样例，输出一行，代表土地上油田的数目。

样例输入

1 1
*
3 5
*@*@*
**@**
*@*@*
1 8
@@****@*
5 5 
****@
*@@*@
*@**@
@@@*@
@@**@
0 0

样例输出

#include<bits/stdc++.h>
using namespace std;
const int N=105;
char mp[N][N];
int n,m;
int dir[8][2]={{1,0},{0,1},{-1,0},{0,-1},{-1,-1},{-1,1},{1,-1},{1,1}};

void DFS(int x,int y)
{
    mp[x][y]='*';
    for(int i=0;i<8;i++){
        int nextx=x+dir[i][0];
        int nexty=y+dir[i][1];
        if(nextx>=1&&nextx<=n&&nexty>=1&&nexty<=m&&mp[nextx][nexty]=='@')
            DFS(nextx,nexty);
    }
}

int main()
{
    while(cin>>n>>m&&n&&m){
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
              cin>>mp[i][j];
        int cnt=0;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                if(mp[i][j]=='@'){
                    cnt++;
                    DFS(i,j);
                }
            }
        }
        cout<<cnt<<endl;
    }
    return 0;
}

1400: 八大排序——直接插入排序

题目描述

请使用直接插入排序算法对题中给出的数据进行排序。
PS：你也可以使用二分优化的插入排序。

输入

输入的第一行包含1个正整数n，表示共有n个整数需要参与排序。其中n不超过1000。

第二行包含n个用空格隔开的正整数，表示n个需要排序的整数。

输出

只有1行，包含n个整数，表示从小到大排序完毕的所有整数。

请在每个整数后输出一个空格。

样例输入

10
2 8 4 6 1 10 7 3 5 9

样例输出

1 2 3 4 5 6 7 8 9 10

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int a[N];
//直接插入排序的基本操作是将一个记录插入到已经排好序的有序表中
//从而得到一个新的且记录数增加1的有序表
//a[0]作为哨兵，作用：1 暂时存放待插入的元素；2 防止数组下标越界
void InsertSort(int a[],int n)
{
    int i,j;
    for(i=2;i<=n;i++){
        a[0]=a[i];
        for(j=i-1;a[j]>a[0];j--){//寻找插入位置，并将元素后移挪出位置
            a[j+1]=a[j];
        }
        a[j+1]=a[0];//将元素插入合适的位置
    }
}

int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    InsertSort(a,n);
    for(int i=1;i<=n;i++)
        printf("%d ",a[i]);
    return 0;
}

1401: 八大排序——希尔排序

题目描述

请使用希尔排序算法对题中给出的数据进行排序。

输入

输入的第一行包含1个正整数n，表示共有n个整数需要参与排序。其中n不超过1000。
第二行包含n个用空格隔开的正整数，表示n个需要排序的整数。

输出

只有1行，包含n个整数，表示从小到大排序完毕的所有整数。
请在每个整数后输出一个空格，并请注意行尾输出换行。

样例输入

10
2 8 4 6 1 10 7 3 5 9

样例输出

1 2 3 4 5 6 7 8 9 10

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int a[N];
//直接插入排序的基本操作是将一个记录插入到已经排好序的有序表中
//从而得到一个新的且记录数增加1的有序表
//a[0]作为哨兵，作用：1 暂时存放待插入的元素；2 防止数组下标越界
//希尔排序是插入排序的一种高效率实现，也叫缩小增量排序
//基本思想：先将整个待排记录分割称为若干个子序列进行直接插入排序
//带整个序列基本有序时再对全体记录进行一次直接插入排序
void Shell_Insert(int a[],int n,int d)//步长为d的插入排序
{
    int i,j;
    for(i=d+1;i<=n;i+=d){
        a[0]=a[i];
        for(j=i-d;a[j]>a[0];j-=d){//把普通插入排序当成d=1来理解
            a[j+d]=a[j];
        }
        a[j+d]=a[0];//将元素插入合适的位置
    }
}

void ShellSort(int a[],int n)
{
    int d=n/2;//初始步长为表长一半
    while(d>=1){//步长大于等于1时继续执行
        Shell_Insert(a,n,d);
        d/=2;
    }
}

int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    ShellSort(a,n);
    for(int i=1;i<=n;i++)
        printf("%d ",a[i]);
    return 0;
}

1406: 八大排序——归并排序

题目描述

请使用归并排序对题中给出的数据进行排序。

输入

输入的第一行包含1个正整数n，表示共有n个整数需要参与排序。其中n不超过100000。
第二行包含n个用空格隔开的正整数，表示n个需要排序的整数。

输出

只有1行，包含n个整数，表示从小到大排序完毕的所有整数。
请在每个整数后输出一个空格，并请注意行尾输出换行。

样例输入

10
2 8 4 6 1 10 7 3 5 9

样例输出

1 2 3 4 5 6 7 8 9 10

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int a[N],tmp[N];
//将两个或以上的有序表合并成为一个新的有序表
//常见的时2-路归并排序

void Merge(int a[],int l,int mid,int r)
{
    //使用辅助数组 tmp 将a数组[l,mid]与[mid+1,r]两端区间合并
    int i=l,j=mid+1,k=0;
    while(i<=mid&&j<=r){
        if(a[i]<=a[j]) tmp[k++]=a[i++];
        else tmp[k++]=a[j++];
    }
    while(i<=mid) tmp[k++]=a[i++];
    while(j<=r) tmp[k++]=a[j++];
    for(i=l,j=0;i<=r;i++,j++)//从tmp数组返回a数组
        a[i]=tmp[j];
}

void MergeSort(int a[],int l,int r)
{
    if(l>=r) return;
    int mid=(l+r)/2;
    MergeSort(a,l,mid);
    MergeSort(a,mid+1,r);
    Merge(a,l,mid,r);
}

int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    MergeSort(a,1,n);
    for(int i=1;i<=n;i++)
        printf("%d ",a[i]);
    return 0;
}

1402: 八大排序——简单选择排序

题目描述

请使用简单选择排序算法对题中给出的数据进行排序。

输入

输入的第一行包含1个正整数n，表示共有n个整数需要参与排序。其中n不超过1000。
第二行包含n个用空格隔开的正整数，表示n个需要排序的整数。

输出

只有1行，包含n个整数，表示从小到大排序完毕的所有整数。
请在每个整数后输出一个空格，并请注意行尾输出换行。

样例输入

10
2 8 4 6 1 10 7 3 5 9

样例输出

1 2 3 4 5 6 7 8 9 10

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int a[N];
//每趟排序中确定一个第i大的值

void SelectSort(int a[],int n)
{
    for(int i=1;i<n;i++){
        int Minid=i;//初始化最小下标为i
        for(int j=i+1;j<=n;j++){
            if(a[j]<a[Minid]){
                Minid=j;
            }
        }
        swap(a[Minid],a[i]);//交换位置
    }
}

int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    SelectSort(a,n);
    for(int i=1;i<=n;i++)
        printf("%d ",a[i]);
    return 0;
}

1404: 八大排序——冒泡排序

题目描述

请使用冒泡排序对题中给出的数据进行排序。

输入

输入的第一行包含1个正整数n，表示共有n个整数需要参与排序。其中n不超过1000。
第二行包含n个用空格隔开的正整数，表示n个需要排序的整数。

输出

只有1行，包含n个整数，表示从小到大排序完毕的所有整数。
请在每个整数后输出一个空格，并请注意行尾输出换行。

样例输入

10
2 8 4 6 1 10 7 3 5 9

样例输出

1 2 3 4 5 6 7 8 9 10

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int a[N],flag;
//比较相邻元素，如果第一个比第二个大，交换位置
//用flag来标记，如果一趟排序中没有交换位置就已经有序

void BubbleSort(int a[],int n)
{
    for(int i=0;i<n-1;i++){//进行n-1趟排序
        flag=0;
        for(int j=1;j<n-i;j++){
            if(a[j]>a[j+1]){
                flag=1;
                swap(a[j],a[j+1]);
            }
        }
        if(flag==0)//未交换过位置已经有序
            return;
    }
}

int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    BubbleSort(a,n);
    for(int i=1;i<=n;i++)
        printf("%d ",a[i]);
    return 0;
}

1203: PIPI发工资(拓扑排序)

题目描述

PIPI开了一个工厂，工厂里面有许许多多的员工。每次要发工资的时候PIPI就开始思考了，如何才能给员工发最少的工资呢?
发工资的原则是这样的: 每个员工的工资都是一个整数，其中基本工资是888元，但是如果 A 是 B的上司，那么A的工资就要比B高。
现在给出员工的数量和员工之间的关系，PIPI想问下胖虎他最少要发多少钱？？

输入

输入包含多组测试用例。
对于每一组测试用例，第一行包含两个整数 n (n<=10000)和 m (m<=20000)。表示PIPI工厂里面员工数量以及员工之间的关系数目。
接下来m行每一行包含两个整数 a和 b 。代表 a 是 b的的上司(1<=a,b<=n)。

输出

对于每组测试用例，输出PIPI最少需要发多少工资。如果PIPI没办法发工资，输出-1。

样例输入

样例输出

1777
-1

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+5;
//利用拓扑排序进行查找，看是否有环，如果有选说明没法发工资
//拓扑排序过程中按照入度为0进行入队，然后进行工资的调整
//此题不好用并查集进行解决，因为并查集只能处理无向环；有向环的处理有拓扑飘絮和DFS

struct edge{
   int to,next;
}e[2*N];
int cnt;
int indegree[N];
int salary[N];
int head[N];

void Add(int u,int v)//构建有向边
{
    e[cnt].to=v;
    e[cnt].next=head[u];
    head[u]=cnt++;
}

int main()
{
    int n,m;
    while(cin>>n>>m){
        cnt=1;
        int sum=0,ans=0;//工资总额，统计结点个数
        queue<int> q;
        for(int i=1;i<=n;i++){//初始化数组
            indegree[i]=0;
            salary[i]=0;
            head[i]=-1;
        }
        for(int i=0;i<m;i++){
            int a,b;
            cin>>a>>b;
            Add(b,a);//创建边
            indegree[a]++;
        }
        for(int i=1;i<=n;i++)
            if(!indegree[i])
              q.push(i);
        while(!q.empty()){
            int u=q.front();
            q.pop();
            ans++;
            for(int i=head[u];i!=-1;i=e[i].next)//将与u相邻的点入度-1
            {
                int v=e[i].to;
                salary[v]=salary[v]>salary[u]+1?salary[v]:salary[u]+1;
                indegree[v]--;
                if(indegree[v]==0)
                    q.push(v);
            }
        }
        if(ans<n)
            printf("-1\n");
        else{
            for(int i=1;i<=n;i++)
                sum+=salary[i];
            sum+=888*n;
            printf("%d\n",sum);
        }
    }
    return 0;
}

1545: 哈夫曼树（求带权路径长度）

题目描述

有一棵二叉树有n个叶子结点，每个叶子结点有一个权值，求最小带权路径长度。

输入

多组输入。
第一行输入叶子结点数n（1<=n<=1000）。
接下来一行输入n个正整数（不超过1000），代表每个叶子结点的权值。

输出

输出由这n个叶子结点构成的二叉树的最小带权路径长度。

样例输入

3
1 2 3

样例输出

提示

对于测试用例，可以构建一棵这样的树：
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
//通常我们计算哈夫曼树的带权路径长度，可以通过每次取点集中最小的两个结点构建一个新节点
//构建完后，在取叶子结点值*深度-1，累加可得最小带权路径长度
//但是这样太过于麻烦，可以先将叶子结点放入优先队列，每次取出最小两个，相加后放入队列中，把相加的
//值用变量sum存储起来，直至队列为空即可

int main()
{
    int n;
    while(cin>>n){
        priority_queue<int,vector<int>,greater<int> > p;//建立从小到大的优先队列，默认是从大到小
        //默认是:priority_queue<int> p;
        for(int i=0;i<n;i++){
            int x;
            cin>>x;
            p.push(x);
        }
        int sum=0;
        while(p.size()!=1){//出队结点直达只剩一个结点，说明哈夫曼树构建完成
            int a=p.top();//取出最小值
            p.pop();
            int b=p.top();//取出次小值
            p.pop();
            sum+=a+b;
            p.push(a+b);//将新的结点放入
        }
        cout<<sum<<endl;
    }
    return 0;
}

1382: PIPI染色（二分图判断，染色法）

题目描述

PIPI有一个n个顶点m条边的连通无向图，节点编号为1~n，现在它想对这个图进行染色，要求相邻的顶点颜色不同。它想知道是否能最多用2种颜色进行染色？
题目保证没有重边和自环。
以下内容更新于2021/5/14
该题在21年943初试被出在了真题压轴题中，题面如下:
给定图G=(V,E)，如果点集V能够被分为两个不相交子集V1和V2，使得V1∪V2=V，且V1中的任何两个结点在图G中没有边，V2中的任何两个结点在图G中也没有边，则称图G为一个二部图。对于任意给定的图G，设计算法判断图G是否是一个二部图，并给出时间复杂度。

输入

第一行两个整数n,m(1<=n<=1000),数据保证没有重边和自环。
接下来m行，每行两个整数，表示这条边连接的两个顶点。

输出

如果可以用最多两种颜色进行染色，输出YES,否则输出NO

样例输入

样例输出

NO

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
vector<int> mp[N];  //动态数组存储图的邻接表
int color[N];    //自定义颜色数组，表示结点的颜色
int flag=1;     //标记位，如果是二分图则置1，否则置为0

void DFS(int x){ //邻接表性质，利用深搜进行结点染色
   if(flag==0) return ;//不能够进行染色
   for(int i=0;i<mp[x].size();i++){
       int next=mp[x][i];  //当前结点的下一个结点
       if(!color[next]) color[next]=color[x]*-1,DFS(next);// 如果下一个顶点没有被染色，就将其染成相反的颜色 其中 1 表示一种颜色 -1表示另一种颜色
       else if(color[next]&&color[x]==color[next])//下一个顶点与当前顶点染色相同
        flag=0;
   }
}

int main()
{
    int n,m;
    cin>>n>>m;
    while(m--){
        int u,v;
        cin>>u>>v;
        mp[u].push_back(v);//因为是无向图，所以加两条边
        mp[v].push_back(u);
    }
    color[1]=1;//对第一个顶点染色
    for(int i=1;i<=n;i++){
        DFS(i);
    }
    if(flag) printf("YES\n");
    else printf("NO\n");
    return 0;
}

1447: PIPI的线性表问题Ⅰ

题目描述

已知线性表中的元素以递增序列排列，并以单链表作存储结构。设计算法删除表中所有值相同的多余元素（使得操作后的线性表中所有的值均不相同），同时释放被删结点空间，并分析算法的时间复杂度。

输入

第一行输入一个正整数n，表示元素个数，n<=100。
第二行输入n个正整数元素，保证元素以递增排列，元素的值<=100。

输出

输出删除相同元素后的链表。

样例输入

5
1 1 3 4 4

样例输出

1 3 4

#include<bits/stdc++.h>
using namespace std;
typedef struct LNode{//typedef用于将LNode改别名LinkList指针类型，可以创建指针，不用再添加'*'
   int data;
   LNode *next;
}*LinkList,LNode;

void Print(LinkList L){
   LNode *p=L->next;
   while(p){
      printf("%d ",p->data);
      p=p->next;
   }
}

void CreateList(LinkList &L,int len)
{
    L=new LNode();
    L->next=NULL;
    LNode *p=L;
    while(len--){
        p->next=new LNode();
        p=p->next;
        p->next=NULL;
        cin>>p->data;
    }
}

void DelDouble(LNode *flag)
{
    //到最后一个节点停止删除操作
    if(flag->next==NULL){
        return;
    }
    LNode *p=flag,*q=flag->next,*del=NULL;
    while(q){
        if(q->data==flag->data){
            del=q;//要删除的节点
            q=q->next;
            p->next=q;//链接后面的节点
            delete del;
        }else{
            p=p->next;
            q=q->next;
        }
    }
}

int main()
{
    int n;
    cin>>n;
    LinkList L;
    CreateList(L,n);
    LNode *flag=L->next;//头结点的下一个节点
    while(flag){
        //删除重复节点
        DelDouble(flag);
        flag=flag->next;
    }
    Print(L);
    return 0;
}

中序遍历+层次遍历还原二叉树

#include<bits/stdc++.h>
using namespace std;
//由层次遍历和中序遍历也能够还原二叉树，二叉树的每个子树的根节点总是先于子树访问
//所以可以在中序遍历找到该根节点，然后将子树分成两部分，左子树和右子树，然后继续递归构建
//二叉树，知道中序遍历的起点大于终点，即表示构建树结束
typedef struct TNode
{
    char val;
    TNode *left,*right;
};
char level[10]={'A','B','C','D','E','F','G','H','I'};
char in[10]={'D','B','E','A','H','F','I','C','G'};

TNode* CreateTree(int l1,int r1,int l2,int r2){
    if(l2>r2)//遍历结束
        return NULL;
    //printf("%d %d %d %d\n",l1,r1,l2,r2);
    TNode* bt=new TNode();
    int i,j;//分别指向层次遍历level和中序遍历in中的元素
    int flag=0;//判定是否找到根节点
    //二层循环寻找根节点，因为不是第一个就一定是根节点
    for(i=l1;i<=r1;i++){
        for(j=l2;j<=r2;j++){
            if(level[i]==in[j]){
                flag=1;
                break;
            }
        }
        if(flag) break;
    }
    bt->val=level[i];//或者in[j]
    //printf("%d %c\n",j,bt->val);
    bt->left=CreateTree(l1+1,r1,l2,j-1);//注意递归时是中序遍历的j
    bt->right=CreateTree(l1+1,r1,j+1,r2);
    return bt;
}

void PreOrder(TNode *T)//先序遍历
{
    if(T==NULL) return;
    printf("%c",T->val);
    PreOrder(T->left);
    PreOrder(T->right);
}

void InOrder(TNode* T)//中序遍历
{
    if(T==NULL) return;
    InOrder(T->left);
    printf("%c",T->val);
    InOrder(T->right);
}

int main()
{
    int len=strlen(level);
    cout<<len<<endl;
    cout<<level[1]<<endl;
    TNode *root=CreateTree(0,len-1,0,len-1);
    PreOrder(root);
    printf("\n");
    InOrder(root);
    return 0;
}

关键路径

输入

输出

ve数组：0 6 4 5 7 7 16 14 18
vl数组：0 6 6 8 7 10 16 14 18
关键路径：1 2 5 7 8 9

代码

#include<bits/stdc++.h>
using namespace std;
#define N 20
//求解步骤
// 1、从源点V1出发，令ve[1]=0，利用拓扑排序求各个顶点（事件）的最早开始时间ve
// 2、从汇点Vn出发，令vl[n]=ve[n]，利用逆拓扑排序求各个顶点（事件）的最晚开始时间vl
// 3、根据各顶点的ve和vl，计算每条弧（活动）的e[i]和l[i]，找出e[i]==l[i]的活动即为关键活动
// 简单点说：拓扑排序取最大值求出ve[i],逆拓扑排序取最小值求出vl[i],最后找出ve[i]==vl[i]的顶点，
// 即为关键路径上的顶点，将这些顶点连接起来就是关键路径

int mp[N][N];//邻接矩阵
int V,E;//顶点数和边数
int ID[N],OD[N];//存储各顶点的入度和出度，入度用于拓扑排序，出度用于逆拓扑排序
int ve[N],vl[N];//事件最早开始时间和事件最晚开始时间；拓扑排序ve取最大，逆拓扑排序vl取最小


int main()
{
    memset(mp,-1,sizeof(mp));
    int a,b,v;//表示a->b的权值为v的有向边
    //输入顶点数
    cin>>V;
    //输入边数
    cin>>E;
    for(int i=0;i<E;i++){
        cin>>a>>b>>v;
        mp[a][b]=v;
    }
    //初始化ve为0
    memset(ve,0,sizeof(ve));

    //统计各顶点入度
    for(int i=1;i<=V;i++){
        int k=0;//用于计算入度
        for(int j=1;j<=V;j++){
            if(mp[j][i]!=-1)//如果顶点i->j有边，顶点i的入度+1
                k++;
        }
        ID[i]=k;
    }
    //拓扑排序
    for(int i=1;i<=V;i++){
        if(ID[i]==0){
            for(int j=1;j<=V;j++){
                if(mp[i][j]!=-1){//如果存在i->j,则删除这条边，并且j的入度-1
                    if(ve[j]<ve[i]+mp[i][j])
                       ve[j]=ve[i]+mp[i][j];
                    ID[j]--;
                }
            }
        }
    }

    //统计各顶点出度
    for(int i=1;i<=V;i++){
        int k=0;//用于计算出度
        for(int j=1;j<=V;j++){
            if(mp[i][j]!=-1)
                k++;
        }
        OD[i]=k;
    }
    //将vl的值全部初始化为 ve[n]（汇点的最早开始时间）
    for(int i=1;i<=V;i++)
        vl[i]=ve[V];
    //逆拓扑排序 从汇点开始，从后往前开始找
    for(int i=V;i>=1;i--){
        if(OD[i]==0){//顶点出度为0
            for(int j=1;j<=V;j++){
                if(mp[j][i]!=-1){//存在j->i的边
                    if(vl[j]>vl[i]-mp[j][i])//更新最迟开始时间,取最小值
                        vl[j]=vl[i]-mp[j][i];
                    OD[j]--;
                    //cout<<j<<' '<<i<<' '<<vl[i]<<' '<<vl[j]<<endl;
                }
            }
        }
    }
    printf("ve数组：");
    for(int i=1;i<=V;i++)
        printf("%d ",ve[i]);
    printf("\nvl数组：");
    for(int i=1;i<=V;i++)
        printf("%d ",vl[i]);
    printf("\n关键路径：");
    for(int i=1;i<=V;i++){
        if(ve[i]==vl[i])
            printf("%d ",i);
    }
    return 0;
}

中序线索二叉树的构造和中序线索遍历化

#include<bits/stdc++.h>
using namespace std;
//中序线索二叉树的构造：利用中序遍历去遍历二叉树，构造一个前驱节点pre用于建立线索，如果一个节点不存在左子树
//则将pre指针作为它的前驱，如果pre的右子树为空，则将现在遍历的节点作为它的后继
//注意处理中序遍历的最后一个节点不存在右子树，将它的后继置为NULL
typedef struct ThreadNode{
    int val;
    ThreadNode* lchild;//左孩子
    ThreadNode* rchild;//右孩子
    int ltag;//用来标记是否存在左孩子   0表示存在 ， 1表示不存在
    int rtag;//用来标记是否存在右孩子
}ThreadNode,*ThreadTree;


// 中序遍历实现二叉树线索化的递归算法
void InThread(ThreadTree &p,ThreadTree &pre){//利用引用，要改变p和pre
    if(p!=NULL){
        InThread(p->lchild,pre);//pre表示中序遍历时，上一个刚刚访问的结点
        if(p->lchild==NULL){//左子树为空，建立前驱线索
            p->lchild=pre;
            p->ltag=1;
        }
        if(pre->rchild==NULL&&pre!=NULL){//如果pre的右子树为空，则将现在遍历的节点作为它的后继
            pre->rchild=p;
            pre->rtag=1;
        }
        pre=p;//标记当前结点为刚刚访问过的结点
        InThread(p->rchild,pre);//递归，遍历右子树
    }
}

// 通过中序遍历建立中序线索二叉树的主过程算法如下
void CreateInThread(ThreadTree T){
     ThreadTree pre=NULL;
     if(T!=NULL){
         InThread(T,pre);
         pre->rtag=1;
         pre->rchild=NULL;//处理中序遍历的最后一个节点不存在右子树，将它的后继置为NULL
     }
}

// 中序遍历算法
ThreadNode *FirstNode(ThreadNode *p){// 寻找中序线索二叉树的第一个结点
    while(p->ltag==0){
        p=p->lchild;// 最左下结点
    }
    return p;
}
ThreadNode *NextNode(ThreadNode *p){// 寻找当前结点的后继结点
    if(p->rtag==0){
        return FirstNode(p->rchild);// 右子树存在，寻找右子树的最左下结点
    }
    else
        return p->rchild; // 直接返回后继
}
// 线索化中序遍历
void InOrder(ThreadNode *T){
    for(ThreadNode p=FirstNode(T);p!=NULL;p=NextNode(p))
        visit(p);
}

int main()
{

    return 0;
}